
Weiter: Resonatoren mit sphärischen Spiegeln Oben: Resonatoren und ihre Lichtmoden Zurück: Resonatoren und ihre Lichtmoden Skript: PDF-Datei Übungen: Blätter
(Siehe Hecht, Optik [Hec, pp. 371]) (Siehe Yariv, Quantum Electronics [Yar75, pp. 99])
Zur Behandlung von Resonatoren verwenden wir die Matrixdarstellung der Lichtausbreitung paraxialer Strahlen in einer zylindersymmetrischen Anordnung. Die Lage des Lichtstrahls wird durch den Vektor
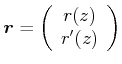 |
(6..1) |
| (6..2) |
![\includegraphics[width=0.8\textwidth]{Linsenresonator}](img1210.gif)
Linsenübertragungsstrecke als Modell für einen Laserresonator.
|
Der Strahl von der ![]() -ten zur
-ten zur ![]() -ten Linse ist durch
-ten Linse ist durch
![$\displaystyle \vec{r}_{aus} = \left[\begin{array}{cc} 1 & 0 -\frac{1}{f} & ...
...ay}{cc} 1 & d -\frac{1}{f} & -\frac{d}{f}+1 \end{array}\right]\vec{r}_{ein}$](img1212.gif) |
(6..3) |
Wir haben dann eine Lichtausbreitung in einem Resonator, wenn die Strahllage
nach der ![]() -ten Linse gleich wie nach der
-ten Linse gleich wie nach der ![]() -ten ist. Daraus folgt
-ten ist. Daraus folgt
![$\displaystyle \vec{r}_{aus} = \left[\begin{array}{cc} 1 & d -\frac{1}{f_1} ...
...cc} 1 & d -\frac{1}{f_2} & -\frac{d}{f_2}+1 \end{array}\right]\vec{r}_{ein}$](img1214.gif) |
(6..4) |
Ausmultipliziert erhalten wir
![$\displaystyle \vec{r}_{aus} = \left[\begin{array}{cc} 1-\frac{d}{f_2} & d\cdot\...
...d}{f_1}\right)\cdot\left(1-\frac{d}{f_2}\right) \end{array}\right]\vec{r}_{ein}$](img1215.gif) |
(6..5) |
Um eine Resonatormode zu bekommen muss
![]() sein.
Wir setzen
sein.
Wir setzen
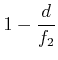 |
|||
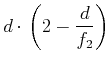 |
|||
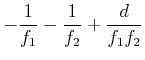 |
|||
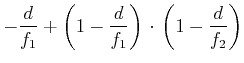 |
(6..6) |
Damit bekommen wir auch
Wir lösen die erste Gleichung nach ![]() auf und erhalten
auf und erhalten
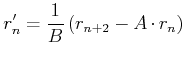 |
(6..8) |
Diese Gleichung schreiben wir um 2 verschoben hin und bekommen
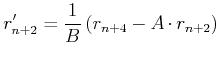 |
(6..9) |
Wir setzen diese Resultate in die zweite Gleichung (6.7) ein und erhalten
| (6..10) |
Durch ausrechnen erhält man, dass ![]() ist. Wenn wir
ist. Wenn wir
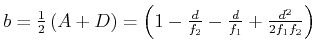 setzen, können wir schreiben
setzen, können wir schreiben
| (6..11) |
Diese Differenzengleichung ist formal äquivalent zu einer Differentialgleichung
vom Typ
![]() 6.1 Die Lösung der Differentialgleichung ist
6.1 Die Lösung der Differentialgleichung ist
![$ r(z)
= r(0)\exp\left[\pm i \sqrt{k} z\right]$](img1238.gif) . Deshalb setzen wir in die
Differenzengleichung den Ansatz
. Deshalb setzen wir in die
Differenzengleichung den Ansatz
![]() mit
mit
![]() ein und erhalten
ein und erhalten
| (6..12) |
Die Lösung ist
| (6..13) |
Mit
![]() und daraus
und daraus
![]() ist die obige
Gleichung erfüllt. Die allgemeine Lösung ist also
ist die obige
Gleichung erfüllt. Die allgemeine Lösung ist also
| (6..14) |
mit
![]() . Damit wir eine stabile Lösung haben, muss
. Damit wir eine stabile Lösung haben, muss
![]() reell sein. Daraus folgt
reell sein. Daraus folgt
| (6..15) |
Aus der Definition von ![]() folgt6.2
folgt6.2
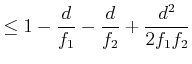 |
|||
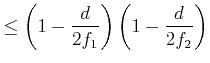 |
(6..16) |
Wenn wir die neuen normierten Koordinaten
![]() und
und
![]() einführen, heisst die Stabilitätsbedingung
einführen, heisst die Stabilitätsbedingung
| (6..17) |
![\includegraphics[width=0.6\textwidth]{resonator-stabil-2}](img1259.gif)
Stabilitätsdiagramm für Strahlführoptiken mit Linsen. Die gelbliche Farbe zeigt die instabilen Bereich, die türkis-Farbe die stabilen.
|
Das obige Stabilitätsdiagramm kann auch für Spiegel berechnet werden, indem man
![]() setzt, wobei
setzt, wobei ![]() der Krümmungsradius des Spiegels ist.
der Krümmungsradius des Spiegels ist.
![\includegraphics[width=0.6\textwidth]{resonator-stabil-3}](img1261.gif)
Das Stabilitätsdiagramm für Spiegelresonatoren.
|
|
|
Othmar Marti