
Weiter: Ebene Spiegel Oben: Geometrische Optik Zurück: Licht in der geometrischen Skript: PDF-Datei Übungen: Blätter
(Siehe Hecht, Optik [Hec, pp. 238]) (Siehe Tipler, Physik [TM04, pp. 1068]) (Siehe Pérez, Optik [Pér96, pp. 41])
|
|
![\includegraphics[width=0.6\textwidth]{brechung-glas-gekruemmt}](img66.gif)
Brechung von Licht an einer gekrümmten Glasoberfläche
|
Gleich wie mit Spiegeln können Abbildungen mit Linsen durchgeführt werden. Für
kleine Winkel gilt
![]() . Wir erhalten
. Wir erhalten
| (2..10) |
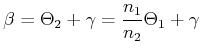 |
(2..11) |
| (2..12) |
| (2..13) |
Nach dem Strahlensatz ist
![]() . Der Abbildungsmassstab ist also
. Der Abbildungsmassstab ist also
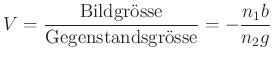 |
(2..15) |
(Siehe Hecht, Optik [Hec, pp. 242]) (Siehe Pérez, Optik [Pér96, pp. 106]) (Siehe Tipler, Physik [TM04, pp. 1071])
|
|
![\includegraphics[width=0.6\textwidth]{brechung-duenne-linse}](img84.gif)
|
Wir betrachten eine dünne Linse, das
heisst, dass wir die Dicke des Glases vernachlässigen. Die Linsenoberflächen
sollen die Krümmungsradien ![]() und
und ![]() (rechts) haben. Die Linse
mit dem Brechungsindex
(rechts) haben. Die Linse
mit dem Brechungsindex ![]() ist in Luft (Brechungsindex
ist in Luft (Brechungsindex ![]() ).
Ein Gegenstand befindet sich im Abstand
).
Ein Gegenstand befindet sich im Abstand ![]() links vor der ersten Ebene, und
damit auch im Abstand
links vor der ersten Ebene, und
damit auch im Abstand ![]() vor der Mittelebene. Die Bildweite
vor der Mittelebene. Die Bildweite ![]() aufgrund der ersten Oberfläche nach wird Gleichung (2.14)
mit
aufgrund der ersten Oberfläche nach wird Gleichung (2.14)
mit
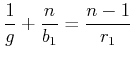 |
(2..16) |
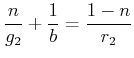 |
(2..17) |
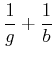 |
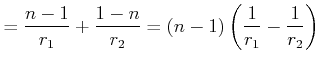 |
|
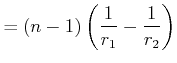 |
(2..18) |
Abbildungsgleichung
|
|
|
![\includegraphics[width=0.8\textwidth]{bessel}](img101.gif)
Die zwei Positionen einer Linse, bei denen eine scharfe Abbildung
erreicht wird.
|
Zur Berechnung verwenden wir die Abbildungsgleichung
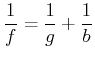 |
(2..20) |
| (2..21) |
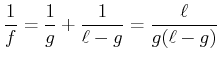 |
(2..22) |
| (2..23) | ||
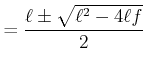 |
(2..24) | |
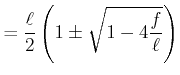 |
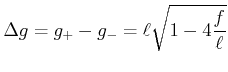 |
(2..25) |
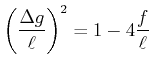 |
(2..26) |
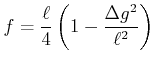 |
(2..27) |
![\includegraphics[width=0.6\textwidth]{Wellen-und-Linsen}](img115.gif)
|
Licht breitet sich in einem optisch dichteren Medium langsamer aus als im dünneren. Bei einer Konvexlinse treffen die achsennahen Lichtstrahlen eher auf das Glas als die achsenferneren. Diese überholen deshalb die achsennahen Lichtstrahlen. Im Wellenbild bedeutet dies, dass ebene Wellen zu konzentrisch auf einen Punkt zulaufenden Wellen werden: die Linse fokussiert.
![\includegraphics[width=0.6\textwidth]{zerstreuungslinse}](img116.gif)
Zerstreuungslinse
|
Bei einer Zerstreuungslinse sind die Oberflächen konkav gekrümmt. Die Krümmungsradien sind negativ. Eine Konkavlinse (Zerstreuungslinse) wirkt wie ein Konvexspiegel.
(Siehe Hecht, Optik [Hec, pp. 250]) (Siehe Pérez, Optik [Pér96, pp. 107]) (Siehe Tipler, Physik [TM04, pp. 1075])
Bei einer Linse gelten die folgenden Regeln zur Konstruktion der Bilder:
![\includegraphics[width=0.8\textwidth]{linsenabbildung}](img117.gif)
Abbildung bei einer Konvexlinse
|
Die Konstruktion der Abbildung bei einer Konvexlinse ist in der obigen
Abbildung gezeigt. ![]() ist die Gegenstandsweite,
ist die Gegenstandsweite, ![]() die Bildweite und
die Bildweite und
![]() die Brennweite. Die Vergrösserung ist:
die Brennweite. Die Vergrösserung ist:
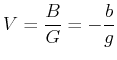 |
(2..28) |
![\includegraphics[width=0.8\textwidth]{Linsenabbildung-konkav}](img120.gif)
Abbildung bei einer Konkavlinse
|
Die Bildkonstruktion bei einer Konkavlinse verläuft analog zu der bei einer Konvexlinse.
(Siehe Hecht, Optik [Hec, pp. 363]) (Siehe Pérez, Optik [Pér96, pp. 100]) (Siehe Tipler, Physik [TM04, pp. 1077])
![\includegraphics[width=0.6\textwidth]{brechung-dicke-linse}](img121.gif)
|
Eine dicke Linse wird wie eine dünne berechnet, mit der Ausnahme, dass alle Messungen von Distanzen von den jeweiligen Hauptebenen aus gemacht werden müssen.
(Siehe Hecht, Optik [Hec, pp. 258]) (Siehe Pérez, Optik [Pér96, pp. 116]) (Siehe Tipler, Physik [TM04, pp. 1078])
![\includegraphics[width=0.8\textwidth]{doppellinse-1}](img122.gif)
Geometrie eines Doppellinsensystems
|
Bei mehreren Linsen berechnet man aus der Brennweite ![]() und der
Gegenstandsweite
und der
Gegenstandsweite ![]() die Bildweite
die Bildweite ![]() . Die Lage des Bildes gibt
die Gegenstandsweite
. Die Lage des Bildes gibt
die Gegenstandsweite ![]() der zweiten Linse. Mit der
Brennweite der zweiten Linse
der zweiten Linse. Mit der
Brennweite der zweiten Linse ![]() kann das Bild
kann das Bild ![]() berechnet werden. Zur Berechnung benötigen wir noch den Abstand der Linsen
berechnet werden. Zur Berechnung benötigen wir noch den Abstand der Linsen
![]() . Die Gegenstandsweite der zweiten Linse ist
. Die Gegenstandsweite der zweiten Linse ist
![]() .
.
Aus der Abbildungsgleichung erhalten wir
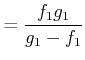 |
(2..29) | |
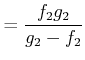 |
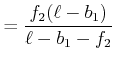 |
(2..30) | |
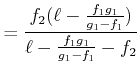 |
||
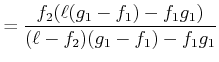 |
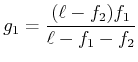 |
(2..31) |
Beispiel
![\includegraphics[width=0.7\textwidth]{doppellinse}](img148.gif)
Die Position des Bildes für verschiedene
|
Othmar Marti