



Next: Zusammenfassung: Ströme
Up: Elektrische Ströme
Previous: Hall-Effekt
(Siehe Leisi, Klassische Physik II[Lei98, 128])
Wir betrachten die Situation im Bild zum Halleffekt, nun aber vom Ruhesystem der Platte
aus. Hier haben die Elektronen keine Geschwindigkeit: es gibt keine Lorentzkraft.
|
Bewegte Magnetfelder und elektrische Felder.
|
Die obige Abbildung zeigt homogene Magnetfelder und elektrische Felder. Sie werden erzeugt, indem zwei
parallele Platten positiv beziehungsweise negativ geladen sind. Wenn die Platten mit der Geschwindigkeit
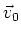 bewegt werden ergibt sich auch ein Magnetfeld.
bewegt werden ergibt sich auch ein Magnetfeld.
Das elektrische Feld beider Platten im Bezugssystem 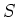 ist
ist
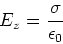 |
(3.136) |
wenn 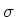 die Ladungsdichte in diesem Bezugssystem ist. Das Magnetfeld ist
die Ladungsdichte in diesem Bezugssystem ist. Das Magnetfeld ist
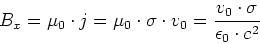 |
(3.137) |
Die entsprechenden Felder im Bezugssystem 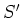 müssen nun berechnet werden. Auch in
müssen nun berechnet werden. Auch in 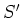 sind die Platten
homogen geladen. Also haben wir
sind die Platten
homogen geladen. Also haben wir
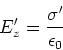 |
(3.138) |
und
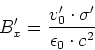 |
(3.139) |
Wir brauchen die Transformationsgesetze für 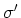 und
und 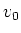
wenn 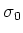 das Ruhesystem der Ladungen und
das Ruhesystem der Ladungen und
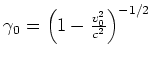 ist. Wir
bekommen
ist. Wir
bekommen
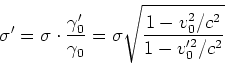 |
(3.141) |
und damit
und damit
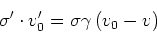 |
(3.143) |
Damit ist
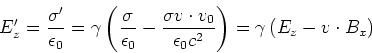 |
(3.144) |
und
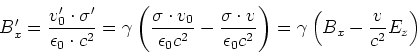 |
(3.145) |
Damit sind die transversalen Felder 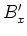 und
und 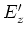 in
in 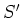 Linearkombinationen der Felder
Linearkombinationen der Felder 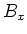 und
und 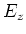 in
in 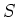 .
.
Die Transformationseigenschaften von 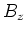 und
und 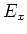 erhält man, indem man die obige Anordnung um
erhält man, indem man die obige Anordnung um 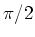 um
die
um
die 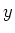 -Achse dreht. Dann gehen
-Achse dreht. Dann gehen
über. Die Transformationsgleichungen sind dann
Skizze zur Transformation eines longitudinale 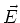 -Feldes (links) und des -Feldes (links) und des 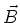 -Feldes
(rechts). -Feldes
(rechts).
|
Die Transformation des longitudinalen 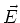 -Feldes ergibt sich aus der Erkenntnis, dass transversal zur
Geschwindigkeit keine Längenkontraktion auftritt und dass das Elektrische Feld eines
Plattenkondensators3.6nicht vom Plattenabstand abhängt. Also ist
-Feldes ergibt sich aus der Erkenntnis, dass transversal zur
Geschwindigkeit keine Längenkontraktion auftritt und dass das Elektrische Feld eines
Plattenkondensators3.6nicht vom Plattenabstand abhängt. Also ist
Also ist auch
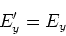 |
(3.149) |
Die Transformationseigenschaften des Magnetfeldes können mit der in der obigen Abbildung rechts angedeuteten
Spule berechnet werden. Das Magnetfeld in der Spule ist
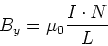 |
(3.150) |
wobei 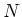 die Anzahl Windungen und
die Anzahl Windungen und 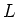 die Länge der Spule ist. Wir machen dabei die Annahme, dass die Spule
sehr lang im Vergleich zum Durchmesser sei. Mit
die Länge der Spule ist. Wir machen dabei die Annahme, dass die Spule
sehr lang im Vergleich zum Durchmesser sei. Mit 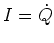 ist
ist
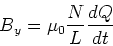 |
(3.151) |
Die Anzahl Windungen 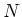 und die Ladung sind relativistisch invariant. Das transformierte Feld ist dann
und die Ladung sind relativistisch invariant. Das transformierte Feld ist dann
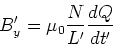 |
(3.152) |
Mit der Längenkontraktion 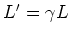 und der Zeitdilatation
und der Zeitdilatation
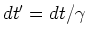 folgt, dass sich die
relativistischen Effekte kompensieren und damit
folgt, dass sich die
relativistischen Effekte kompensieren und damit
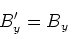 |
(3.153) |
ist.
![\framebox[0.9\textwidth]{\begin{minipage}{0.9\textwidth}\large\textcolor{red}{Be...
...\gamma\left(B_z+ \frac{v}{c^2}E_x\right)\nonumber
\end{eqnarray}}\end{minipage}}](img915.gif)




Next: Zusammenfassung: Ströme
Up: Elektrische Ströme
Previous: Hall-Effekt
Othmar Marti
Experimentelle Physik
Universiät Ulm
![\includegraphics[width=0.7\textwidth]{strom-015.eps}](img859.gif)
![]() bewegt werden ergibt sich auch ein Magnetfeld.
bewegt werden ergibt sich auch ein Magnetfeld.
![]() ist
ist
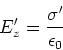
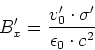
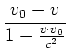
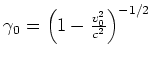 ist. Wir
bekommen
ist. Wir
bekommen
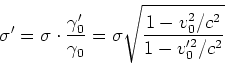
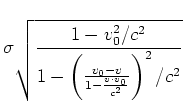
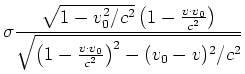
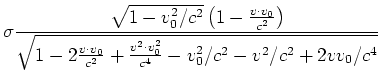
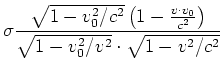
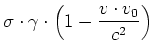
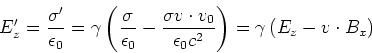
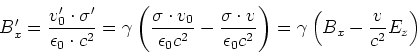
![]() und
und ![]() erhält man, indem man die obige Anordnung um
erhält man, indem man die obige Anordnung um ![]() um
die
um
die ![]() -Achse dreht. Dann gehen
-Achse dreht. Dann gehen
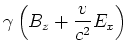
![\includegraphics[width=0.7\textwidth]{strom-016.eps}](img900.gif)
![]() -Feldes ergibt sich aus der Erkenntnis, dass transversal zur
Geschwindigkeit keine Längenkontraktion auftritt und dass das Elektrische Feld eines
Plattenkondensators3.6nicht vom Plattenabstand abhängt. Also ist
-Feldes ergibt sich aus der Erkenntnis, dass transversal zur
Geschwindigkeit keine Längenkontraktion auftritt und dass das Elektrische Feld eines
Plattenkondensators3.6nicht vom Plattenabstand abhängt. Also ist