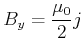




Next: Quellenfreiheit
Up: Eigenschaften des B-Feldes
Previous: Eigenschaften des B-Feldes
Contents
Index
| Dieser Stoff wurde am 13. 1. 2005
behandelt |
(Siehe Leisi, Klassische Physik II [Lei98, pp. 104])
Beim unendlich ausgedehnten geraden Leiter war das durch einen Strom 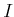 erzeugte Magnetfeld durch kreisförmige
Magnetfeldlinien mit der Stärke
erzeugte Magnetfeld durch kreisförmige
Magnetfeldlinien mit der Stärke
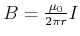 charakterisiert, wobei das
charakterisiert, wobei das 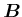 -Feld tangential
zu den Kreisen liegt. Das Linienintegral entlang der Feldlinien, also entlang des Kreises
-Feld tangential
zu den Kreisen liegt. Das Linienintegral entlang der Feldlinien, also entlang des Kreises 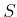 , ergibt
, ergibt
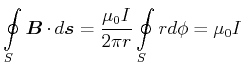 |
(3.255) |
Dieses Linienintegral ist unabhängig von 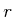 . Die Behauptung ist, das die obige Gleichung, ein einfacher Fall des
Ampèreschen Durchflutungsgesetzes, allgemeingültig ist.
. Die Behauptung ist, das die obige Gleichung, ein einfacher Fall des
Ampèreschen Durchflutungsgesetzes, allgemeingültig ist.
Ampèresches Durchflutungsgesetz
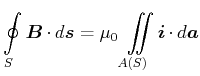 |
(3.256) |
|
Der Beweis geht in mehreren Schritten:
- Eine beliebige Kurve
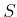 um einen geraden Leiter
um einen geraden Leiter

![\includegraphics[width=0.5\textwidth]{strom-009}](img933.gif)
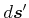 ist die Projektion des Weglängenelementes
ist die Projektion des Weglängenelementes 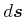 auf der Kurve
auf der Kurve 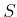 auf die in der
auf die in der
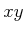 -Ebene liegende Projektion der Kurve
-Ebene liegende Projektion der Kurve 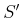 . Es ist
da
. Es ist
da
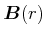 keine Komponente in die
keine Komponente in die 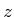 -Richtung hat. Es ist
und damit
-Richtung hat. Es ist
und damit
- Eine beliebige Kurve
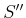 , die den Leiter nicht umschliesst
, die den Leiter nicht umschliesst
- Es ist
Das bedeutet, dass Ströme durch Leiter, die nicht vom Integrationsweg
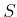 umschlossen werden, keinen
Beitrag zum Integral geben.
umschlossen werden, keinen
Beitrag zum Integral geben.
- Eine beliebige Kurve
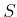 um eine beliebige Stromverteilung
um eine beliebige Stromverteilung
- Wir betrachten viele Ströme
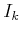 , die
von der Integrationskurve
, die
von der Integrationskurve 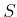 umschlossen werden. Wegen der Linearität des Problems gilt
wobei diejenigen Ströme, die mit dem Umlaufsinn von
umschlossen werden. Wegen der Linearität des Problems gilt
wobei diejenigen Ströme, die mit dem Umlaufsinn von 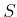 eine Rechtsschraube bilden, positiv zu zählen sind.
eine Rechtsschraube bilden, positiv zu zählen sind.
Beispiel
Ein zylindrischer Leiter mit dem Radius 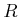 soll homogen vom Strom
soll homogen vom Strom 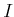 durchflossen werden. Aus Symmetriegründen
sind die Magnetfeldlinien konzentrische Kreise um den Leiter. Ausserhalb des Leiters (
durchflossen werden. Aus Symmetriegründen
sind die Magnetfeldlinien konzentrische Kreise um den Leiter. Ausserhalb des Leiters (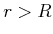 ) haben wir
) haben wir
Innerhalb des Leiters (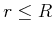 ) gilt
) gilt
|
Tangentiales Magnetfeld eines ausgedehnten, unendlich langen Linienstromes.
|
Mit dem Stokeschen Satz (Gleichung (A.43) ) kann man die Integralform des Ampèreschen Gesetzes umschreiben
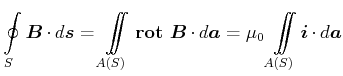 |
(3.257) |
Da diese Gleichungen für alle Integrationsflächen 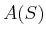 gelten müssen, muss auch die differentielle Form des
Ampèreschen Gesetzes gelten
gelten müssen, muss auch die differentielle Form des
Ampèreschen Gesetzes gelten
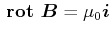 |
(3.258) |
|
Beispiel: homogene Stromverteilung in einem unendlich ausgedehnten Leiter
|
Magnetfeld einer homogenen Stromverteilung in einer dünnen Platte. Links: die Geometrie zur Berechnung,
Mitte: das Magnetfeld eines homogenen Stromflusses und Rechts: das Magnetfeld zweier antiparallel von Strom
durchflossener Platten.
|
Wir definieren eine lineare Stromdichte
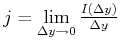 .
Das Stromfeld können wir uns als Parallelschaltung vieler linearer Leiter vorstellen. Aus dem
Superpositionsprinzip folgt, dass
.
Das Stromfeld können wir uns als Parallelschaltung vieler linearer Leiter vorstellen. Aus dem
Superpositionsprinzip folgt, dass
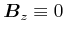 |
(3.259) |
Das resultierende Feld dieser Superposition muss in der 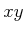 -Ebene liegen. Auf den beiden Seiten senkrecht zur
Platte finden sich immer zwei Stromfäden, die die
-Ebene liegen. Auf den beiden Seiten senkrecht zur
Platte finden sich immer zwei Stromfäden, die die 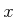 -Komponente kompensieren. Wenn wir später das Ampèresche
Gesetz auf diese beiden Seiten anwenden, gibt es keine Komponente von
-Komponente kompensieren. Wenn wir später das Ampèresche
Gesetz auf diese beiden Seiten anwenden, gibt es keine Komponente von  parallel zur Seite: dieser Teil
des Linienintegrals ist null.
parallel zur Seite: dieser Teil
des Linienintegrals ist null.
Wir betrachten weiter das Feld
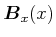 und
und
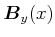 im Abstand
im Abstand 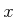 von der Platte. Wir werden zwei
Symmetrieoperationen an:
von der Platte. Wir werden zwei
Symmetrieoperationen an:
- Wir drehen die Platte um
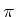 um die
um die 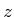 -Achse. Die neue Situation (Ströme) ist identisch mit der
Ursprungssituation. Deshalb muss
sein.
-Achse. Die neue Situation (Ströme) ist identisch mit der
Ursprungssituation. Deshalb muss
sein.
- Wir drehen die Platte um
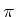 um die
um die 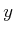 -Achse und drehen gleichzeitig die Flussrichtung des
Stromes um
-Achse und drehen gleichzeitig die Flussrichtung des
Stromes um
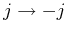 . Die Endsituation ist ununterscheidbar von der am Anfang. Also gilt auch
und
.
. Die Endsituation ist ununterscheidbar von der am Anfang. Also gilt auch
und
.
Mit den beiden Symmetrieüberlegungen folgt:
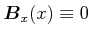 |
(3.260) |
Um 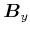 zu bestimmen, nehmen wir an, dass unser Integrationspfad
zu bestimmen, nehmen wir an, dass unser Integrationspfad 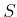 symmetrisch bezüglich der Platte ist.
Das Ampèresche Gesetz sagt
symmetrisch bezüglich der Platte ist.
Das Ampèresche Gesetz sagt
Das Resultat ist unabhängig von 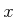 und homogen im Raum. Die Magnetfeldlinien sind parallel zur Platte und links
und rechts antiparallel (siehe Abbildung oben Mitte).
und homogen im Raum. Die Magnetfeldlinien sind parallel zur Platte und links
und rechts antiparallel (siehe Abbildung oben Mitte).
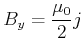 |
(3.261) |
Bei zwei antiparallel von Strom durchflossenen Platten ist das Magnetfeld auf den Raum zwischen den Platten
beschränkt.
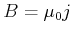 |
(3.262) |
Anwendungsbeispiele: Streifenleiter, Koaxialkabel





Next: Quellenfreiheit
Up: Eigenschaften des B-Feldes
Previous: Eigenschaften des B-Feldes
Contents
Index
Marti
2011-10-13

![]() erzeugte Magnetfeld durch kreisförmige
Magnetfeldlinien mit der Stärke
erzeugte Magnetfeld durch kreisförmige
Magnetfeldlinien mit der Stärke
![]() charakterisiert, wobei das
charakterisiert, wobei das ![]() -Feld tangential
zu den Kreisen liegt. Das Linienintegral entlang der Feldlinien, also entlang des Kreises
-Feld tangential
zu den Kreisen liegt. Das Linienintegral entlang der Feldlinien, also entlang des Kreises ![]() , ergibt
, ergibt
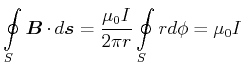
![\includegraphics[width=0.5\textwidth]{strom-009}](img933.gif)
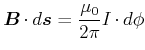
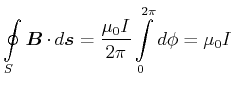
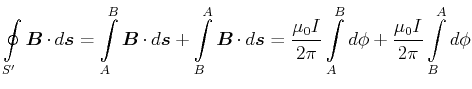
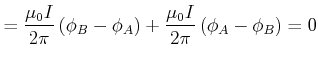
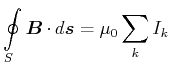
![]() soll homogen vom Strom
soll homogen vom Strom ![]() durchflossen werden. Aus Symmetriegründen
sind die Magnetfeldlinien konzentrische Kreise um den Leiter. Ausserhalb des Leiters (
durchflossen werden. Aus Symmetriegründen
sind die Magnetfeldlinien konzentrische Kreise um den Leiter. Ausserhalb des Leiters (![]() ) haben wir
) haben wir
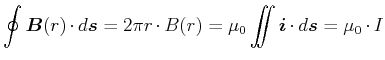
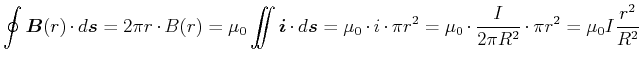
![\includegraphics[width=0.6\textwidth]{B_linienstrom}](img947.gif)
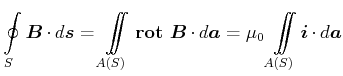
![\includegraphics[width=0.9\textwidth]{strom-014}](img951.gif)
![]() .
Das Stromfeld können wir uns als Parallelschaltung vieler linearer Leiter vorstellen. Aus dem
Superpositionsprinzip folgt, dass
.
Das Stromfeld können wir uns als Parallelschaltung vieler linearer Leiter vorstellen. Aus dem
Superpositionsprinzip folgt, dass
![]() und
und
![]() im Abstand
im Abstand ![]() von der Platte. Wir werden zwei
Symmetrieoperationen an:
von der Platte. Wir werden zwei
Symmetrieoperationen an:
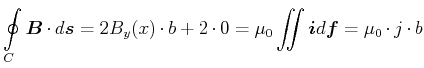
![]() und homogen im Raum. Die Magnetfeldlinien sind parallel zur Platte und links
und rechts antiparallel (siehe Abbildung oben Mitte).
und homogen im Raum. Die Magnetfeldlinien sind parallel zur Platte und links
und rechts antiparallel (siehe Abbildung oben Mitte).