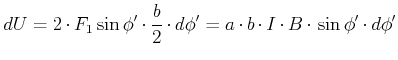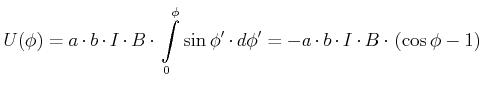




Next: Das Ampèresche Durchflutungsgesetz
Up: Elektrische Ströme
Previous: Relativistische Berechnung
Contents
Index
| Dieser Stoff wurde am 23. 12. 2004
behandelt |
(Siehe Leisi, Klassische Physik II [Lei98, pp. 98])
Um nicht immer die Lorentz-Transformation ausrechnen zu müssen , führen wir die magnetische
Feldstärke oder die magnetische Induktion
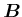 ein. Ein magnetisches Feld lenkt Elektronen ab. Wie wir schon früher gesehen haben, ist eine Bewegung
der Ladungsträger für die magnetische Kraft notwendig. Wird das Magnetfeld der Helmholtzspulen so
gedreht, dass es parallel zur Bewegungsrichtung der Elektronen liegt, verschwindet die Magnetkraft. Das
folgende Kraftgesetz
ein. Ein magnetisches Feld lenkt Elektronen ab. Wie wir schon früher gesehen haben, ist eine Bewegung
der Ladungsträger für die magnetische Kraft notwendig. Wird das Magnetfeld der Helmholtzspulen so
gedreht, dass es parallel zur Bewegungsrichtung der Elektronen liegt, verschwindet die Magnetkraft. Das
folgende Kraftgesetz
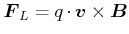 |
(3.232) |
|
beschreibt die magnetischen Kräfte auf Elektronen. Die Kraft 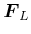 heisst Lorentz-Kraft.
heisst Lorentz-Kraft.
Durch den Vergleich von Gleichung (3.98) und Gleichung (3.96) kann man für die magnetische Feldstärke einer
linienförmigen Stromverteilung schreiben
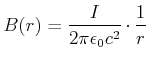 |
(3.233) |
Die Induktionskonstante
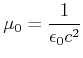 |
(3.234) |
ermöglicht es Gleichung (3.99) kompakter zu schreiben
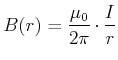 |
(3.235) |
|
Lage der magnetischen Induktion zum Strom und zur Geschwindigkeit der Ladung.
|
Die magnetische Induktion 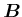 bildet eine Rechtsschraube um den Strom bildet eine Rechtsschraube um den Strom 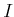 (Daumen in
Stromrichtung, Finger zeigen in die Richtung der magnetischen Induktion). (Daumen in
Stromrichtung, Finger zeigen in die Richtung der magnetischen Induktion).
|
|
Die magnetische Induktion eines geraden, unendlich ausgedehnten Stromes bildet Feldlinien, die
kreisförmig in einer Ebene senkrecht zum Strom liegen. Der Mittelpunkt der kreisförmigen Feldlinien ist der
Strom.
|
Die Kraft zwischen zwei stromdurchflossenen Leitern kann neu berechnet werden. Mit
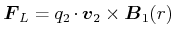 |
(3.236) |
wobei 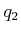 eine Ladung im Leiter 2 ist, und mit
eine Ladung im Leiter 2 ist, und mit 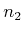 der Ladungsträgerdichte im Leiter 2,
der Ladungsträgerdichte im Leiter 2, 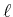 die
betrachtete Länge,
die
betrachtete Länge, 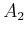 der Querschnitt des Leiters und
der Querschnitt des Leiters und
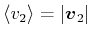 , bekommt man
, bekommt man
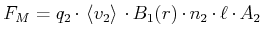 |
(3.237) |
Der Strom im Leiter 2 ist nun aber
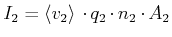 |
(3.238) |
Damit ist
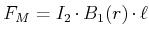 |
(3.239) |
Wenn wir Gleichung (3.101) einsetzen, bekommen wir
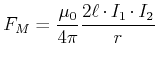 |
(3.240) |
Diese Gleichung wird zur Definition der Einheit der magnetischen Induktion im SI-System verwendet.
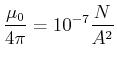 |
(3.241) |
|
Die Einheit der magnetischen Induktion ist
![$\displaystyle [B] = Tesla = T = \frac{N\cdot s}{C \cdot m} = \frac{N}{A m}= \frac{V\cdot s}{m^2}$](img900.gif) |
(3.242) |
- Die gesamte Kraft einer bewegten Ladung
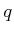 in einer beliebigen Ladungs- und Stromverteilung ist
in einer beliebigen Ladungs- und Stromverteilung ist
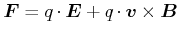 |
(3.243) |
Dies ist das Kraftgesetz der Elektrodynamik
- Das magnetische Feld ist kein fundamentales Feld, sondern eine relativistische Korrektur zu dem
elektrostatischen Feld.
| Dieser Stoff wurde am 13. 1. 2005
behandelt |
![\includegraphics[height=8mm]{icon-mat}](img217.gif) |
Materialien
Folien zur Vorlesung vom 13. 01. 2005: PDF
|
Die Kraft auf einen stromdurchflossenen Leiter in einem beliebigen Magnetfeld kann mit dem Gesetz von
Biot-Savart berechnet werden.
|
Berechnung der Kraft auf ein Leiterelement.
|
Der Betrag des Vektors 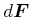 , der senkrecht auf
, der senkrecht auf
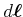 und senkrecht auf
und senkrecht auf 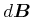 steht, ist
steht, ist
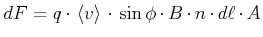 |
(3.244) |
wobei 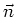 die Dichte der Ladungsträger und
die Dichte der Ladungsträger und 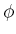 der Winkel zwischen
der Winkel zwischen 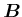 und
und
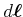 ist. Mit der Stromdichte
ist. Mit der Stromdichte
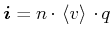 erhalten wir
erhalten wir
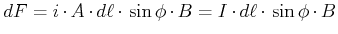 |
(3.245) |
Die vektorielle Schreibweise der Biot-Savart-Kraft ist
demnach
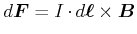 |
(3.246) |
|
Beispiele
- Die Kraft für eine beliebig geformte geschlossene Leiterschleife in einem homogenen Magnetfeld ist
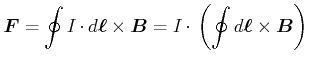 |
(3.247) |
Da das Linienintegral
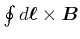 über eine geschlossene Schleife null ist (die positiven und die negativen Anteile heben
sich auf) ist
über eine geschlossene Schleife null ist (die positiven und die negativen Anteile heben
sich auf) ist
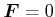 .
.
- Das Drehmoment auf eine Leiterschlaufe in einem homogenen Magnetfeld kann durch summieren der
Kraftanteile auf die vier Segmente berechnet werden.
|
Drehmoment auf eine Leiterschleife im homogenen Magnetfeld
|
Bezüglich 0 ist die Situation symmetrisch. Die in der Zeichnung vertikalen Leiterelemente liefern
kollineare sich aufhebende Kräfte. Die horizontalen Segmente ergeben das Drehmoment
Das gesamte Drehmoment ist
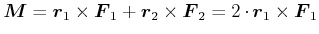 |
(3.249) |
Das Drehmoment 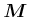 liegt in der Ebene der Leiterschlaufe. Wenn
liegt in der Ebene der Leiterschlaufe. Wenn 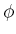 der Winkel zwischen der
Normalen auf die Ebene der Leiterschlaufe und
der Winkel zwischen der
Normalen auf die Ebene der Leiterschlaufe und 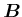 ist, gilt mit
ist, gilt mit
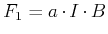 :
:
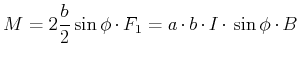 |
(3.250) |
Wir definieren das magnetische Moment 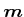 so, dass es senkrecht auf die Ebene der Leiterschlaufe steht und dass
so, dass es senkrecht auf die Ebene der Leiterschlaufe steht und dass
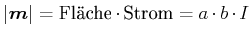 ist. Damit ist
ist. Damit ist
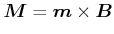 |
(3.251) |
Das Drehmoment auf eine Leiterschlaufe im homogenen Magnetfeld wird in
Drehspulinstrumenten, in Motoren oder bei der
Sichtbarmachung von Magnetfeldern mit Eisenfeilspänen verwendet.
- Die potentielle Energie einer um den Winkel
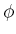 gegenüber dem Magnetfeld verdrehten
stromdurchflossenen Leiterschlaufe wird berechnet, indem man von
gegenüber dem Magnetfeld verdrehten
stromdurchflossenen Leiterschlaufe wird berechnet, indem man von 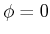 ausgeht und die Schlaufe
langsam zum Winkel
ausgeht und die Schlaufe
langsam zum Winkel 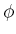 dreht. Die Arbeit, um von
dreht. Die Arbeit, um von 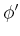 nach
nach
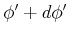 zu drehen ist
zu drehen ist
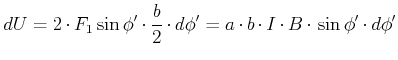 |
(3.252) |
Damit erhalten wir
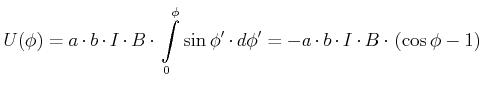 |
(3.253) |
Wenn wir
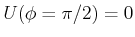 wählen haben wir
wählen haben wir
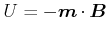 |
(3.254) |
Ein weiteres Beispiel einer Kraftwirkung auf Ladungen ist das Barlowsche Rad.
Subsections





Next: Das Ampèresche Durchflutungsgesetz
Up: Elektrische Ströme
Previous: Relativistische Berechnung
Contents
Index
Marti
2011-10-13

![]() ein. Ein magnetisches Feld lenkt Elektronen ab. Wie wir schon früher gesehen haben, ist eine Bewegung
der Ladungsträger für die magnetische Kraft notwendig. Wird das Magnetfeld der Helmholtzspulen so
gedreht, dass es parallel zur Bewegungsrichtung der Elektronen liegt, verschwindet die Magnetkraft. Das
folgende Kraftgesetz
ein. Ein magnetisches Feld lenkt Elektronen ab. Wie wir schon früher gesehen haben, ist eine Bewegung
der Ladungsträger für die magnetische Kraft notwendig. Wird das Magnetfeld der Helmholtzspulen so
gedreht, dass es parallel zur Bewegungsrichtung der Elektronen liegt, verschwindet die Magnetkraft. Das
folgende Kraftgesetz
![]() heisst Lorentz-Kraft.
heisst Lorentz-Kraft.
![\includegraphics[width=0.7\textwidth]{strom-006}](img889.gif)
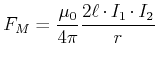
![$\displaystyle [B] = Tesla = T = \frac{N\cdot s}{C \cdot m} = \frac{N}{A m}= \frac{V\cdot s}{m^2}$](img900.gif)
![\includegraphics[width=0.7\textwidth]{strom-007}](img902.gif)
![]() , der senkrecht auf
, der senkrecht auf
![]() und senkrecht auf
und senkrecht auf ![]() steht, ist
steht, ist
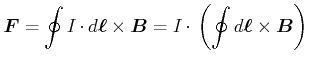
![\includegraphics[width=0.7\textwidth]{strom-008}](img913.gif)