
Wenn
![]() ein konstanter Geschwindigkeitsvektor ist und diese Grösse an einem mit der Geschwindigkeit
ein konstanter Geschwindigkeitsvektor ist und diese Grösse an einem mit der Geschwindigkeit ![]() bewegten Ort beobachtet wird, dann gilt (Siehe Jackson[Jac75, p212]):
bewegten Ort beobachtet wird, dann gilt (Siehe Jackson[Jac75, p212]):
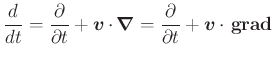 |
(A..562) |
wobei
![]() die totale Ableitung im raumfesten Koordinatensystem und
die totale Ableitung im raumfesten Koordinatensystem und
![]() die lokale, mitgeführte Ableitung ist. Mit Gleichung (A.32) kann man schreiben
die lokale, mitgeführte Ableitung ist. Mit Gleichung (A.32) kann man schreiben
| (A..563) |
oder
| (A..564) |
Nun ist
![]() . Weiter ist
. Weiter ist
![]() und
und
![]() , wobei
, wobei ![]() die 3 mal 3 Einheits-Diagonalmatrix ist. Damit haben wir ohne Einschränkung der Allgemeinheit
die 3 mal 3 Einheits-Diagonalmatrix ist. Damit haben wir ohne Einschränkung der Allgemeinheit
| (A..565) |
und
