
| Dieser Stoff wurde am 12. 4. 2005 behandelt |
| Dieser Stoff wurde am 12. 4. 2005 behandelt |
Wärmestrahlung ist eine Form elektromagnetischer Strahlung. Die Sonne versorgt so die Erde mit der notwendigen
Energie. Aus der Optik wissen wir, dass bei einem Strahlungsfluss ![]() auf eine Grenzfläche die folgende
Energiebilanz gilt:
auf eine Grenzfläche die folgende
Energiebilanz gilt:
| (3.22) |
| (3.23) |
Wenn man die Ausstrahlung einer schwarzen Fläche (
![]() ) mit
) mit ![]() beschreibt ist die Ausstrahlung einer
beliebigen Fläche durch
beschreibt ist die Ausstrahlung einer
beliebigen Fläche durch
| (3.24) |
Nehmen wir an, eine Fläche mit
![]() under Temperatur
under Temperatur ![]() strahle die Leistung
strahle die Leistung ![]() auf die zweite Fläche
mit der Temperatur
auf die zweite Fläche
mit der Temperatur ![]() . Gleichzeitig strahle die zweite Fläche mit
. Gleichzeitig strahle die zweite Fläche mit
![]() die Leistung
die Leistung ![]() auf die erste
Fläche. Beide Flächen sind im thermischen Gleichgewicht. Dann muss
auf die erste
Fläche. Beide Flächen sind im thermischen Gleichgewicht. Dann muss
| (3.26) |
|
|
|
|
|
|
| Dieser Stoff wurde am 12. 4. 2005 behandelt |
(Siehe Gerthsen, Physik [Mes04, pp. 573])
![\includegraphics[width=0.5\textwidth]{schwarzkoerper}](img190.gif)
|
Licht, das durch die kleine Öffnung in den Hohlraum des schwarzen Körpers eintritt, wird bei jeder Reflexion an der Oberfläche mit der Wahrscheinlichkeit
![]() absorbiert und mit der Wahrscheinlichkeit
absorbiert und mit der Wahrscheinlichkeit
![]() reflektiert. Nach
reflektiert. Nach ![]() Reflexionen ist die
verbleibende Intensität des Lichtstrahls auf
Reflexionen ist die
verbleibende Intensität des Lichtstrahls auf
![]() abgesunken, sie wird also beliebig klein. Das
heisst. der Absorptionsgrad der Öffnung in diesem Hohlraum ist
abgesunken, sie wird also beliebig klein. Das
heisst. der Absorptionsgrad der Öffnung in diesem Hohlraum ist
![]() .
.
Spektrale Grössen werden hier mit dem Subskript
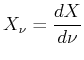
|
Wir definieren nun eine spektrale Energiedichte
![]() . Sie besteht aus dem Produkt aus der
Energiedichte
. Sie besteht aus dem Produkt aus der
Energiedichte
![]() und dem Frequenzband der Breite
und dem Frequenzband der Breite ![]() , das das Intervall
, das das Intervall
![]() beschreibt. Diese Energie
beschreibt. Diese Energie
![]() bewegt sich mit der Geschwindigkeit
bewegt sich mit der Geschwindigkeit ![]() durch den Raum und zu den
Wänden des Hohlraums. Eine ideale schwarze Wand absorbiert diese Energie
durch den Raum und zu den
Wänden des Hohlraums. Eine ideale schwarze Wand absorbiert diese Energie
![]() und emittiert nach
Kirchhoff gleichzeitig
und emittiert nach
Kirchhoff gleichzeitig
![]() . Im Gleichgewicht müssen sich die Absorption und die Emission die
Balance halten. Wir können also die spezifische Ausstrahlung durch die Energiedichte
. Im Gleichgewicht müssen sich die Absorption und die Emission die
Balance halten. Wir können also die spezifische Ausstrahlung durch die Energiedichte ![]() ausdrücken3.
ausdrücken3.
Die gemessene spektrale Energiedichte sieht wie in der Abbildung aus.
![\includegraphics[width=0.7\textwidth]{planck1}](img203.gif)
|
Wenn man gegen die Energiedichteverteilung gegen die Frequenz aufträgt, sieht das ganze so aus:
![\includegraphics[width=0.7\textwidth]{planck2}](img204.gif)
|
| Dieser Stoff wurde am 18. 4. 2005 behandelt |
|
|
Materialien
Folien zur Vorlesung am 18. 04. 2005 PDF Übungsblatt 02 vom 18. 04. 2005 (HTML oder PDF) |
|
|
|
|
Plancksches Wirkungsquantum
| (3.29) |
Eselsbrücke:
![]()
Reduziertes Wirkungsquantum
| (3.30) |
Eselsbrücke:
![]()
|
Quantenhypothese Einsteins
Atome, die die Energie |
Definitionen:
Wir nehmen das thermische Gleichgewicht an und verwenden deshalb die Boltzmann-Verteilung
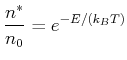 |
(3.31) |
Energieaustausch
![\includegraphics[width=0.4\textwidth]{anregungsschema}](img213.gif)
|
Zur Berechnung des Spektrums eines schwarzen Strahlers verwenden wir die Einsteinsche Formulierung mit Quanten.
Von Einstein stammt das Postulat der induzierten Emission. Planck hatte ursprünglich das Spektrum mit thermodynamischen Methoden berechnet, wobei ![]() das
Phasenraumvolumen war.
das
Phasenraumvolumen war.
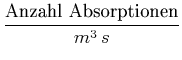 |
(3.32) | ||
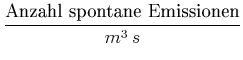 |
|||
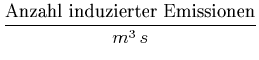 |
wobei ![]() der Einsteinkoeffizient der spontanen Emission,
der Einsteinkoeffizient der spontanen Emission, ![]() der
Einsteinkoeffizient der Absorption und
der
Einsteinkoeffizient der Absorption und ![]() der Einsteinkoeffizient der induzierten
Emission.
der Einsteinkoeffizient der induzierten
Emission.
Im Gleichgewicht gibt es gleich viele Emissionen wie Absorptionen.
| (3.33) |
Da die induzierte Emission der Umkehrprozess der Absorption ist, muss
| (3.34) |
sein.
Umformung
| (3.35) |
Energiedichte
Infinitesimal geschrieben bekommen wir
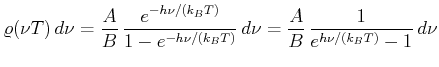 |
(3.36) |
![]() berechnet man aus der Modendichte des Hohlraumes
berechnet man aus der Modendichte des Hohlraumes
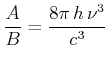 |
(3.37) |
Grenzfall
![]()
dann gilt
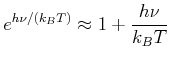
Für
![]() ist
ist
![\includegraphics[width=0.7\textwidth]{planck-wien}](img238.gif)
|
Kosmische Energiedichteverteilung
![\includegraphics[width=0.7\textwidth]{planck-hg}](img240.gif)
|
| Dieser Stoff wurde am 18. 4. 2005 behandelt |
Zur Berechnung des Maximums substituieren wir in Gleichung (3.23)
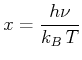
und
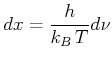
und vernachlässigen die Vorfaktoren.
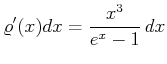
Maximum
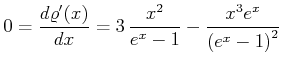
und
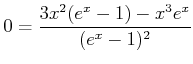
oder
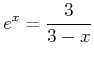
Die Lösung der Gleichung ist
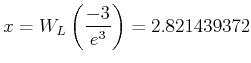
wobei ![]() Lambert's W-Funktion
ist.
Lambert's W-Funktion
ist.
Lage des Maximums in der Planckschen Strahlungsformel in Gleichung (3.23)
![\includegraphics[width=0.7\textwidth]{Wien}](img253.gif)
|
Die Energiedichten bei den Emissionsmaxima sind
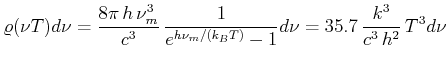 |
(3.42) |
![\includegraphics[width=0.7\textwidth]{Wien-energie}](img255.gif)
|
| Dieser Stoff wurde am 18. 4. 2005 behandelt |
|
|
|
|
Spezifische Ausstrahlung nach Gleichung (3.12) senkrecht zur Oberfläche
Richtungsabhängige Abstrahlung (![]() Winkel zur Normalen)
Winkel zur Normalen)
Mittelung über Halbraum
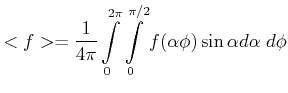
und über Frequenz
![$\displaystyle R(T) = \frac{1}{4\pi}\int\limits_0^{2\pi}\int\limits_0^{\pi/2}\le...
...0^\infty c\cdot \varrho(\nu,T) d\nu \cos\alpha\right]\sin\alpha d\alpha\;d\phi$](img259.gif) |
(3.43) |
Die Integrale sind voneinander unabhängig.
Mit
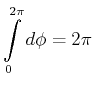
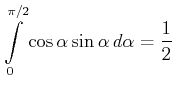
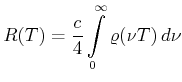 |
(3.44) |
Das Integral ergibt
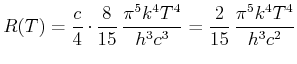 |
(3.45) |
Stefan-Boltzmann-Konstante
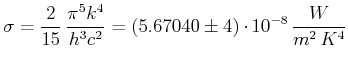 |
(3.46) |
![]() ist die in den Halbraum abgestrahlte Leistung bei der Temperatur
ist die in den Halbraum abgestrahlte Leistung bei der Temperatur ![]() .
.
![\includegraphics[width=0.7\textwidth]{stefan-boltzmann}](img266.gif)
|
| Dieser Stoff wurde am 19. 4. 2005 behandelt |
|
|
Materialien
Folien zur Vorlesung am 19. 04. 2005 PDF |
![\includegraphics[width=0.7\textwidth]{auge}](img267.gif)
|
| Dieser Stoff wurde am 19. 4. 2005 behandelt |
![\includegraphics[width=0.7\textwidth]{planck-treibhaus}](img268.gif)
|
