
Weiter: Teilchensysteme Oben: Mechanik in drei Dimensionen Zurück: Erhaltungssätze und Erhaltungsgrössen Skript: PDF-Datei Übungen: Blätter ILIAS: Materialien Korrekturen
Die Dynamik stellt die Frage nach der Ursache der Bewegung. In diesem Abschnitt werden wir zeigen, dass Bewegung wird durch Kräfte hervorgerufen wird.
auch genannt 4. Newtonsches Gesetz
| Kräfte sind Vektoren |
![\includegraphics[width=0.7\textwidth]{mechanik-015}](img823.gif)
Reibung
|
Eine Kraft, die am Punkt ![]() angreift, verhält sich wie ein ortsgebundener Vektor.
angreift, verhält sich wie ein ortsgebundener Vektor.
![\begin{displaymath}
\left.
\begin{array}[c]{cc}
\text{Angriffspunkt} & P\\
\te...
... & \vec{e=}\frac{\vec{F}}{F}
\end{array}\right\} \text{Kraft!}
\end{displaymath}](img824.gif)
|
|
Addition von Kräften
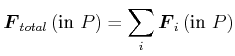 |
(4.207) |
![]() Nur Kräfte, die an ein und demselben Punkt
Nur Kräfte, die an ein und demselben Punkt ![]() angreifen können addiert werden.
angreifen können addiert werden.
Beispiel:
![\includegraphics[width=0.2\textwidth]{mechanik-016}](img827.gif)
Grafische Addition von Kräften
|
Die Kräfte, die im Punkt ![]() angreifen sind im Gleichgewicht, wenn ihre Summe 0 ist.
angreifen sind im Gleichgewicht, wenn ihre Summe 0 ist.
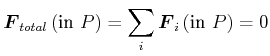 |
(4.208) |
Beispiel
![\includegraphics[width=0.2\textwidth]{mechanik-017}](img829.gif)
|
Zerlegung von Kräften
Beispiel: Welche Kräfte wirken auf einen Kranarm?
![\includegraphics[width=0.4\textwidth]{mechanik-018}](img831.gif)
|
|
|
|
|
|
|
auch genannt das 3. Newtonsches Gesetz
Übt der Körper ![]() die Kraft
die Kraft
![]() auf der Körper
auf der Körper ![]() aus, so übt der Körper
aus, so übt der Körper ![]() die
Kraft
die
Kraft
![]() auf den Körper
auf den Körper ![]() aus.
aus.
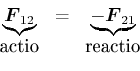 |
(4.209) |
![\includegraphics[width=0.5\textwidth]{mechanik-020}](img840.gif)
|
![]() ist die Reaktion der Feder auf die angelegte Kraft.
ist die Reaktion der Feder auf die angelegte Kraft.
auch genannt 2. Newtonsches Gesetz
Eine bewegte Masse kann durch ihren Impuls charakterisiert werden.
| (4.210) |
Einheit des Impulses:
![]()
Dabei ist ![]() die träge Masse (im Gegensatz zur schweren Masse)
die träge Masse (im Gegensatz zur schweren Masse)
Das 2. Newtonsche Gesetz lautet
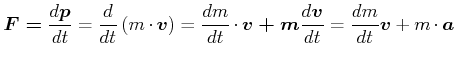 |
(4.211) |
Die Kraft entspricht also einer Impulsänderung.
Bei einer Bewegung ohne äussere Kraft gilt:
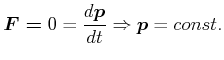 |
(4.212) |
Ein konstanter Impuls heisst, dass entweder die Geschwindigkeit ![]() mit abnehmender
Masse zunimmt, oder, im Spezialfall dass
mit abnehmender
Masse zunimmt, oder, im Spezialfall dass ![]() konstant ist, dass die Geschwindigkeit konstant ist
(Trägheitsgesetz)
konstant ist, dass die Geschwindigkeit konstant ist
(Trägheitsgesetz)
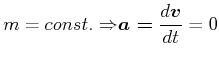 |
(4.213) |
Wenn die Kraft null ist, also
![]() oder
oder
![]() und gleichzeitig noch
und gleichzeitig noch
![]() ist, wird dieses System Inertialsystem genannt. Diese Konsequenz aus dem Grundgesetz der
Dynamik wird oft auch 1. Newtonsches Gesetz genannt.
ist, wird dieses System Inertialsystem genannt. Diese Konsequenz aus dem Grundgesetz der
Dynamik wird oft auch 1. Newtonsches Gesetz genannt.
Für einfache Probleme sind Differentialgleichungen gut. Bei komplizierteren Problemen und bei numerischen Verfahren sind Integrale aber viel geeigneter.
Frage: ein Ball fällt auf den Boden
![\includegraphics[height=0.13\textheight]{mechanik-021}](img852.gif)
![\includegraphics[height=0.13\textheight]{mechanik-022}](img853.gif)
Fallender Ball springt vom Boden hoch.
|
aus
![]()
folgt
![]()
und
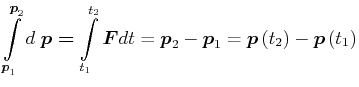 |
(4.214) |
Die Grösse
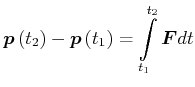 |
(4.215) |
heisst Kraftstoss. Der Kraftstoss kann zur Beschreibung rascher Vorgänge dienen.
Beispiel: ein Ball trifft mit der Geschwindigkeit ![]() auf dem Boden auf. Er berührt den Boden während
der Aufschlagzeit
auf dem Boden auf. Er berührt den Boden während
der Aufschlagzeit ![]() .
.
![\includegraphics[width=0.5\textwidth]{mechanik-023}](img860.gif)
|
Wir nehmen an, dass während dem Aufschlag die Kraft sich wie
![]() verhält.
Aus
verhält.
Aus ![]() kann man die halbe Kontaktzeit
kann man die halbe Kontaktzeit ![]() bestimmen
bestimmen
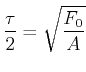 |
(4.216) |
Also ist
Wir erhalten
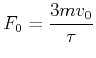 |
(4.218) |
das heisst, die Kraft wird desto grösser, je kürzer die Kontaktzeit ist. Eine Anwendung ist die Knautschzone bei Autos: je länger die Kontaktzeit ist, das heisst, je mehr die Kühlerhaube deformiert werden kann, desto kleiner sind die Kräfte auf die Insassen.
Beobachtung: jegliche Bewegung kommt zum Stillstand.
![\includegraphics[width=0.4\textwidth]{mechanik-024}](img872.gif)
Reibung
|
|
|
Die Gewichtskraft auf den Klotz ist
![]() .
.
Die Kraft zum Starten der Bewegung ist
| (4.219) |
Dabei ist ![]() die Haftreibungskraft und
die Haftreibungskraft und ![]() der Haftreibungskoeffizient.
der Haftreibungskoeffizient.
Um ![]() in gleichförmiger Bewegung zu halten brauchen wir die Kraft
in gleichförmiger Bewegung zu halten brauchen wir die Kraft
| (4.220) |
Hier is ![]() der Gleitreibungskoeffizient und
der Gleitreibungskoeffizient und ![]() die Gleitreibungskraft. Es gilt
die Gleitreibungskraft. Es gilt
| (4.221) |
![\includegraphics[width=0.45\textwidth]{mechanik-025}](img881.gif)
![\includegraphics[width=0.35\textwidth]{mechanik-026}](img882.gif)
Links: Reibungsmodell nach Amontons. Rechts ein moderneres Bild.
|
Woher rührt diese Gleitreibung? Guillaume Amontons (1663-1705) postulierte zwei Ursachen:
Modernere Bilder beschreiben die Reibung als ein Abscheren von gestauchten Mikrokontakten. Damit können zwei Phänomene erklärt werden:
Die wahre Kontaktfläche ist immer kleiner als die scheinbare. Durch Polieren erhöht man die wahre Kontaktfläche. Erhöht man die Auflagekraft, werden die mikroskopischen Kontakte mehr zusammengedrückt. Ihre wahre Kontaktfläche ist proportional zur Auflagekraft.
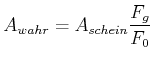 |
(4.222) |
wobei ![]() eine in diesem Model nicht weiter erklärte Konstante ist.
eine in diesem Model nicht weiter erklärte Konstante ist.
Die Reibungskraft hängt dann mit der Scherspannung, die notwendig ist zum Lösen des Kontakts mit der Unterlage,
![]() wie folgt zusammen
wie folgt zusammen
| (4.223) | ||
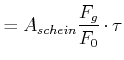 |
||
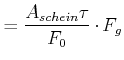 |
||
mit
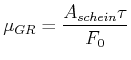 |
(4.224) |
Aus der Proportionalität der wahren Kontaktfläche mit der Auflagekraft und dem Modell der Scherung folgt das Reibungsgesetz der Gleitreibung mit einem konstanten, geschwindigkeitsunabhängigen (nach Coulomb) Reibungskoeffizienten.
Die Rollreibung entsteht durch die Deformation des Rollkörpers, zum Beispiel der Räder.
Aus Beobachtungen hat man das empirische Gesetz für die Strömungsgeschwindigkeit abgeleitet.
| (4.225) |
![]() und
und ![]() sind Konstanten,
sind Konstanten, ![]() hängt von der Form des bewegten Körpers ab (Widerstandsbeiwert). Die Einheit von
hängt von der Form des bewegten Körpers ab (Widerstandsbeiwert). Die Einheit von
![]() ist
ist
![]() . Das Bewegungsgesetz für einen frei fallenden Körper mit
konstanter Masse lautet (die Gravitationskraft gibt es ja auch!)
. Das Bewegungsgesetz für einen frei fallenden Körper mit
konstanter Masse lautet (die Gravitationskraft gibt es ja auch!)
| (4.226) |
Die Endgeschwindigkeit ![]() wird erreicht, wenn
wird erreicht, wenn ![]() ist, also
ist, also
| (4.227) |
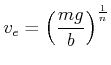 |
(4.228) |
Meist ist ![]() .
.
Ein Mensch (![]() ) im freien Fall hat etwa die Endgeschwindigkeit
) im freien Fall hat etwa die Endgeschwindigkeit
![]() . Sein Luftwiderstandsbeiwert
(Exponent
. Sein Luftwiderstandsbeiwert
(Exponent ![]() ) ist also
) ist also
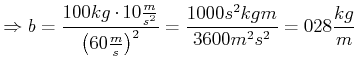
Wie gross muss der Luftwiderstandsbeiwert eines Fallschirms sein, damit der Mensch überlebt?
Wir betrachten ein linear beschleunigtes Bezugssystem.
![\includegraphics[width=0.5\textwidth]{mechanik-027}](img904.gif)
Linear beschleunigtes Bezugssystem
|
Durch die Beschleunigung zeigt die resultierende Kraft (Schwerkraft und Trägheitskraft) schräg nach unten. Dies kann mit einem Glas Wasser (halbvoll) beobachtet werden.
Wir betrachten ein rotierendes Bezugssystem.
![\includegraphics[width=0.7\textwidth]{mechanik-028}](img905.gif)
Rotierendes Bezugssystem
|
![]() ist die Corioliskraft.
ist die Corioliskraft.
Ein mitrotierender Beobachter wird die Coriolis-Kraft beobachten.
Beispiele für die Corioliskraft sind Hoch-und Tiefdruckgebiete.
Die Badewannenwirbel werden durch ein Aufschaukeln von Störungen, aber nicht durch die Corioliskraft erzeugt.
Othmar Marti