
Weiter: Strömungen Oben: Mechanik deformierbarer Medien Zurück: Flüssigkeiten und Gase Skript: PDF-Datei Übungen: Blätter ILIAS: Materialien Korrekturen
![\includegraphics[width=0.6\textwidth]{deform-016}](img2766.gif)
Molekulares Bild der Flüssigkeit. Links das Innere, rechts die Oberfläche. Obere Zeile: Kohäsionskräfte
an der Oberfläche sind nicht gleichverteilt. Untere Zeile: Stösse mit der Oberfläche erzeugen eine nach aussen
gerichtete Kraft.
|
Im Inneren einer Flüssigkeit (oder eines Gases) sind die anziehenden Kräfte (auch Kohäsionskräfte genannt) isotrop verteilt. Es gibt auf ein bestimmtes Atom keine Nettokraft. Kohäsionskräfte sind kurzreichweitig. Mehr als über zwei bis vier Atome oder Moleküle reichen sie nicht. Ebenso sind im Inneren der Flüssigkeit oder des Gases die Stösse und die Impulse isotrop verteilt. Die Stösse ergeben also im Mittel keine Kraft. Dabei ist die Standardabweichung nicht null: dies führt zur Brownschen Bewegung.
An der Oberfläche einer Flüssigkeit existieren mindestens zwei, im Gravitationsfeld drei Kräfte.
Da die Oberfläche in Ruhe ist, müssen die drei Kräfte im Gleichgewicht sein. Die aus dem Impulsübertrag resultierende Kraft nach aussen muss also gleich der Kohäsionskraft und, eventuell, der Gravitation oder anderer äusserer Kräfte, sein.
Da die Oberfläche stabil ist, bedeutet dies auch, dass die potentielle Energie eines Atoms oder Moleküls im
Inneren tiefer liegen muss als ausserhalb der Flüssigkeit. Dies kann auch so verstanden werden, dass für jedes
Teilchen im Inneren im Mittel ![]() Kohäsionspotentiale (alle
Kohäsionspotentiale (alle ![]() !)aufsummiert werden müssen, während an der
Oberfläche nur
!)aufsummiert werden müssen, während an der
Oberfläche nur ![]() Potentiale zum Summieren vorhanden sind. Die Summe aller Kohäsionspotentiale an der
Oberfläche ist also weniger negativ als im Inneren. Der Energieunterschied pro Fläche ist dann die
Oberflächenenergie.
Potentiale zum Summieren vorhanden sind. Die Summe aller Kohäsionspotentiale an der
Oberfläche ist also weniger negativ als im Inneren. Der Energieunterschied pro Fläche ist dann die
Oberflächenenergie.
Diese Oberflächenenergie kann berechnet werden, wenn man annimmt, dass die Stösse mit der Oberfläche
unveränderlich eine konstante nach aussen gerichtete Kraft erzeugen. Schiebt sich nun ein Molekül ![]() an die
Oberfläche, so leistet es die Arbeit
an die
Oberfläche, so leistet es die Arbeit
![]() gegen
gegen
![]() . Damit wird
. Damit wird
Der Index ![]() bezeichnet dabei die Oberfläche (surface). Die gesamte Energie der Oberfläche wird berechnet, indem
aufsummiert (oder integriert) wird.
bezeichnet dabei die Oberfläche (surface). Die gesamte Energie der Oberfläche wird berechnet, indem
aufsummiert (oder integriert) wird.
Die potentielle Energie der gesamten Oberfläche ![]() (eventuell berandet) ist minimal, wenn die Oberfläche minimal
ist. Die Gesamtenergie
(eventuell berandet) ist minimal, wenn die Oberfläche minimal
ist. Die Gesamtenergie ![]() hängt mit der Oberfläche
hängt mit der Oberfläche ![]() und der Oberflächenspannung
und der Oberflächenspannung ![]() wie
folgt zusammen:
wie
folgt zusammen:
| (7.698) |
Die Einheit der Oberflächenspannung
![]() ist
ist
![]() .
.
Wenn ![]() Moleküle an der Oberfläche sind, gilt
Moleküle an der Oberfläche sind, gilt
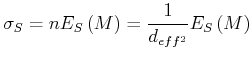 |
(7.699) |
Dabei ist
![]() die Flächendichte der Moleküle,
die Flächendichte der Moleküle, ![]() der effektive Durchmesser eines
Moleküls und
der effektive Durchmesser eines
Moleküls und
![]() die Arbeit, die benötigt wird um ein Molekül gegen die
Oberflächenkraft an die Oberfläche zu bringen (siehe Gleichung (7.62) ).
die Arbeit, die benötigt wird um ein Molekül gegen die
Oberflächenkraft an die Oberfläche zu bringen (siehe Gleichung (7.62) ).
![\includegraphics[width=0.5\textwidth]{deform-017}](img2782.gif)
|
| (7.700) |
| (7.701) |
Pro Flüssigkeitsoberfläche wirkt auf die Breite ![]() die Kraft.
die Kraft.
| (7.702) |
![\includegraphics[width=0.13\textwidth]{deform-018}](img2787.gif)
Tropfenzähler
|
Der Querschnitt ist ![]() . Das Kräftegleichgewicht verlangt, dass die
aufwärtsgerichte Kraft der Oberflächenspannung gerade das Gewicht des Tropfens kompensiert. Ausser an der
Berandung kompensieren sich alle Kräfte.
. Das Kräftegleichgewicht verlangt, dass die
aufwärtsgerichte Kraft der Oberflächenspannung gerade das Gewicht des Tropfens kompensiert. Ausser an der
Berandung kompensieren sich alle Kräfte.
| (7.703) |
Also ist
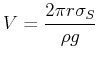 |
(7.704) |
Also kann man mit der obigen Physik einen Tropfenzähler beschreiben.
![\includegraphics[width=0.4 \textwidth]{deform-019}](img2791.gif)
Krümmungsradien bei einer freien Oberfläche
|
Die Oberfläche ist charakterisiert durch 2 Krümmungsradien ![]() und
und ![]()
Behauptung
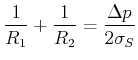 |
(7.705) |
Beweis für eine Kugel
![\includegraphics[width=0.3\textwidth]{deform-020}](img2795.gif)
Oberflächenspannung und Druck in einer Kugel
|
Wir haben eine Äquatorialfläche ![]() und einen Äquatorialumfang
und einen Äquatorialumfang ![]() . Die Druckkraft ist
. Die Druckkraft ist
![]() , die
Oberflächenspannung am Umfang
, die
Oberflächenspannung am Umfang
![]() (da wir 2 Oberflächen haben!)
(da wir 2 Oberflächen haben!)
Also
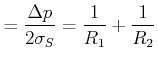 |
(7.706) |
da bei der Kugel
![]() ist.
ist.
Beispiel:
Seifenblasen.
Die kleinere Seifenblase hat den grösseren Druck (gilt auch für Luftballons, wieso?)
Freie nicht geschlossene Oberflächen sind Minimalflächen mit
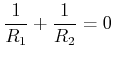 |
(7.707) |
Da der Krümmungsradius
![]() ist, gilt auch
ist, gilt auch
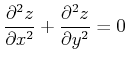 |
(7.708) |
![\includegraphics[width=0.5\textwidth]{deform-021}](img2808.gif)
Benetzende Flüssigkeiten
|
Steigt die Flüssigkeit um ![]() wird das Volumen
wird das Volumen
![]() über den Spiegel der
Flüssigkeit ausserhalb der Kapillare gehoben. Die Gewichtskraft dieses Volumens
über den Spiegel der
Flüssigkeit ausserhalb der Kapillare gehoben. Die Gewichtskraft dieses Volumens ![]() muss von der
Oberflächenspannung entlang des Umfangs
muss von der
Oberflächenspannung entlang des Umfangs ![]() getragen werden.
getragen werden.
| (7.709) |
| (7.710) |
und
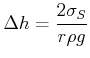 |
(7.711) |
Bei Nichtbenetzung beobachtet man eine Kapilardepression (Beispiel Glas und Quecksilber).
Wann immer zwei beliebige Substanzen sich berühren, existieren Grenzflächenenergien.
![\includegraphics[width=0.5\textwidth]{deform-022}](img2814.gif)
|
Für benetzende Flüssigkeiten ist
![]() negativ. Da die Randlinie sich nicht bewegt, muss
negativ. Da die Randlinie sich nicht bewegt, muss
| (7.712) |
| (7.713) |
Wenn
![]() ist, müsste
ist, müsste
![]() sein. Es gibt deshalb einen
reellen Winkel
sein. Es gibt deshalb einen
reellen Winkel ![]() und kein Kräftegleichgewicht. Die Flüssigkeit kriecht deshalb die Wand hoch.
und kein Kräftegleichgewicht. Die Flüssigkeit kriecht deshalb die Wand hoch.
Wenn
![]() ist, das heisst, wenn
ist, das heisst, wenn
![]() ist, steigt der
Flüssigkeitsspiegel am Rande nicht an, sondern wird nach unten gedrückt. Der Randwinkel
ist, steigt der
Flüssigkeitsspiegel am Rande nicht an, sondern wird nach unten gedrückt. Der Randwinkel ![]() ist dann
ist dann
![]() . Quecksilber in einem Glasgefäss zeigt dieses Verhalten.
. Quecksilber in einem Glasgefäss zeigt dieses Verhalten.
An der Grenze wo Luft, Flüssigkeit und die feste Wand sich berühren müssen die Adhäsions- und Kohäsionskräfte im Gleichgewicht sein. Die Adhäsionskräfte beschreiben die Kräfte zwischen der Flüssigkeit und der festen Wand. Die Adhäsionskräfte zwischen dem Dampf und der Wand werden vernachlässigt. Die Flüssigkeit selber wird durch Kohäsionskräfte, die anziehenden Kräfte zwischen den Molekülen, zusammengehalten.
Für ein Molekül an der Grenzlinie gibt es die Adhäsionskraft zur Wand. Diese Kraft
![]() steht senkrecht
zur Wand. Die Kohäsionskräfte werden durch die anderen Flüssigkeitsmoleküle aufgebracht. Die resultierende
Kohäsionskraft
steht senkrecht
zur Wand. Die Kohäsionskräfte werden durch die anderen Flüssigkeitsmoleküle aufgebracht. Die resultierende
Kohäsionskraft
![]() muss entlang der Winkelhalbierenden zwischen der Tangente zur Oberfläche und zur
Wand liegen. Da die Oberfläche keine Scherkraft aufnehmen kann, muss die resultierende Kraft senkrecht zur
Flüssigkeitsoberfläche liegen. Wir beobachten
muss entlang der Winkelhalbierenden zwischen der Tangente zur Oberfläche und zur
Wand liegen. Da die Oberfläche keine Scherkraft aufnehmen kann, muss die resultierende Kraft senkrecht zur
Flüssigkeitsoberfläche liegen. Wir beobachten
![\includegraphics[width=0.7\textwidth]{deform-023}](img2827.gif)
Kohäsion und Adhäsion bei Benetzung und ohne Benetzung
|
Der Grenzwinkel ![]() zwischen der Flüssigkeit und der Wand (in der Flüssigkeit!) kann mit dem folgenden Ansatz
ausgerechnet werden. Wir legen die
zwischen der Flüssigkeit und der Wand (in der Flüssigkeit!) kann mit dem folgenden Ansatz
ausgerechnet werden. Wir legen die ![]() -Achse horizontal nach rechts, die
-Achse horizontal nach rechts, die ![]() -Achse nach oben. Die auf ein Teilchen
an der Grenzlinie im Winkel
-Achse nach oben. Die auf ein Teilchen
an der Grenzlinie im Winkel ![]() wirkende Kohäsionskraft kann mit der Kohäsionskraft im Inneren (in einer
Ebene) als
wirkende Kohäsionskraft kann mit der Kohäsionskraft im Inneren (in einer
Ebene) als
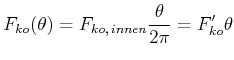
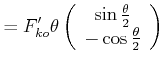 |
||
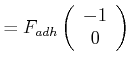 |
||
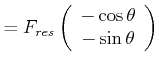 |
Wir können mit dem Kräftegleichgewicht, das heisst der resultierenden Kraft 0, für die ![]() -und
-und ![]() -Richtung zwei
Gleichungen aufstellen
-Richtung zwei
Gleichungen aufstellen
| (7.714) |
Eingesetzt haben wir
Aus der zweiten Gleichung in Gleichung (7.80) bekommen wir mit
![]()
Wir multiplizieren das Resultat aus Gleichung (7.81) mit
![]() in die erste Gleichung aus
Gleichung (7.80) ein und erhalten
in die erste Gleichung aus
Gleichung (7.80) ein und erhalten
Dies ist ein bemerkenswertes Resultat: Der Betrag der resultierenden Kraft hängt nur von der Adhäsionskraft ab, nicht aber von der Kohäsionskraft.
Wir setzen das Resultat aus Gleichung (7.82) zurück in die Gleichung (7.81) ein und erhalten die transzendente Gleichung
Wenn wir annehmen, dass
![]() ist mit
ist mit
![]() , so erhalten wir
, so erhalten wir
Diese Gleichung gilt nur da wo
![]() ist
ist
Othmar Marti