
Weiter: Beschleunigung Oben: Geschwindigkeiten und Beschleunigungen in Zurück: Geschwindigkeiten und Beschleunigungen in Skript: PDF-Datei Übungen: Blätter ILIAS: Materialien Korrekturen
Wir wissen, dass in kartesischen Koordinaten
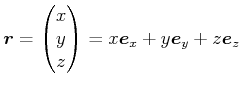 |
(G..957) |
der Ortsvektor ist. Die Geschwindigkeit ist dann
Wir verwenden die Beziehungen
| (G..959) | ||
| (G..960) | ||
| (G..961) |
und leiten sie ab. Wir erhalten
Wir setzen in die Gleichung G.12 die Gleichungen G.8, G.9,
G.10, G.16, G.17 und G.18 ein und ordnen nach
![]() ,
,
![]() und
und
![]() .
.
| (G..965) | ||
Der Übersichtlichkeit halber berechnen wir nun die drei Komponenten
![]() ,
,
![]() und
und
![]() getrennt. Wir beginnen
mit
getrennt. Wir beginnen
mit
![]() .
.
| (G..966) | ||
![$\displaystyle \left[ \dot{r}\sin(\theta)\cos(\phi)+r\cos(\theta)\cos(\phi)\dot{\theta }-r\sin(\theta)\sin(\phi)\dot{\phi}\right] \sin(\theta)\cos(\phi)$](img3910.gif) |
||
![$\displaystyle +\left[ \dot{r}\sin(\theta)\sin(\phi)+r\cos(\theta)\sin(\phi)\dot{\theta }+r\sin(\theta)\cos(\phi)\dot{\phi}\right] \sin(\theta)\sin(\phi)$](img3911.gif) |
||
![$\displaystyle +\left[ \dot{r}\cos(\theta)-r\sin(\theta)\dot{\theta}\right] \cos (\theta)$](img3912.gif) |
||
Wir fahren mit
![]() weiter.
weiter.
| (G..967) | ||
![$\displaystyle \left[ \dot{r}\sin(\theta)\cos(\phi)+r\cos(\theta)\cos(\phi)\dot{\theta }-r\sin(\theta)\sin(\phi)\dot{\phi}\right] \cos(\theta)\cos(\phi)$](img3925.gif) |
||
![$\displaystyle +\left[ \dot{r}\sin(\theta)\sin(\phi)+r\cos(\theta)\sin(\phi)\dot{\theta }+r\sin(\theta)\cos(\phi)\dot{\phi}\right] \cos(\theta)\sin(\phi)$](img3926.gif) |
||
![$\displaystyle -\left[ \dot{r}\cos(\theta)-r\sin(\theta)\dot{\theta}\right] \sin (\theta)$](img3927.gif) |
||
Wir schliessen mit
![]() .
.
| (G..968) | ||
![$\displaystyle -\left[ \dot{r}\sin(\theta)\cos(\phi)+r\cos(\theta)\cos(\phi)\dot{\theta }-r\sin(\theta)\sin(\phi)\dot{\phi}\right] \sin(\phi)$](img3939.gif) |
||
![$\displaystyle +\left[ \dot{r}\sin(\theta)\sin(\phi)+r\cos(\theta)\sin(\phi)\dot{\theta }+r\sin(\theta)\cos(\phi)\dot{\phi}\right] \cos(\phi)$](img3940.gif) |
||
Zusammenfassend haben wir
| (G..969) | ||
Othmar Marti