2.1  Maxwellgleichungen

(Siehe Leisi, Klassische Physik II [Lei98, pp. 251])

Alle optischen Phänomene können mit den Maxwellgleichungen berechnet werden.

Hier ist 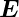das elektrische Feld, 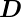die dielektrische Verschiebung, 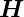das magnetische Feld, 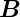die magnetische Induktion, 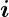die mikroskopische Stromdichte und ρ_el die Ladungsdichte.

Weiter benötigen wir das Kraftgesetz

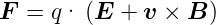(2.2)

und die Kontinuitätsgleichung

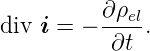(2.3)

Die angegebenen Maxwellgleichungen gelten für alle Medien, auch mit tensoriellen Eigenschaften. Dort benötigt man die beiden Materialgleichungen

um das elektrische Feld und die dielektrische Verschiebung, bzw. das magnetische Feld und die magnetische Induktion miteinander zu verknüpfen, wobei 𝜀 (relative Permittivität) und μ (relative Permeabilität) Tensoren sein können. 𝜀₀ ist die Permittivität des Vakuums, μ₀ die Permeabilität des Vakuums.

Die Integralformulierung der Maxwellgleichungen lauten

Die Integralformulierung des Kontinuitätsgesetzes lautet

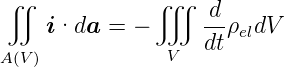(2.6)