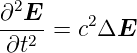
Aus den Maxwellgleichungen folgen Wellengleichungen. Für das Vakuum erhält man
|
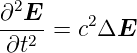| (2.1) |
oder
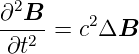 | (2.2) |
In jedem Inertialsystem im Vakuum ist die Ausbreitungsgeschwindigkeit
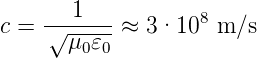 | (2.3) |
In Medien ist die Ausbreitungsgeschwindigkeit entsprechend
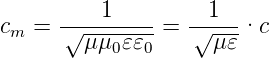 | (2.4) |
wobei μ die relative Permeabilität und 𝜀 die relative Permittivität ist.
Alle Funktionen (skalar, vektoriell oder tensoriell), die nur von einer skalaren Variablen
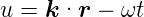 | (2.5) |
abhängen lösen die Wellengleichung, wenn sie genügend oft stetig differenzierbar sind.
Damit können wir sagen: Jede Funktion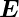 
(u) mit
u = 
·
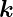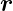−ωt ist eine Lösung der Wellengleichung
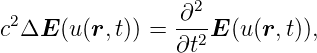 | (2.6) |
sofern
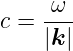 | (2.7) |
gilt.
Aus den Gleichungen Maxwellgleichungen kann die
Orientierung von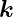 
, 
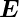und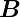 
berechnet werden.
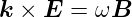 | (2.8) |
, 
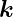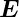und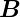 
bilden in dieser Reihenfolge ein rechtshändiges
Dreibein. Die drei Vektoren stehen paarweise rechtwinklig
aufeinander.
Aus der Wellengleichung für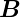 
, bekommen wir die
Beziehung
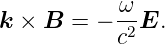 | (2.9) |
Diese Beziehung (2.9) ist aber unter Verwendung von (2.7) identisch mit (2.8).
Betragsmässig haben wir im Vakuum weiter die Beziehung
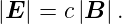 | (2.10) |
Lizenzinformationen