
| Literatur | |
Zur Behandlung von Resonatoren verwenden wir die Matrixdarstellung der Lichtausbreitung paraxialer Strahlen in einer zylindersymmetrischen Anordnung. Die Lage des Lichtstrahls wird durch den Vektor
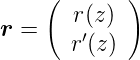 | (7.1) |
wobei z die Koordinate entlang der optischen Achse ist. Die Wirkung eines optischen Elementes wird durch eine Matrix A beschrieben
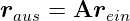 | (7.2) |
Für eine Gerade haben wir die Geradengleichung
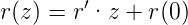 | (7.3) |
Wir kennen r(z0) und r′(z0) sowie z1 = z0 + d und haben dann
__________________________________________________________________________
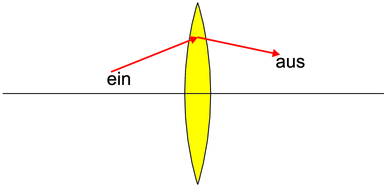
Skizze zur Berechnung der Linsenmatrix
_____________________________________________________________________
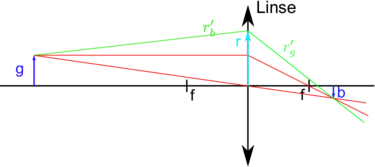
In Abbildung 7.1.2 ist der Strahlengang von einem Gegenstand mit der Gegenstandshöhe G im Abstand g von der Linse zu einem Bild mit der Bildhöhe B < 0 im Abstand b zur Linse aufgezeichnet. Wir interessieren uns für den grünen Strahl mit der ursprünglichen Steigung rg′. Gesucht ist die Steigung rb′ an der Linse im Abstand r = rg = rb.
Wir können die folgenden Gleichungen aufstellen:
__________________________________________________________________________
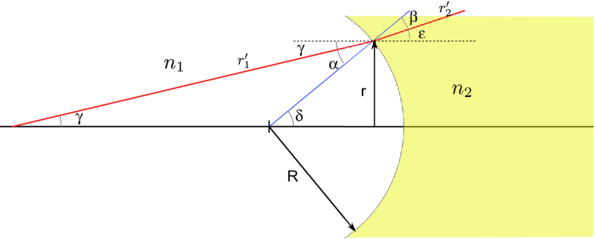
Skizze zur Berechnung der Matrix für eine gewölbte Grenzfläche
_____________________________________________________________________
In Abbildung 7.1.3 betrachten wir zuerst Winkelbeziehungen
und die weiteren Beziehungen
und damit
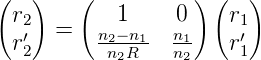 | (7.8) |
und mit R →∞ auch für eine ebene Grenzfläche senkrecht zur optischen Achse
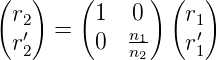 | (7.9) |
__________________________________________________________________________
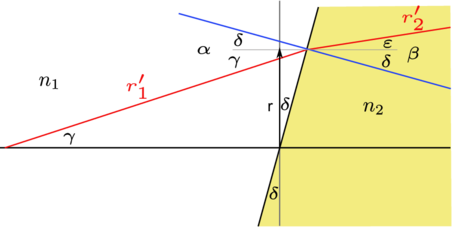
Skizze zur Berechnung der Matrix für eine schräge Grenzfläche
_____________________________________________________________________
Wir betrachten in Abbildung 7.1.4 eine Grenzfläche zwischen Medien mit n1 und n2, die um den Winkel δ gegen die Normale auf die optische Achse geneigt ist.
Wir haben die folgenden Beziehungen:
Diesmal gibt es zur Matrixgleichung noch einen konstanten Term
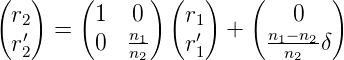 | (7.11) |
Für δ = 0 erhalten wir das Resultat für eine Grenzfläche senkrecht zur optischen Achse.
__________________________________________________________________________
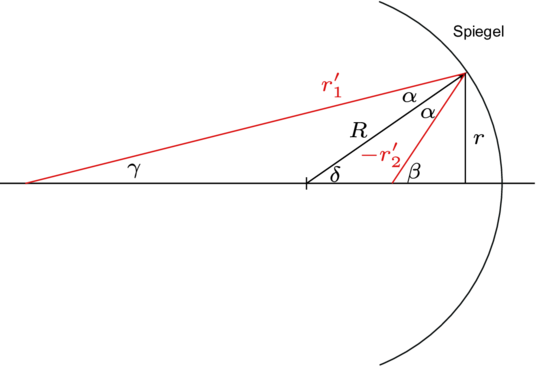
Skizze zur Berechnung der Matrix für einen Spiegel.
_____________________________________________________________________
Nach der Abbildung 7.1.5 gelten die folgenden Winkelbeziehungen:
Mit den Beziehungen r1′ = tan(γ) ≈γ und −r2′ = tan(β) ≈β erhalten wir
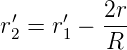 | (7.13) |
und
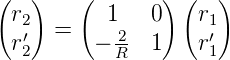 | (7.14) |
Wir betrachten hier nach Yariv [Yar75, pp. 106] ein sogenanntes quadratiesches Indexmedium, also ein Medium, das die folgende Variation des Brechungsindexes hat
![[ ]
-k2 2 2
n(x,y ) = n0 1 − 2k (x + y )](op-2016-2017834x.png) | (7.15) |
Mit dem Fermatschen Prinzip in differentieller Schreibweise
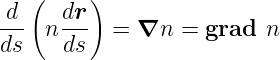 | (7.16) |
kann die Trajektorie des Lichtstrahls ausgerechnet werden. Dabei ist s die Weglänge entlang des Lichtstrahls. Bei paraxialen Strahlen kann d∕ds durch d∕dz ersetzt werden.
![( ) [ ]
-d- n dr- = n grad 1 − k2(x2 + y2) = − n0k2-r
dz dz 0 2k k](op-2016-2017836x.png) | (7.17) |
Da n nicht von z abhängt, ist auch
![d ( dr ) d2r n k [ k ] d2r
--- n--- = n --2-= − --0-2r = n0 1 − -2-(x2 + y2) ---2
dz dz dz k 2k dz](op-2016-2017837x.png) | (7.18) |
Nehmen wir nun weiter an, dass 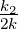 (x2 + y2) « 1 ist, so
können wir schreiben:
(x2 + y2) « 1 ist, so
können wir schreiben:
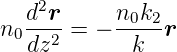 | (7.19) |
Uns interessiert nur der Abstand r = 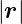 . Da n0 > 0
ist, kann es eliminiert werden. Damit erhalten wir die
Differentialgleichung für paraxiale Strahlen
. Da n0 > 0
ist, kann es eliminiert werden. Damit erhalten wir die
Differentialgleichung für paraxiale Strahlen
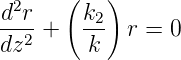 | (7.20) |
Wenn der Strahl am Eingang die Position r0 und die Steigung r0′ hat, ist die Lösung
Wir haben also für ein quadratisches Indexmedium mit k2 > 0 der Länge ℓ
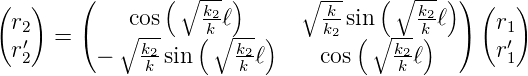 | (7.22) |
Wenn k2 < 0 ist, wenn wir also eine Zerstreuungslinse haben, bekommen wir
Wir haben also für ein quadratisches Indexmedium mit k2 < 0 der Länge ℓ
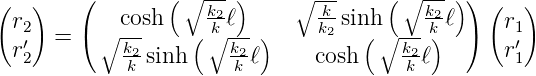 | (7.24) |
___________________________________________________________________________
| GeradeStrecke | 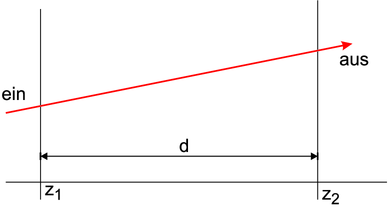 | 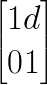 |
 | 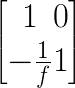 |
|
| Dielektrische
Grenzschicht
mit den
Brechungsindizes
n1 und n2 | 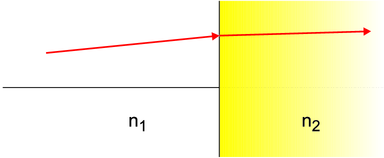 | 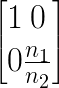 |
| Sphärische
dielektrische
Grenzschicht
mit
Krümmungsradius
R und den
Brechungsindizes
n1 und n2 | 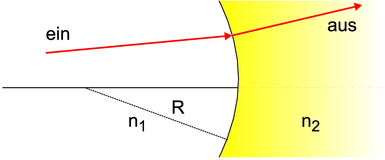 | 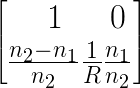 |
| Sphärischer
Spiegel
mit dem
Krümmungsradius
R | 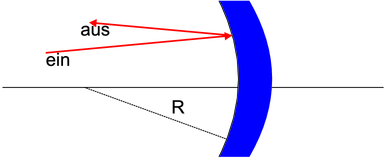 | 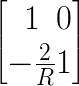 |
| GeradeStrecke | 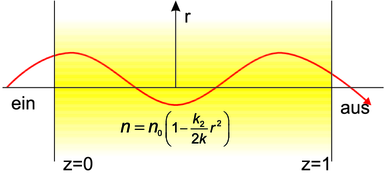 | 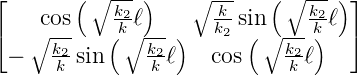 |
_____________________________________________________________________
_____________________________________________________________________
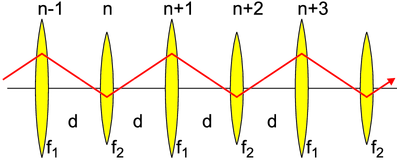
Linsenübertragungsstrecke als Modell für einen Laserresonator.
_____________________________________________________________________
Der Strahl von der n-ten zur n + 1-ten Linse ist durch
![[ ] [ ] [ ]
1 0 1 d 1 d
raus = − 1f 1 0 1 rein = − 1f − fd+ 1 rein](op-2016-2017852x.png) | (7.25) |
Wir haben dann eine Lichtausbreitung in einem Resonator, wenn die Strahllage nach der n + 2-ten Linse gleich wie nach der n-ten ist. Daraus folgt
![[ ] [ ]
r = 1 d 1 d r
aus − 1f1 − fd1 + 1 − 1f2- − fd2 + 1 ein](op-2016-2017853x.png) | (7.26) |
Ausmultipliziert erhalten wir
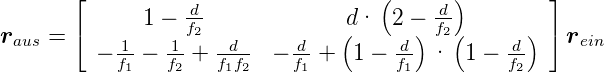 | (7.27) |
Um eine Resonatormode zu bekommen muss 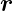 aus =
aus = 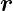 ein
sein. Wir setzen
ein
sein. Wir setzen
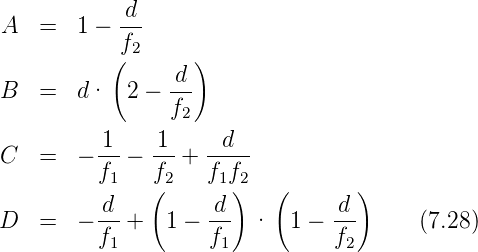
Damit bekommen wir auch
Wir lösen die erste Gleichung nach rn′ auf und erhalten
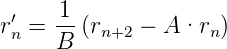 | (7.30) |
Diese Gleichung schreiben wir um 2 verschoben hin und bekommen
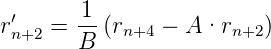 | (7.31) |
Wir setzen diese Resultate in die zweite Gleichung (7.29) ein und erhalten
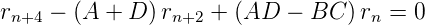 | (7.32) |
Durch ausrechnen erhält man, dass AD −BC = 1 ist.
Wenn wir b = 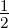
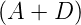 =
= 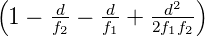 setzen,
können wir schreiben
setzen,
können wir schreiben
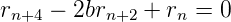 | (7.33) |
Diese Differenzengleichung ist formal
äquivalent zu einer Differentialgleichung vom Typ
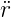 +kr = 01
Die Lösung der Differentialgleichung ist r(z) = r(0) exp
+kr = 01
Die Lösung der Differentialgleichung ist r(z) = r(0) exp ![[ √ --]
±i kz](op-2016-2017867x.png) .
Deshalb setzen wir in die Differenzengleichung den Ansatz
rs = r0 exp
.
Deshalb setzen wir in die Differenzengleichung den Ansatz
rs = r0 exp ![[isΘ ]](op-2016-2017868x.png) mit s = 2n ein und erhalten
mit s = 2n ein und erhalten
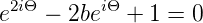 | (7.34) |
Die Lösung ist
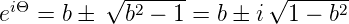 | (7.35) |
Mit b = cos Θ und daraus 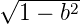 = sin Θ ist die obige
Gleichung erfüllt. Die allgemeine Lösung ist also
= sin Θ ist die obige
Gleichung erfüllt. Die allgemeine Lösung ist also
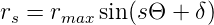 | (7.36) |
mit rmax = r0∕ sin δ. Damit wir eine stabile Lösung haben, muss Θ reell sein. Daraus folgt
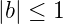 | (7.37) |
Aus der Definition von b folgt2
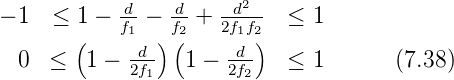
Wenn wir die neuen normierten Koordinaten g1 = 1 −d∕(2f1) und g2 = 1 −d∕(2f2) einführen, heisst die Stabilitätsbedingung
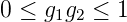 | (7.39) |
__________________________________________________________________________
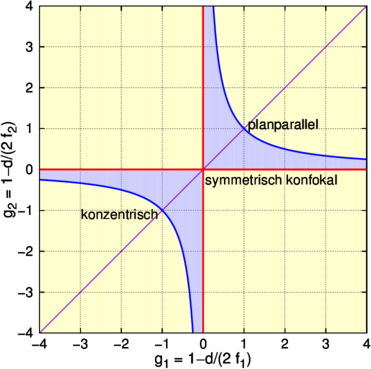
Stabilitätsdiagramm für Strahlführoptiken mit Linsen. Die gelbliche Farbe zeigt die instabilen Bereich, die türkis-Farbe die stabilen.
_____________________________________________________________________
Das obige Stabilitätsdiagramm kann auch für Spiegel berechnet werden, indem man f = R∕2 setzt, wobei R der Krümmungsradius des Spiegels ist.
__________________________________________________________________________
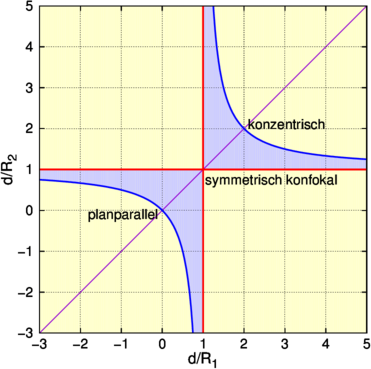
Das Stabilitätsdiagramm für Spiegelresonatoren.
_____________________________________________________________________
| Versuch zur Vorlesung: | |
| Laser (Versuchskarte AT-052) | |
 Lizenzinformationen
Lizenzinformationen