©2002-2017 Ulm University, Othmar Marti, 
[Nächste
Seite] [Vorherige Seite] [vorheriges Seitenende] [Seitenende]
[Ebene nach oben] [PDF-Datei][Epub-Datei][Andere
Skripte]
2.3 Die Fresnelschen Formeln
(Siehe Hecht, Optik [Hec05, pp. 190]) (Siehe Gerthsen,
Physik [Mes06, pp. 539])
__________________________________________________________________________
Das gleiche Gebäude mit Polarisationsfilter
aufgenommen. Die Achse des Polarisationsfilters wurde
dabei um 90° gedreht. Links sind die Reflexionen im
Glas kaum zu erkennen, rechts ist dafür der Kontrast des
Himmels schwächer.
_____________________________________________________________________
Die beiden Aufnahmen in Abbildung 2.3 wurden mit dem
Polarisationsfilter in zwei um 90° gedrehten Stellungen
aufgenommen. Links wird durch den Polarisator das diffus
gestreute Licht mit der falschen Polarisation unterdrückt.
Links ist die Spiegelung des linken Gebäudes im rechten nicht
sichtbar, Die Fensterfront ist hell. Rechts ist das linke
Gebäude dunkel. Das bedeutet, dass das gespiegelte Licht
polarisiert ist. Die im folgenden abgeleiteten Fresnelschen
Formeln erklären dieses Phänomen, aber auch die Spiegelung
an Metallen. Sie beschreiben die Wechselwirkung von
elektromagnetischen Wellen mit Grenzflächen jeder Art.
__________________________________________________________________________
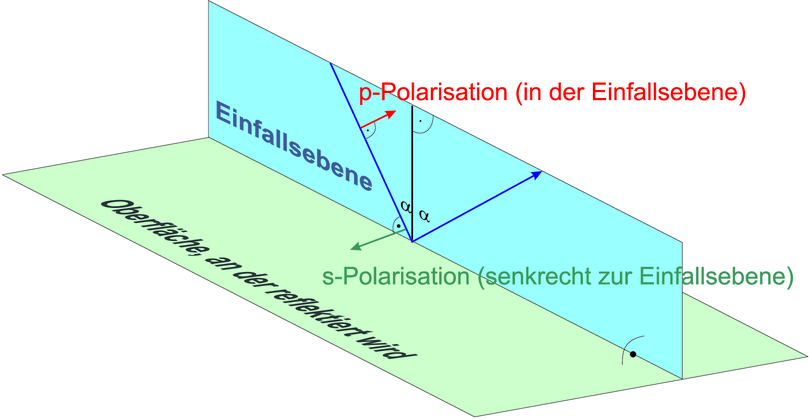
Definition der s-Polarisation und der p-Polarisation
_____________________________________________________________________
Die Reflexion und die Brechung von elektromagnetischen
Wellen werden durch die Maxwellschen Gleichungen und die
daraus abgeleiteten Randbedingungen bestimmt. Die
resultierenden Beziehungen für die Amplituden und die
Intensitäten werden die Fresnelschen Formeln genannt. Zur
Berechnung verwenden die Definitionen
- Der einfallende und
der reflektierte Strahl elektromagnetischer Wellen
definiert die Einfallsebene. Diese ist senkrecht zur
Grenzfläche der beiden Medien.
- Elektromagnetische Wellen, deren
Polarisationsebene senkrecht zur Einfallsebene liegt,
heissen s-polarisiert. Die Polarisationsebene gibt die
Richtung des elektrischen Feldes an.
- Elektromagnetische Wellen,
deren Polarisationsebene parallel zur Einfallsebene
liegt, heissen p-polarisiert.
- Für die Intensität der elektromagnetischen Wellen
in nichtmagnetischen Medien gilt I ∝
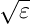 E2
, wobei
𝜀 = n2 ist.
E2
, wobei
𝜀 = n2 ist.
- Genauer gilt für die Intensität: I =
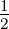
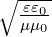 E2 =
E2 =
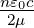 E2 für sinusförmige Wellen mit der Amplitude
E.
E2 für sinusförmige Wellen mit der Amplitude
E.
Wir betrachten eine Welle 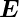 e, die aus dem Medium mit μ1
und 𝜀1 auf eine ebene Grenzfläche zum Medium mit μ2 und
𝜀2 fällt. Neben der einfallenden Welle existierten eine
reflektierte und eine transmittierte elektromagnetische
Welle
e, die aus dem Medium mit μ1
und 𝜀1 auf eine ebene Grenzfläche zum Medium mit μ2 und
𝜀2 fällt. Neben der einfallenden Welle existierten eine
reflektierte und eine transmittierte elektromagnetische
Welle
Gegeben sind 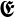 e, μ1, 𝜀1, μ2, 𝜀2,
e, μ1, 𝜀1, μ2, 𝜀2, 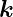 e und ωe
e und ωe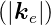 . An den
Grenzflächen gilt
. An den
Grenzflächen gilt
- Die tangentiale Komponente von
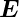 ist stetig.
ist stetig.
- Die tangentiale Komponente von
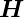 ist stetig.
ist stetig.
Sei 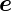 n der Normaleneinheitsvektor auf die Grenzfläche. Der
resultierende Vektor des Kreuzproduktes von
n der Normaleneinheitsvektor auf die Grenzfläche. Der
resultierende Vektor des Kreuzproduktes von 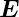 e mit
e mit 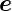 n liegt
senkrecht zu
n liegt
senkrecht zu 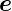 n und damit in der Grenzfläche der beiden
Medien. Um den Tangentialvektor in die ursprüngliche
Richtung zurück zu drehebn, wenden wir nochmals ein
Kreuzprodukt mit
n und damit in der Grenzfläche der beiden
Medien. Um den Tangentialvektor in die ursprüngliche
Richtung zurück zu drehebn, wenden wir nochmals ein
Kreuzprodukt mit 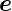 n an. Unabhängig von der Richtung
von
n an. Unabhängig von der Richtung
von 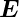 e bekommt man mit dieser Operation immer die
Komponente von
e bekommt man mit dieser Operation immer die
Komponente von 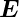 e tangential zur Grenzfläche
e tangential zur Grenzfläche
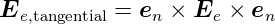 | (2.2) |
Mit der gleichen Methode kann man auch die Komponenten
der Vektoren 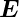 r und
r und 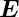 t in der Grenzfläche berechnen. Die
Bedingung der Stetigkeit der Tangentialkomponente des
elektrischen Feldes kann dann mit den Kreuzprodukten so
geschrieben werden
t in der Grenzfläche berechnen. Die
Bedingung der Stetigkeit der Tangentialkomponente des
elektrischen Feldes kann dann mit den Kreuzprodukten so
geschrieben werden
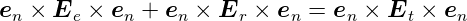 | (2.3) |
Die Gleichung besagt, dass die Summe der Tangentialkomponenten
des elektrischen Feldes im Medium 1 (einfallende und
reflektierte Welle) gleich der Tangentialkomponente der
transmittierten Welle ist. Für alle Zeiten und alle Orte auf der
Grenzfläche gilt
wobei 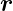 nach Definition ein Vektor in der Grenzfläche ist,
also mit
nach Definition ein Vektor in der Grenzfläche ist,
also mit 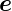 n·
n·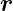 = 0. Damit Gleichung (2.4) zu allen Zeiten an
einem beliebigen Punkt gilt, müssen die Kreisfrequenzen
gleich sein
= 0. Damit Gleichung (2.4) zu allen Zeiten an
einem beliebigen Punkt gilt, müssen die Kreisfrequenzen
gleich sein
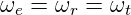 | (2.5) |
Weiter muss dann gelten: Die Gleichung (2.4) muss für alle
Zeiten und alle Orte auf der Grenzfläche gelten. Deshalb
gilt
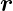 zeigt auf einen Punkt in der Grenzfläche. Da der Ursprung
des Koordinatensystems nicht in der Grenzfläche liegen muss,
ist
zeigt auf einen Punkt in der Grenzfläche. Da der Ursprung
des Koordinatensystems nicht in der Grenzfläche liegen muss,
ist 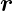 im Allgemeinen nicht parallel zur Grenzfläche. Aus der
ersten Gleichung in (2.6) folgt
im Allgemeinen nicht parallel zur Grenzfläche. Aus der
ersten Gleichung in (2.6) folgt
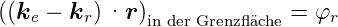 | (2.7) |
Eine Gleichung vom Typ 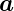 ·
·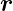 = ϖ beschreibt eine
Ebene. Die Endpunkte von
= ϖ beschreibt eine
Ebene. Die Endpunkte von 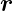 liegen in der Ebene mit dem
Normalenvektor
liegen in der Ebene mit dem
Normalenvektor 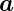 . ϖ gibt die Verschiebung zum Nullpunkt
an. Gleichung (2.7) ist also die Gleichung einer Ebene,
die senkrecht zu
. ϖ gibt die Verschiebung zum Nullpunkt
an. Gleichung (2.7) ist also die Gleichung einer Ebene,
die senkrecht zu 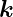 e −
e −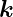 r liegt. Andererseits wissen wir,
nach unserer Konstruktion, dass
r liegt. Andererseits wissen wir,
nach unserer Konstruktion, dass 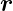 in der Grenzfläche
mit dem Normalenvektor
in der Grenzfläche
mit dem Normalenvektor 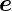 n liegt.
n liegt. 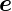 n ist also parallel zu
n ist also parallel zu
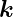 e −
e −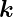 r. Weiter sind beide Wellen im gleichen Medium
1, das heisst
r. Weiter sind beide Wellen im gleichen Medium
1, das heisst 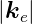 = ke =
= ke = 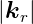 = kr. Wir können also
schreiben
= kr. Wir können also
schreiben
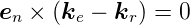 | (2.8) |
Mit Beträgen geschrieben heisst dies
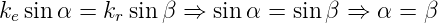 | (2.9) |
Dabei ist α der Winkel zwischen der Oberflächennormale 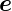 n
und dem Wellenvektor der einfallenden Welle
n
und dem Wellenvektor der einfallenden Welle 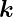 e und β der
Winkel zwischen der Oberflächennormale
e und β der
Winkel zwischen der Oberflächennormale 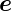 n und dem
Wellenvektor der reflektierten Welle
n und dem
Wellenvektor der reflektierten Welle 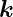 r.
r.
Das Reflexionsgesetz besagt, dass
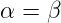 | (2.10) |
(Einfallswinkel=Ausfallswinkel)
Aus Gleichung (2.6) folgt weiter
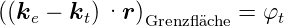 | (2.11) |
Gleichung (2.7) ist also die Gleichung einer Ebene, die
senkrecht zu 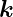 e −
e −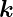 t liegt. Andererseits wissen wir, nach
unserer Konstruktion, dass
t liegt. Andererseits wissen wir, nach
unserer Konstruktion, dass 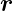 in der Grenzfläche mit dem
Normalenvektor
in der Grenzfläche mit dem
Normalenvektor 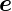 n liegt.
n liegt. 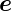 n ist also parallel zu
n ist also parallel zu 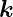 e −
e −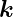 t. Wir
können also schreiben
t. Wir
können also schreiben
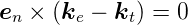 | (2.12) |
Mit Beträgen geschrieben heisst dies
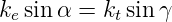 | (2.13) |
Dabei ist α der Winkel zwischen der Oberflächennormale 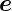 n
und dem Wellenvektor der einfallenden Welle
n
und dem Wellenvektor der einfallenden Welle 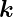 e und γ
der Winkel zwischen der Oberflächennormale
e und γ
der Winkel zwischen der Oberflächennormale 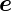 n und
dem Wellenvektor der transmittierten Welle
n und
dem Wellenvektor der transmittierten Welle 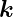 t. Aus der
Wellengleichung folgt
t. Aus der
Wellengleichung folgt
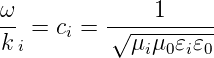 | (2.14) |
Da ωe = ωr = ωt ist, kann Gleichung (2.13) auch als
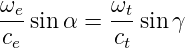 | (2.15) |
oder
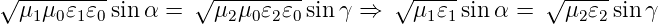 | (2.16) |
Mit der Definition (2.4) (n = 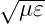 ) bekommt man
auch
) bekommt man
auch
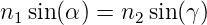 | (2.17) |
Dies ist das Brechungsgesetz nach Snellius.
Schliesslich können wir noch eine Beziehung der
Tangentialkomponenten aller Felder erhalten. Analog zur
Gleichung (2.3) können wir die Tangentialkomponenten der
Wellenvektoren angeben:
Wir subtrahieren Gleichung (2.18a) von Gleichung (2.18b),
beziehungsweise von Gleichung (2.18c).
Setzen wir mit Gleichung (2.8) für 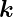 r −
r −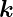 e = Γre
e = Γre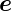 n und
n und
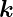 −
−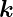 e = Γte
e = Γte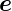 n erhalten wir
n erhalten wir
Die Tangentialkomponenten der Wellenvektoren der
einfallenden, reflektierten und gebrochenen Wellen sind
gleich.
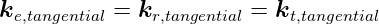 | (2.20) |
Die Änderung der Ausbreitungsrichtung bei Reflexion und
Brechung stammt alleine von den Komponenten der
Wellenvektoren, die parallel zum Normalenvektor der
Grenzfläche liegen.
2.3.1 s-Polarisation
|
|
| | Folien zur Vorlesung vom 16. 07. 2009 |
| | Aufgabenblatt 14 für das Seminar vom 22. 07. 2009 (Ausgabedatum 16. 07. 2009). |
| | |
|
|
| |
Zur Berechnung der Amplitude der reflektierten und
transmittierten Wellen mit einer allgemeinen Polarisation
verwenden wir zwei orthogonale Polarisationsrichtungen, die
s-Polarisation und die p-Polarisation. Jeder Polarisationszustand
kann als Linearkombination der s-Polarisation und der
p-Polarisation geschrieben werden.
Wir beginnen die Rechnungen für elektromagnetische
Wellen mit einer Polarisation senkrecht zur Einfallsebene
(s-Polarisation).
Wenn in den beiden angrenzenden Medien die
Dielektrizitätskonstanten 𝜀1 und 𝜀2 sind, dann muss der
Pointingvektor (Energiestrom) senkrecht zur Grenzfläche an
der Grenzfläche kontinuierlich sein, also
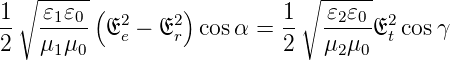 | (2.21) |
wobei α und γ die Winkel zur Oberflächennormalen 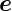 n
sind, Ee ist die Amplitude der
n
sind, Ee ist die Amplitude der 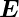 -Feldkomponente der
einfallenden elektromagnetischen Welle parallel zur Oberfläche
(s-Polarisation), Er die Amplitude der reflektierten und Et die
der gebrochenen elektromagnetischen Welle.
-Feldkomponente der
einfallenden elektromagnetischen Welle parallel zur Oberfläche
(s-Polarisation), Er die Amplitude der reflektierten und Et die
der gebrochenen elektromagnetischen Welle.
Die Komponente von 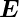 parallel zur Oberfläche muss stetig
sein, also ist nach Gleichung (2.3)
parallel zur Oberfläche muss stetig
sein, also ist nach Gleichung (2.3)
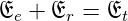 | (2.22) |
Aus der Kombination der Gleichungen (2.21) und
(2.22) erhalten wir die Fresnelschen Gleichungen für die
s-Polarisation.
Mit den Brechungsindizes n1 = 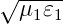 und n2 =
und n2 = 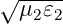 erhält man
erhält man
Nach dem Brechungsgesetz ist
Wir setzen dies ein und erhalten
Wir setzen Ee + Er = Et ein und bekommen die Fresnelsche
Formeln für die s-Polarisation
Dabei ist
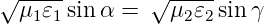
Für nichtmagnetische Materialien können die
Fresnelgleichungen für die s-Polarisation umgeschrieben
werden
Dabei ist
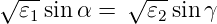
- Wenn α > γ, wenn also die elektromagnetische Welle
aus dem schnelleren Medium auf das langsamere
Medium trifft, haben Ee und Er unterschiedliche
Vorzeichen: es tritt ein Phasensprung um π bei der
Reflexion auf.
- Bei der Reflexion am schnelleren Medium α < γ ist
sin(α − γ) negativ und Er positiv. Es gibt keinen
Phasensprung bei der Reflexion. Dies erklärt zum
Beispiel, warum Seifenlamellen in Reflexion schwarz
werden, wenn die Dicke gegen null geht.
- Die Gesetze für die Intensität bekommt man
durch quadrieren und unter Berücksichtigung der
relativen Dielektrizitätszahl 𝜀1 und der relativen
magnetischen Permeabilität μ1.
- Bei fast senkrechtem Einfall bekommt man Er ≈
−Ee
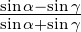 ≈−Ee
≈−Ee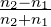
- und für die Transmission Et ≈ −Ee
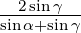 ≈
Ee
≈
Ee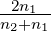
Die Fresnelsche Formeln für die Intensität bei der
s-Polarisation für nichtmagnetische Materialien lauten
Wir haben die einfallende Intensität Ie = n1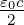 Ee2 als
Referenz verwendet. Deshalb erscheint der Vorfaktor
Ee2 als
Referenz verwendet. Deshalb erscheint der Vorfaktor 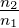 für It.
Im Medium mit dem Brechungsindex n2 wird die Energie mit
einer anderen Geschwindigkeit transportiert als im Medium
mit dem Brechungsindex n1. Ist n2 grösser als n1. so ist die
Ausbreitungsgeschwindigkeit kleiner und I2 muss grösser
werden.
für It.
Im Medium mit dem Brechungsindex n2 wird die Energie mit
einer anderen Geschwindigkeit transportiert als im Medium
mit dem Brechungsindex n1. Ist n2 grösser als n1. so ist die
Ausbreitungsgeschwindigkeit kleiner und I2 muss grösser
werden.
Bei fast senkrechtem Einfall erhalten wir
- für die Reflexion Ir ≈ I0
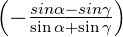 2 ≈
I0
2 ≈
I0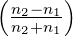 2
2
- und die Transmission It ≈ I0
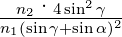 ≈
I0
≈
I0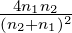 .
.
2.3.2 p-Polarisation
__________________________________________________________________________
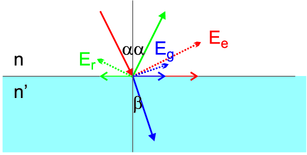
Stetigkeitsbedingungen für elektromagnetische Wellen mit
p-Polarisation. Die dicken Vektoren stellen die
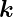 -Vektoren dar (rot für die einfallende
elektromagnetische Welle, grün für die reflektierte und
blau für die gebrochene elektromagnetische Welle.). Die
-Vektoren dar (rot für die einfallende
elektromagnetische Welle, grün für die reflektierte und
blau für die gebrochene elektromagnetische Welle.). Die
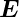 -Vektoren sind gestrichelt gezeichnet, ihre Projektion
auf die Grenzfläche dünn.
-Vektoren sind gestrichelt gezeichnet, ihre Projektion
auf die Grenzfläche dünn.
_____________________________________________________________________
Bei p-polarisierten elektromagnetischen Wellen ist die
Bedingung für die Stetigkeit der Parallelkomponente von 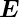 durch
durch
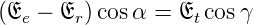 | (2.29) |
gegeben. Weiter gilt immer noch die Beziehung für den
Poynting-Vektor (Energieerhaltung)
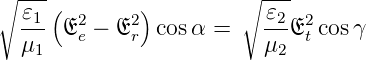 | (2.30) |
Wir teilen die beiden Gleichungen und lösen das
Gleichungssystem und erhalten die Fresnelsche Formeln
(p-Polarisation):
Für nichtmagnetische Materialien vereinfachen sie sich
unter Verwendung der Brechungsindizes zu
Bei senkrechtem Einfall gilt cos α ≈ cos γ ≈ 1 und damit
- für die Reflexion Er ≈Ee
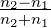
- und für die Transmission Et ≈Ee
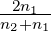
Dass das Vorzeichen von Er anders ist als bei der s-Polarisation
hängt mit der Definition der lokalen Koordinatensystem der
reflektierten Wellen zusammen und ist kein Wiederspruch.
Die Brechungsindizes n1 und n2 können mit dem
Snelliusschen Gesetz n1 sin α = n2 sin γ eliminiert werden
Die Fresnelschen Formeln für die Intensität bei
nichtmagnetischen Materialien lauten
Wir haben die einfallende Intensität Ie = n1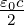 Ee2 als
Referenz verwendet. Deshalb erscheint der Vorfaktor
Ee2 als
Referenz verwendet. Deshalb erscheint der Vorfaktor 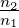 für
It.
für
It.
Bei senkrechtem Einfall erhalten wir
- für die Reflexion Ir ≈I0
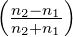 2
2
- und die Transmission It = I0
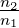
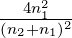 = I0
= I0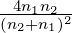 .
.
2.3.3 Grenzfall des senkrechten Einfalles
Im Grenzfall α → 0 stimmen die Resultate für die s- und
p-Polarisation überein. In diesem Falle ist
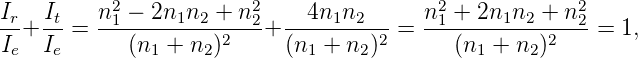 | (2.35) |
also ganz klar die Energie erhalten. Der Faktor n2∕n1 ist
notwendig dazu.
2.3.4 Brewster-Winkel
Wenn bei der p-Polarisation in der Gleichung (2.33) für Er der
Nenner α + γ(α) = π∕2 ist, divergiert er. Wir erhalten also
Er(α = π∕2 −γ(α)) = 0. Dies ist der Brewster-Winkel. Beim
Brewsterwinkel gegeben durch α + γ(α) = π∕2 ist Er,p für die
p-Polarisation gleich null. Die elektromagnetische Welle ist
s-polarisiert!
Mit dem Snelliusschen Brechungsgesetz folgt
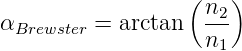 | (2.36) |
__________________________________________________________________________
Polarisation bei der Spiegelung an Wasser. Links ist der
Analysator so gestellt, dass dass das an der
Wasseroberfläche reflektierte Licht durchgelassen wird.
Rechts die gleiche Szene, aber der Analysator blockt das
an der Wasserfläche reflektierte Licht.
_____________________________________________________________________
_____________________________________________________________________
Polarisation bei der Spiegelung an Wasser. Die beiden
Bilder aus Abbildung 2.3.4 sind hier
übereinandergelegt.Die Trennlinie läuft entlang des
Baumstammes.
_____________________________________________________________________
_____________________________________________________________________
Polarisation bei der Spiegelung an Wasser. Linkes und
rechtes Bild wurden mit zwei Stellungen des
Polarisationsfilters aufgenommen.
_____________________________________________________________________
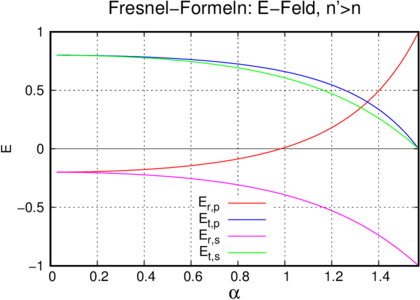
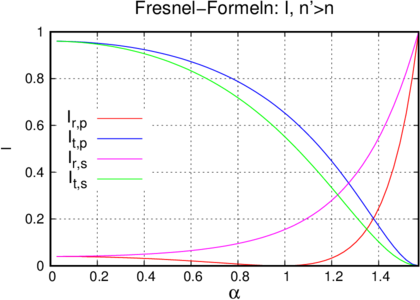
2.3.5 Beispielkurven für die Fresnelformeln
__________________________________________________________________________
Verlauf der Amplitude des elektrischen Feldes (links)
und der Intensität(rechts) für p- und s-Polarisation,
wenn elektromagnetische Wellen aus dem schnelleren
Medium (n1 = 1) in das langsamere (n2 = 1.5) eintreten.
Die Intensität ist mit I = niE2 berechnet worden, wobei
ni die für das jeweilige Medium gültige Brechzahl ist.
_____________________________________________________________________
_____________________________________________________________________
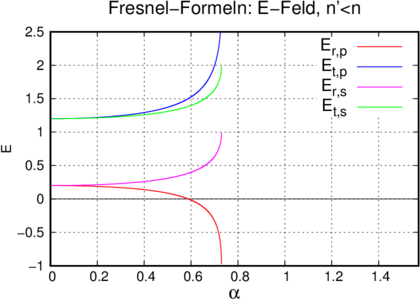
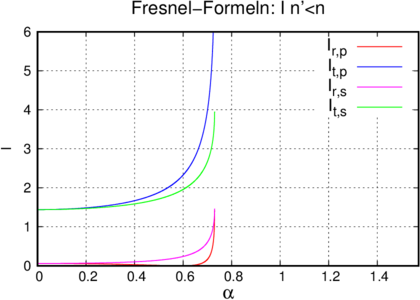
Verlauf der Amplitude des elektrischen Feldes (links)
und der Intensität(rechts) für p- und s-Polarisation,
wenn elektromagnetische Wellen aus dem langsameren
(n1 = 1.5) Medium in das schnellere (n2 = 1) eintreten.
Die Intensität ist mit I = niE2 berechnet worden, wobei
ni die für das jeweilige Medium gültige Brechzahl ist.
_____________________________________________________________________
2.3.6 Evaneszente Wellen
(Siehe Hecht, Optik [Hec05, pp. 193,196])
Aus den letzten Abbildungen ist ersichtlich, dass, wenn
elektromagnetische Wellen aus dem langsameren Medium (n1)
in das schnellere n2 < n1 eintreten, es Winkel γ gibt
((n1∕n2) sin α = sin γ > 1), für die es keine reelle Lösung
der Fresnelschen Formeln gibt. Die Lösung ist dann in
die z-Richtung rein imaginär. Dies heisst, dass auch die
z-Komponente des 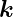 -Vektor der elektromagnetischen Welle
im schnelleren Medium imaginär wird. Darum wird aus eikzz
mit kz = iκz der exponentielle Dämpfungsfaktor e−κzz, wobei
κz vom Einfallswinkel abhängt. Die elektromagnetischen
Wellen aus dem langsameren Medium können sich im
schnelleren Medium also nicht weiter in die z-Richtung
bewegen: Wegen der Energieerhaltung ist die Reflexion
perfekt.
-Vektor der elektromagnetischen Welle
im schnelleren Medium imaginär wird. Darum wird aus eikzz
mit kz = iκz der exponentielle Dämpfungsfaktor e−κzz, wobei
κz vom Einfallswinkel abhängt. Die elektromagnetischen
Wellen aus dem langsameren Medium können sich im
schnelleren Medium also nicht weiter in die z-Richtung
bewegen: Wegen der Energieerhaltung ist die Reflexion
perfekt.
Eine kurze Rechnung zeigt,
dass im Falle der Totalreflexion (n1 sin(α) ≥n2 und damit
n22 −n
12 sin 2(α) ≤ 0) der Betrag von 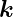 t,senkrecht
t,senkrecht
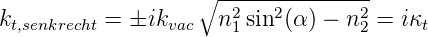 | (2.37) |
ist. Die physikalisch sinnvolle Lösung für einen unendlich
ausgedehnten Halbraum mit dem Brechungsindex n2 ist die
exponentiell abfallende Lösung
 | (2.38) |
Die resultierende Welle im Medium 2 hat dann die
zeitgemittelte Intensität
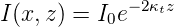 | (2.39) |
Wir erhalten also für die Intensität einen exponentiellen
Abfall mit einer Abfalllänge
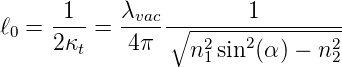 | (2.40) |
Wenn eine Welle mit der Vakuumwellenlänge λvac = 500 nm
und dem Einfallswinkel α = 5π∕12 = 75° von einem Medium
mit dem Brechungsindex n1 = 1.55 in Luft n2 = 1 übertritt,
ist λ0 = 35.71 nm.
[Nächste Seite] [Vorherige Seite] [vorheriges Seitenende]
[Seitenanfang] [Ebene nach oben]
©2002-2017 Ulm
University, Othmar Marti,  Lizenzinformationen
Lizenzinformationen



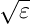
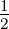
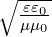
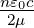
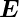
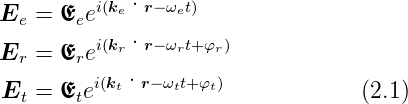
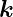
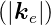 . An den
Grenzflächen gilt
. An den
Grenzflächen gilt 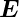 ist stetig.
ist stetig.
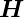 ist stetig.
ist stetig.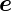
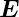
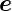
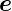
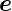
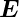
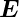
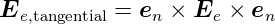
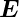
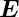
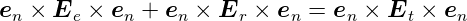
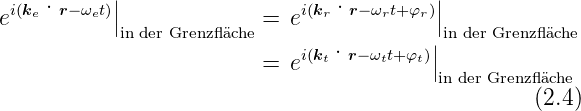
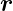 nach Definition ein Vektor in der Grenzfläche ist,
also mit
nach Definition ein Vektor in der Grenzfläche ist,
also mit 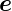
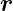
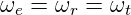
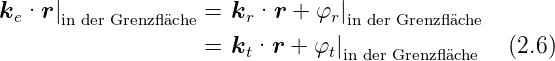
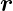 zeigt auf einen Punkt in der Grenzfläche. Da der Ursprung
des Koordinatensystems nicht in der Grenzfläche liegen muss,
ist
zeigt auf einen Punkt in der Grenzfläche. Da der Ursprung
des Koordinatensystems nicht in der Grenzfläche liegen muss,
ist 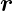 im Allgemeinen nicht parallel zur Grenzfläche. Aus der
ersten Gleichung in (
im Allgemeinen nicht parallel zur Grenzfläche. Aus der
ersten Gleichung in (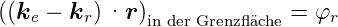
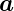
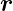
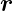 liegen in der Ebene mit dem
Normalenvektor
liegen in der Ebene mit dem
Normalenvektor 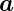 .
. 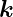
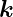
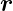 in der Grenzfläche
mit dem Normalenvektor
in der Grenzfläche
mit dem Normalenvektor 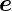
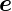
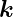
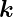
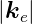
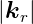
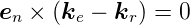
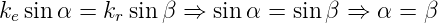
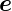
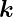
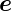
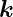
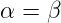
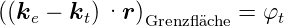
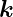
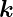
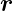 in der Grenzfläche mit dem
Normalenvektor
in der Grenzfläche mit dem
Normalenvektor 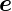
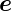
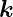
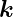
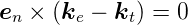
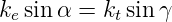
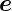
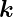
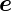
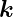
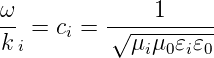
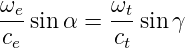
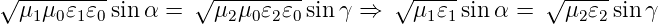
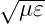 ) bekommt man
auch
) bekommt man
auch
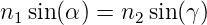
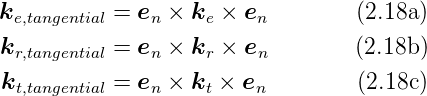
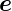
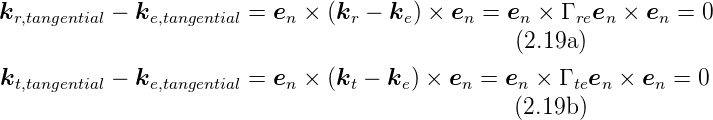
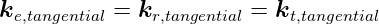
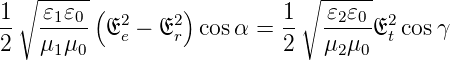
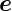
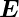 -Feldkomponente der
einfallenden elektromagnetischen Welle parallel zur
-Feldkomponente der
einfallenden elektromagnetischen Welle parallel zur 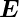 parallel zur
parallel zur 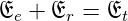
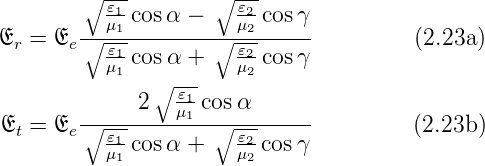
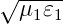 und
und 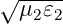 erhält man
erhält man
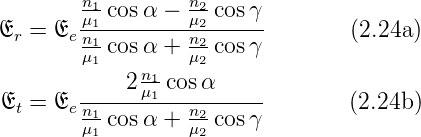
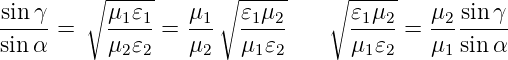
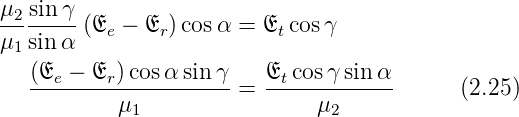
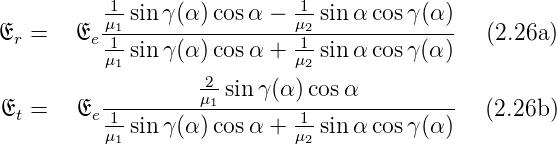
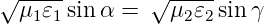
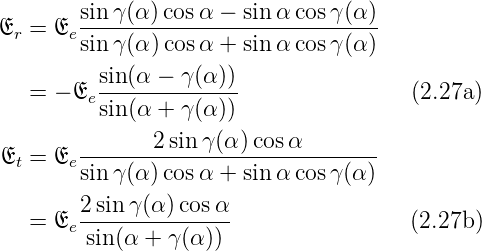
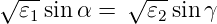
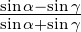
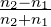
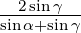
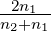
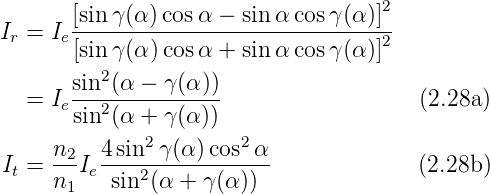
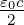
 für
für 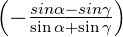
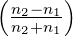
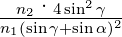
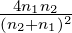 .
.
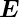 durch
durch
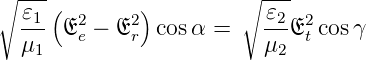
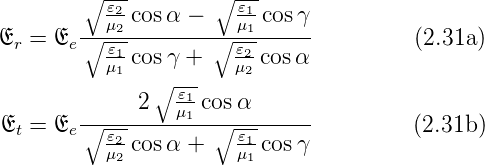
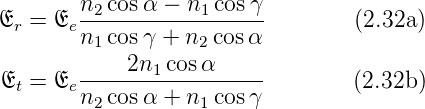
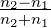
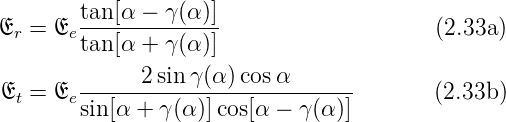
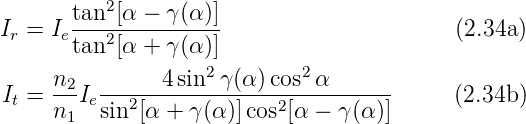
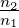 für
für
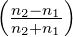
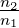
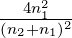
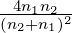 .
.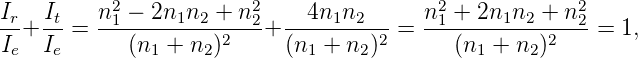





 -Vektor der elektromagnetischen Welle
im schnelleren Medium imaginär wird. Darum wird aus
-Vektor der elektromagnetischen Welle
im schnelleren Medium imaginär wird. Darum wird aus 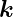
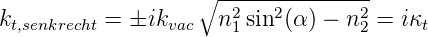

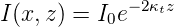
 Lizenzinformationen
Lizenzinformationen