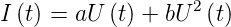
Um Signale über grössere Distanzen transportieren zu können, wird das Nutzsignal oft auf einen Träger aufmoduliert. Grob gesagt, kann man so ein Signal in einem Bereich mit schlechten Ausbreitungseigenschaften in einen Bereich mit längerreichweitiger Übertragungsmöglichkeit transferieren. Oder es können in einem Kabel mehrere bis sehr viele Telefongespräche gleichzeitig geführt werden. Modulation tritt auf, wenn zwei oder mehrere Signale mit unterschiedlichen oder gleichen Frequenzen durch ein nichtlineares Bauteil laufen. Liegen an einer Strecke mit der Strom-Spannungscharakteristik
|
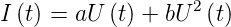| (2.1) |
die zwei Signale U1 = Û1 cos ω1t und U2 = Û2 cos ω2t an, dann treten Terme bei den Summen- und Differenzfrequenzen auf. Man beachte, dass mit reellen Grössen gerechnet werden muss. Werden die bequemen komplexen Darstellungen verwendet, muss immer auch das konjugiert-komplexe mitgenommen werden, also effektiv auch eine reelle Zahl. Wir erhalten also
neben den beiden ursprünglichen Signalen treten auch ein Gleichstromanteil sowie die doppelten, die Summen- und die Differenzfrequenzen auf. Eine Nichtlinearität von höherer Ordnung würde entsprechend den Produkt- und Summenregeln für Winkelfunktionen noch mehr Frequenzen ergeben.
Die oben gezeigte Rechnung illustriert die Amplitudenmodulation. Allgemein kann man schreiben:
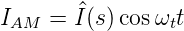 | (2.3) |
ωt ist die Trägerfrequenz. Î(s) hängt nun vom aufmodulierten Signal ab:
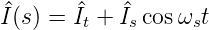 | (2.4) |
Ît ist die Intensität des Trägers, Îs diejenige des
aufmodulierten Signals mit der Frequenz ωt. Typischerweise
ist ωs «ωt. Mit der Abkürzung m =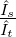 
ergibt sich
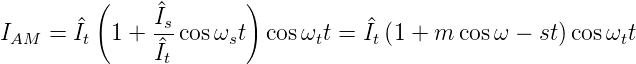 | (2.5) |
m heisst auch der Modulationsgrad. Anwendung der Additionssätze für Winkelfunktionen ergibt:
![^
IAM = I^tcos ωtt + Itm--[cos (ωt − ωs)t + cos(ωt + ωs)t]
2](phys_elektr517x.png) | (2.6) |
Das resultierende Signal enthält also sowohl die Summen- wie auch die Differenzfrequenzen. man ersieht aus der Herleitung, dass man zwar für eine Amplitudenmodulation eine quadratisch-nichtlineare Kennlinie nehmen könnte, dass es aber geschickter ist, einen Multiplizierer zu verwenden. Weiter ersieht man, dass um ein Signal der Frequenz ωs zu übertragen, man eine Bandbreite
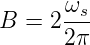 | (2.7) |
benötigt wird. Gleichung (2.6) zeigt weiter, dass bei einem Modulationsgrad von 1 die Hälfte der Sendeenergie im Träger steckt und dass je ein Viertel in den beiden Seitenbändern vorhanden ist. Für eine Radioübertragung ist aber nur der Energiegehalt in den Seitenbändern wichtig. Deshalb gibt es Sendeverfahren, bei denen der Träger unterdrückt oder sogar mit dem Träger das eine Seitenband nicht gesendet wird. Die Stereoinformation bei einer Stereo-UKW-Sendung wird mit diesem Verfahren bandbreitensparend übertragen. Zur Wiederherstellung des Signals benötigt man den träger. Sind beide Seitenbänder vorhanden, kann man einen Oszillator im Mittel mit dem Signal mitlaufen lassen (das Signal hat, gemittelt, gerade die Trägerfrequenz). Bei Einseitenbandmodulation (SSB für Single Sideband Modulation) verwendet man entweder einen Pilotton (UKW-Stereo) oder man ist darauf angewiesen, das der Sender und der Empföänger sehr stabil laufen. Als Kuriosum sei erwähnt, dass eine Möglichkeit Sprache zu verschlüsseln, darin besteht, das Sprachsignal in Bänder aufzuteilen und mit SSB in der Frequenz zu verschieben. Die Frequenzverschiebung kann auch dynamisch sein.
Die Amplitudenmodulation ist eher störanfällig. Deshalb werden qualitativ hochwertigere Dienste mit Frequenzmodulation ausgestrahlt. Die Trägerfrequenz ωt wird mit der Signalfrequenz ωs moduliert. Das heisst, die Phase des Signals bewegt sich nicht mehr mit konstanter Geschwindigkeit. Also schreibt man anstelle von ωt = φ, der phase, das Integral
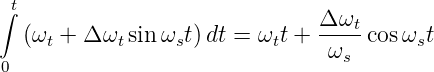 | (2.8) |
Δωt ist der Frequenzhub der Modulation. Das frequenzmodulierte Signal ist also:
Die Amplituden În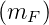
der einzelnen Teilfrequenzen
ωt + nωs sind Bessel-Funktionen n-ter Ordnung. das
Argument mF = 
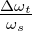. Man benötigt für die FM-Übertragung
eine Bandbreite von
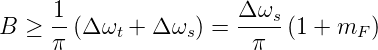 | (2.10) |
Der Frequenzhub bei der FM hängt nicht von der Signalfrequenz, sondern nur von der Amplitude ab. Anstelle der Frequenz kann man auch die Phase modulieren. Das Signal sieht dann folgendermassen aus:
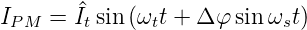 | (2.11) |
Hier hängt der Phasenhub von der Amplitude ab, der resultierende Frequenzhub ist aber durch die Signalfrequenz bestimmt.
Lizenzinformationen
![( ) ( )2
I (t) = a U^1 cosω2t + U^2 cosω2t + b ^U1 cosω2t + ^U2 cosω2t
= a^U1cos ω2t + a^U2 cosω2t +
bU^2 cos2ω t + b^U2 cos2ω t + 2b^U U^ cosω tcosω t
(1 1 ) 2 2 1 2 1 2
= b- ^U2 + ^U 2 +
2 1 2
a^U1cos ω2t + a^U2 cosω2t +
b( )
-- ^U21 cos2ω1t + ^U 22 cos2 ω2t +
2
bU^1 ^U2 [cos (ω1 − ω2)t + cos(ω1 + ω2)] (2.2)](phys_elektr512x.png)
