| Abbildung 3.87.: | Théveninsche Ersatzschaltung (gezeichnet nach [HH89]). |

Passive Bauelemente besitzen keine eingebaute Leistungsquelle; ihre Ausgangsleistung kann also niemals grösser als ihre Eingangsleistung sein. (Wohl aber kann die Ausgangsspannung grösser als die Eingangsspannung sein, siehe Transformator.) Passive Bauelemente sind stets zweipolig. Lineare Zweipole verknüpfen ein Eingangssignal linear mit dem zugehörigen Ausgangssignal. Dem wichtigsten nichtlinearen Zweipol — der Diode — widmen wir einen eigenen Abschnitt im Anschluss.
In einem Gleichstromkreis gibt es neben Spannungs- und Stromquellen nur Widerstände (> 0Ω bis < ∞Ω); Kondensatoren und Spulen sind erst in Wechselstromkreisen wirksam. Im erweiterten Sinn sind auch Schalter, Relais, Verbinder, etc. sowie Messgeräte Zweipole.
Zur Erinnerung: Zum Repertoire zur Beschreibung von Zweipolschaltungen gehören das ohmsche Gesetz, die Begriffe Spannung, Strom, Leistung, die Knoten– und Maschenregel (Kirchhoffschen Gesetze), die Formeln für Serien– und Parallelschaltungen von Widerständen und für den Spannungsteiler.
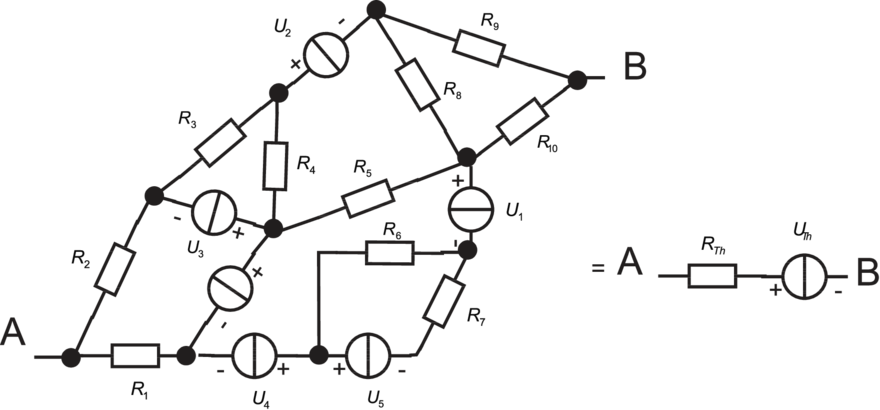
Die Untersuchung eines Netzwerkes aus Widerständen und Spannungsquellen kann sehr mühselig sein. Aber sie ist beispielsweise notwendig, wenn es um die ‘Belastung’ einer Schaltung geht. Ein einfaches Beispiel hierfür ist der belastete Spannungsteiler, siehe Abbildung 3.88.
Zwei Theoreme helfen dabei:
Das Theorem nach Thévenin sagt aus, dass jedes Netzwerk aus
Zweipolen, z. B. aus Spannungsquellen und Widerständen,
äquivalent durch eine Ersatzschaltung aus einer (idealen)
Spannungsquelle mit UTh und einem (inneren) Widerstand
RTh in Reihe beschreibbar ist.
Zur Berechnung der Théveninschen Ersatzschaltung geht man folgendermassen vor:
Das Theorem von Norton besagt das gleiche für eine Ersatzschaltung aus einer (idealen) Stromquelle und einem parallelen Widerstand. Hier geht man wie folgt vor:
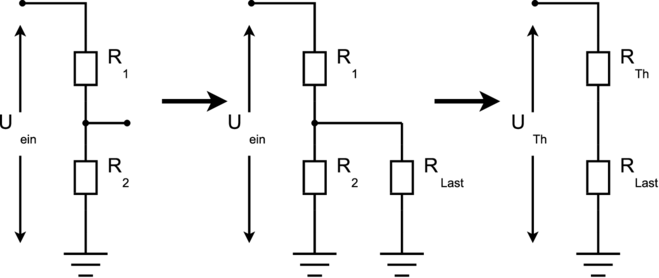
| Abbildung 3.88.: | Unbelasteter und belasteter Spannungsteiler nebst seiner Théveninschen Ersatzschaltung (gezeichnet nach Horowitz/Hill [HH89]). |
UTh ist die Leerlaufspannung sowohl der Ersatzschaltung als auch des äquivalenten Schaltnetzwerks und kann berechnet oder gemessen werden. Der Kurzschlusstrom im geschlossenen Ersatzkreis ist gleich dem Kurzschlussstrom im äquivalenten Netzwerk, also

Das Bild von einem äquivalenten Innenwiderstand ist nicht nur auf die Spannungsquelle ‘Spannungsteiler’ beschränkt, sondern wird ebenso auf Batterien, Oszillatoren, Verstärker und Sensoren angewand. Die Ausdrücke Quellenwiderstand, Innenwiderstand, Ausgangswiderstand und Théveninscher Ersatzwiderstand meinen alle dasselbe.
Müssen Kondensatoren und Spulen berücksichtigt werden, so gilt das Thévenin–Theorem in verallgemeinerter Form: Jedes Zweipol–Netzwerk aus Widerständen, Kondensatoren, Spulen und Signalquellen ist äquivalent einer einzigen komplexen Impedanz in Serie mit einer einzigen Signalquelle. Die Ersatzspannungsquelle und die Ausgangsimpedanz werden wie oben ermittelt.
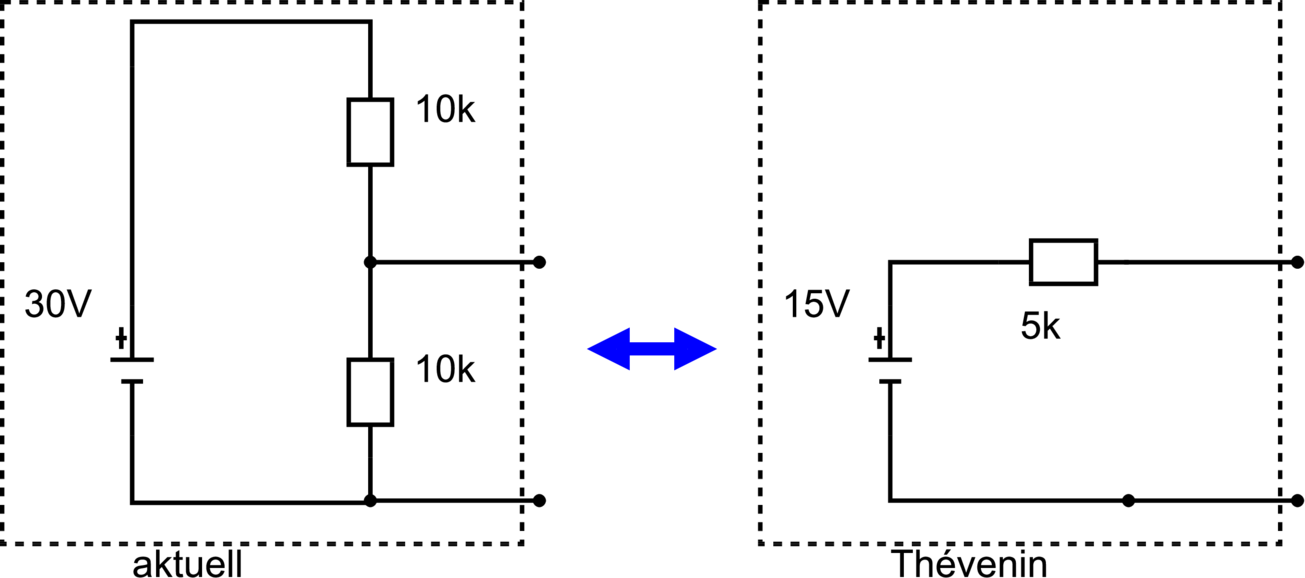
| Abbildung 3.89.: | Beispiel für die Ersatzschaltung eines Spannungsteilers (gezeichnet nach Horowitz/Hill [HH89]). |
Übungsaufgabe: Berechnen Sie UTh und RTh für den Fall, dass die Widerstände 100kΩ, 1MΩ, 100MΩ betragen.
Eine wichtige Anwendung des Théveninschen Modells ist die Vorhersage der Ausgangsspannung einer Spannungsquelle (z. B. der genannte Spannungsteiler) oder einer ganzen Schaltungsgruppe unter Last. Noch allgemeiner: Wenn ein Schaltkreis A einen Schaltkreis B ansteuert, — also mit ihm belastet wird — in welchem Verhältnis muss der Ausgangswiderstand von A zum Eingangswiderstand von B stehen, damit der Spannungseinbruch von A einen gewünschten Prozentsatz nicht übersteigt? Die Betrachtung folgt immer dem selben Weg: erst ermittelt man die beiden Elemente UTh und RTh der Ersatzschaltung für Schaltkreis A, dann betrachtet man den Spannungsteiler unter Berücksichtigung des Eingangswiderstands des Schaltkreises B als Last. Sukzessive können so weitere Lasten angehängt werden.
Für die Praxis gilt folgende Merkregel: Um den Spannungseinbruch einer Quelle klein zu halten, sollte der Lastwiderstand möglichst gross gehalten werden. Es sollte gelten:
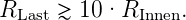 | (3.1) |
Bei Anwendungen in der Hochfrequenztechnik (‘reflexionsfreie Anpassung’) oder zur optimalen Leistungsanpassung gilt aber stets:
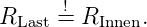 | (3.2) |
Die physikalischen Grundlagen der Dioden wurden bereits in Kapitel 3.2 ausführlich behandelt. Es folgen hier einige praxisbezogene Bemerkungen.
Diskrete Dioden haben stets zwei Anschlüsse: Anode (A) und Kathode (K); integrierte Dioden besitzen noch einen dritten Anschluss (Substratanschluss S). Die Gehäuseformen von Einzeldioden ähneln denen von Widerständen, der Farbring kennzeichnet die Kathode. Weitere Formen, insbesondere Leistungsdioden.
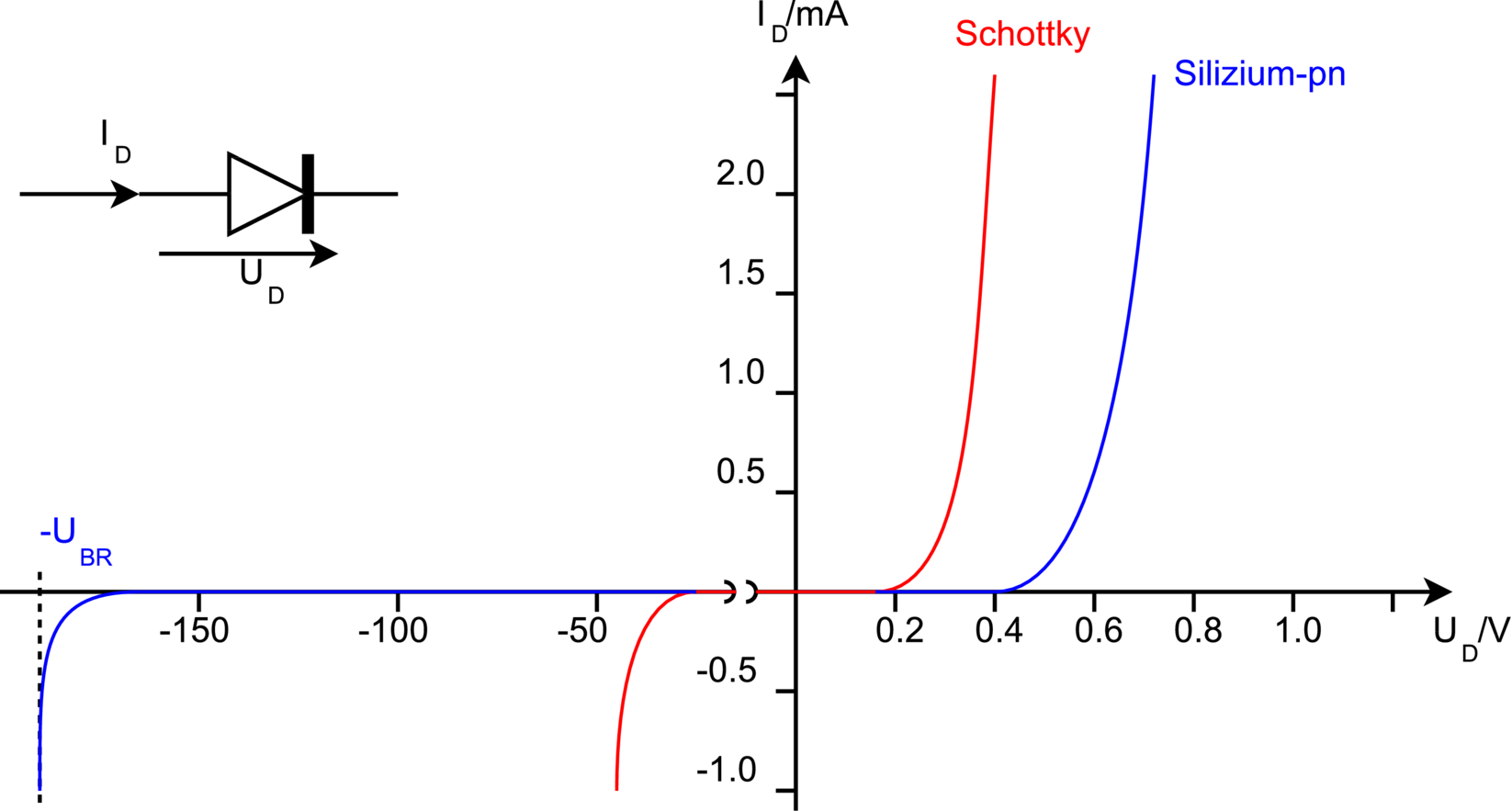
| Abbildung 3.91.: | Kleinsignal–Diode: Strom–Spannungs–Kennlinien (gezeichnet nach Tietze/Schenk[TS99]). |
Die in Abbildung 3.92 gezeigten Kennlinien geben nochmals die drei Betriebsbereiche wieder: Durchlass–, Sperr– und Durchbruchsbereich. Im Durchlass beträgt die sog. Flussspannung UF (forward voltage) bei typischen Betriebsströmen bei Ge– und Schottkydioden ca. 0, 3 −0, 4V, bei Si–Dioden ca. 0, 6 −0, 7V. Dieser ‘Durchlass–Spannungsabfall’ ist annähernd konstant; ein Fakt, der die Diskussion von Schaltungen mit Dioden ganz wesentlich vereinfacht. Für eine erste Betrachtung kann er häufig ganz vernachlässigt werden. Für hohe Diodenströme ID sind die Durchlasswiderstände sehr klein: RD ≈ 0, 01 −10Ω.
Umgekehrt sind die Sperrwiderstände RS sehr hoch, bei Si i. allg. > 10MΩ. Die zugehörigen Sperrströme IR (reverse current) sind extrem klein, meist < 10−7A. Schliesslich wird die Sperr–Durchbruchspannung UBR (peak inverse voltage) erreicht, die meist bei einigen 10 V liegt, aber auch 1 kV bei Stromgleichrichterdioden betragen kann. Ausser bei Zenerdioden sollte diese Sperrspannung keinesfalls erreicht werden. In einer ersten Schaltungsbetrachtung haben die Dioden in Sperrrichtung einen ∞–grossen Widerstand.
Das dynamische Verhalten von Dioden wurde bereits in Kapitel 3.2 prinzipiell diskutiert. In der Praxis spielt das Schaltverhalten bei ohmscher bzw. ohmsch–induktiver Last und bei höheren Frequenzen eine entscheidende Rolle. In Durchlassrichtung stellen sich konstante Betriebsbedingungen meist in wenigen Nanosekunden ein, in Sperrrichtung werden ähnliche Werte für die Abfallzeiten nur bei Schottkydioden mit kleineren Kapazitäten erreicht, Siliziumdioden wie die 1 N 4148 Kleinsignaldiode benötigen ca. 100 μs, bei Stromgleichrichterdioden werden mehrere μs benötigt. Weitere Informationen.
CAD–Programme zur Schaltungssimulation wie z. B. PSPICE verwenden nichtlineare Diodenmodelle mit den Grössen für den Diffusions–, Rekombinations– und Durchbruchstrom, für den Bahnwiderstand und für die Sperrschicht– und Diffusionskapazitäten. Zahlreiche Parameter charakterisieren das statische, dynamische und thermische Verhalten. Muss man auf die Hilfe von Computern verzichten, helfen linearisierte Kleinsignalmodelle, die im Wesentlichen den differentiellen Diodenwiderstand und die beiden Kapazitäten in einem Arbeitspunkt berücksichtigen.
Es gibt eine Vielzahl von Dioden–Anwendungen. Einer der wichtigsten ist die Gleichrichtung von Wechselspannungen, d. h. der periodische Wechsel von Durchlass– und Sperrbetrieb (‘Gleichrichterdiode’). Am einfachsten geschieht dies in Spannungsteilern; Abbildung 3.92 zeigt neben dem bekannten Einweg– oder Halbwellengleichrichter zwei verwandte Schaltungen, nämlich sog. Klemmen.
Am Eingang wird jeweils eine (ausreichend niederfrequente) Wechselspannung von V P−P = 20V angelegt. Am Ausgang des Einweggleichrichters beobachtet man die von der Diode durchgelassene, positive Halbwelle, reduziert um UF ≈ 0, 6V. Bei der linken Klemme sperrt die Diode bei der positiven Halbwelle, d. h. weil der Diodenwiderstand RS »R ist, fällt fast die gesamte Spannung am Ausgang an. In der negativen Halbwelle ist die Diode duchlässig, jetzt ist R »RD; am Ausgang liegt praktisch UF ≈ 0, 6V an. Die Klemme ‘klemmt’ die negative Ausgangsspannung auf −0, 6V. Die Klemme rechts ist erweitert worden um eine vorgespannte zweite Diode. Solange die positive Halbwelle Werte von U < 5V annimmt, sperrt die Diode 2. Für U > 5, 6V ist die Diode 2 sehr niederohmig, die Diode 1 aber extrem hochohmig; die zusätzliche Gleichspannung klemmt den maximalen positiven Spannungswert am Ausgang auf 5, 6V.
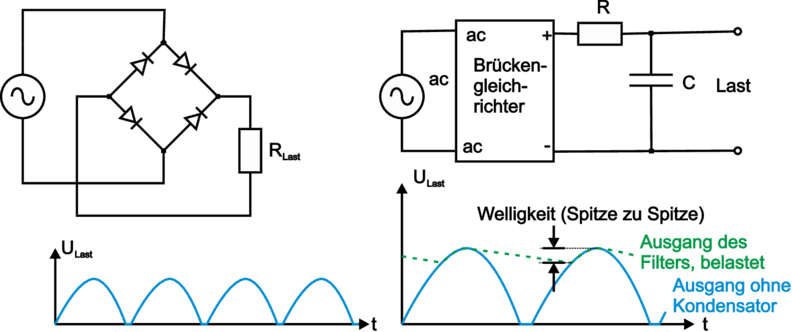
| Abbildung 3.93.: | Zweiweg–Brückengleichrichter links ohne und rechts mit Glättungs–Kondensator (gezeichnet nach Horowitz/Hill [HH89]). |
Vollwellen– oder Zweiweg–Brückengleichrichter nützen beide Halbwellen aus, siehe Bild 3.93. Allerdings fällt pro Halbwelle an zwei Dioden UF ab. Ein erster Schritt zum Einsatz als Netzgerät ist die Hinzunahme eines Glättungskondensator mit RLastC » 1∕f, wobei f die Brummfrequenz, also die doppelte Netzfrequenz meint. Die Brücke ist heutzutage ein kleines, integriertes Bauteil. Damit die Restwelligkeit kleiner und der Kondensator nicht zu gross und teuer werden muss, lässt man der obigen Anordnung ein weiteres integriertes Bauteil, einen sog. Spannungsregler folgen. Diese benutzen eine aktive Rückkopplungsschaltung; ein Prinzip, das wir bei den Operationsverstärkern erstmals kennenlernen werden.
Übungsaufgabe: Die Stromkennlinie Iaus(Iein) zeigt einen linearen, symmetrischen Verlauf. Tut dies die Spannungskennlinie Uaus(Uein) auch?
Die bisher besprochenen Anwendungen betrafen Kleinsignaldioden bzw. zumeist Netzgleichrichterdioden. Es gibt noch eine ganze Reihe spezieller Dioden, die für spezielle Anwendungen optimiert werden.
Zenerdioden werden im Sperrbereich betrieben; genauer, man nützt ihr Verhalten im Durchbruch. Abbildung 3.94 mit typischen Durchbruchkennlinien zeigt, dass Dioden mit kleineren Durchbruchspannungen noch nicht ganz ideal schalten. Die Anwendung im Spannungsteiler ist die Spannungsbegrenzung bzw. bei belastetem Spannungsteiler die Spannungsstabilisierung.
Kapazitätsdioden (Abstimmdioden, varicap) werden ebenfalls in Sperrrichtung betrieben. Man nützt die Spannungsabhängigkeit der Sperrschichtkapazität aus. Durch sog. hyperabrupte Dotierung (inhomogene, zur Grenzschicht hin ansteigende Konzentration) erreicht man Kapazitätskoeffizienten bis 1 und Kapazitätsvariationen bis Faktor 10. Die Anwendung liegt insbesondere in der Frequenzabstimmung von LC–Kreisen (z. B. im Radio) in Wobbelsendern oder zur Frequenzmodulation; hierzu sind meist 2 oder 3 Abstimmdioden in einem Gehäuse untergebracht.
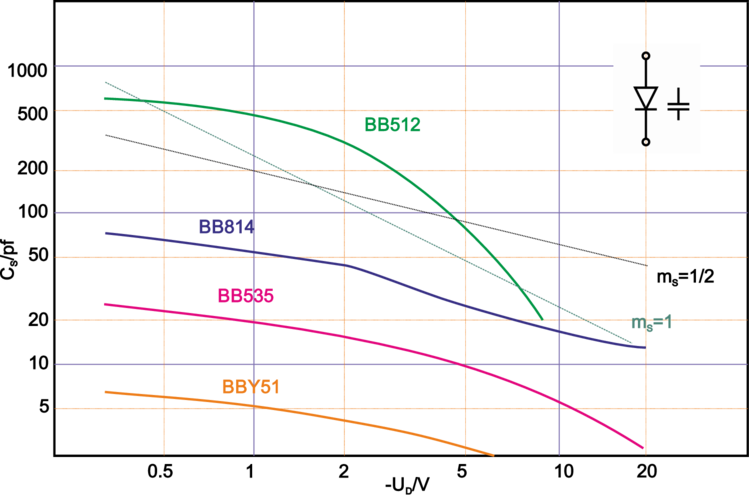
| Abbildung 3.95.: | Schaltzeichen und spannungsabhängige Kapazitäten an typischen Kapazitätsdioden (skizziert nach Tietze/Schenk [TS99]). |
Auf den negativen Widerstand von Esaki–Tunnel–Dioden wurde bereits hingewiesen. Sie finden in GHz–Oszillatoren und schnellen Schaltern ihre Verwendung.
Schaltdioden sind durch kleine Sperrkapazitäten und sehr steile Durchlasskennlinien ausgezeichnet. Sie werden als elektronische Schalter zum Ersatz von mechanischen Schaltern eingesetzt.
Schottky–Dioden (Mikrowellendioden, hot carrier diodes) haben kleine UF ≈ 0, 4V und können als Mikrowellendiode sehr kleine Kapazitäten aufweisen. Sie werden für Frequenzen > 15GHz als Mischer und Detektoren eingesetzt, sowie als sehr schneller Schalter. Vergleiche Datenblätter und Praktikum (Ringmischer).
Als PIN–Dioden (current–controlled RF–resistor) bezeichnet man Dioden mit geringer Störstellendichte und deshalb hoher Lebensdauer der Ladungsträger in der intrinsischen Schicht. Solche Dioden sperren zuverlässig nur bei relativ kleinen Frequenzen. Bei ca. f > 10MHz kann man die Dioden als gleichstromgesteuerten Wechselspannungswiderstand einsetzen, z. B. in HF–Dämpfungsgliedern.
Transistoren sind die wichtigsten aktiven Bauelemente. Ihre Ausgangsleistung kann grösser sein als ihre Eingangsleistung: Transistoren verstärken und können deshalb (durch Rückkopplung) der aktive Teil eines Oszillators sein. Die zusätzliche Leistung liefert eine ‘externe’ Quelle.
Transistoren sind praktisch in jeder elektronischen Schaltung enthalten; in IC’s findet man z. B. ca. 20 Transistoren in einer einfachen Operationsverstärkerschaltung oder in höchstintegrierten DRAM’s, Mikroprozessoren oder Logigschaltungen heute weit über 100 Millionen. Entsprechend ihrer Beschaltung werden, wie in den vorigen Abschnitten gezeigt, eine Vielzahl von Bauformen entwickelt.
Im Folgenden betrachten wir Einzeltransistoren und ihre Schaltungen.
Allen Bipolartransistoren sind einige für die praktische Anwendung relevante Eigenschaften gemeinsam. Meist werden sie im Normalbetrieb (forward region) eingesetzt. Das heisst, die Basis–Emitter–Diode wird in Durchlassrichtung und die Basis–Kollektor–Diode in Sperrrichtung betrieben. Dies gilt für npn– und pnp–Transistoren gleichermassen, mit vertauschten Vorzeichen für Ströme und Spannungen.
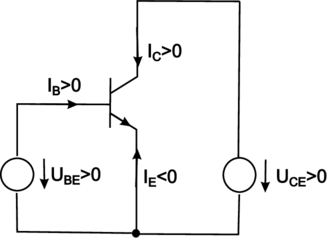
| Abbildung 3.96.: | Spannungen und Ströme eines npn–Transistors in Normalbetrieb (gezeichnet nach Tietze/Schenk [TS99]. |
Das Verhalten des jeweiligen Transistortyps beschreiben die sog. Kennlinienfelder, die in den zugehörigen Datenblättern gezeigt werden. Die Kennlinien sind immer nichtlinear oder nur abschnittsweise linear. Es gelten die Gleichungen
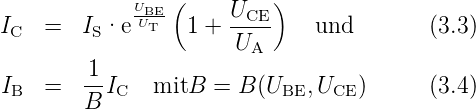
IS ≈ 10−16 −10−12A ist der Sättigungssperrstrom, UT ≈ 26mV die Temperaturspannung bei Raumtemperatur, UA die im Ausgangskennlinienfeld (IC(UCE)) extrapolierte Early–Spannung und B die Stromverstärkung. Je grösser UA bzw. je flacher die Ausgangskennlinien, desto übersichtlicher sind die Kennlinienfelder.
Die praktische Verwendung wird häufig bestimmt durch die
Nichtlinearität/Stromabhängigkeit der Stromverstärkung B
bzw. der differentiellen Stromverstärkung β = 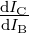 , siehe Bild
3.97. Ebenso ist der Eingangswiderstand stromabhängig. Im
sog. Grosssignalbetrieb wird das Transistorverhalten sehr
komplex; insbesondere das dynamische Verhalten. (Bei
hohen Strömen verändern sich die Schaltgeschwindigkeit,
die Grenzfrequenz sinkt.) Stets erfordern die möglichen
Durchbruchserscheinungen die strikte Beachtung der
ausgewiesenen Grenzwerte (maximale Sperrspannung,
maximale Emitterspannung, maximale Ströme, maximale
Verlustleistung). Die Folgen möglicher Temperaturdrift
müssen meist beim Schaltungsdesign berücksichtigt werden.
, siehe Bild
3.97. Ebenso ist der Eingangswiderstand stromabhängig. Im
sog. Grosssignalbetrieb wird das Transistorverhalten sehr
komplex; insbesondere das dynamische Verhalten. (Bei
hohen Strömen verändern sich die Schaltgeschwindigkeit,
die Grenzfrequenz sinkt.) Stets erfordern die möglichen
Durchbruchserscheinungen die strikte Beachtung der
ausgewiesenen Grenzwerte (maximale Sperrspannung,
maximale Emitterspannung, maximale Ströme, maximale
Verlustleistung). Die Folgen möglicher Temperaturdrift
müssen meist beim Schaltungsdesign berücksichtigt werden.
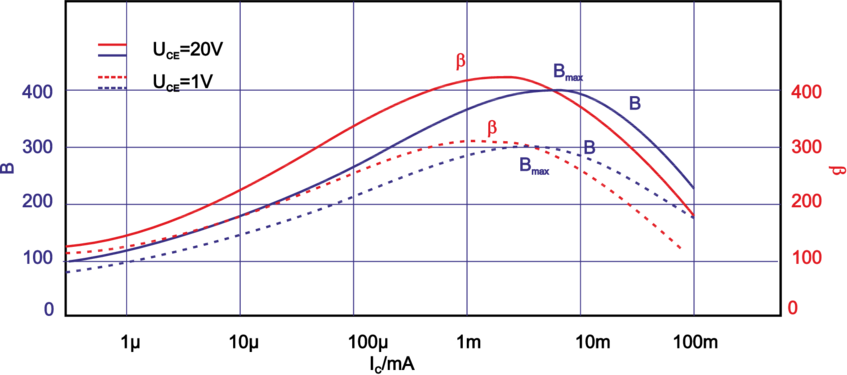
| Abbildung 3.97.: | Gross– und Kleinsignalverstärkung B und β eines Kleinleistungstransistors im Normalbetrieb (skizziert nach Tietze/Schenk [TS99]). |
Eine wichtige Anwendung des Transistors ist die lineare Verstärkung von Signalen im sog. Kleinsignalbetrieb. Hierzu wird der Transistor — durch äussere Beschaltung — in einem Arbeitspunkt festgehalten und mit kleinen Signalen um den Arbeitspunkt ausgesteuert. Der ausgesteuerte Kennlinienabschnitt wird näherungsweise beschrieben durch die Tangente im Arbeitspunkt; je besser die Übereinstimmung von Kurve und Tangente im Aussteuerbereich, desto besser ist das ‘lineare Verhalten’.
Der Arbeitspunkt A wird durch die Spannungen UCE,A und UBE,A und die Ströme IC,A und IB,A bestimmt. Die Bestimmung des Arbeitspunktes bei bekannter Beschaltung soll anhand des Beispiels in Abbildung 3.98 kurz aufgerissen werden.
Der Transistor wird im Maximum der Kleinsignalstromverstärkung
betrieben, keinesfalls aber bei grösseren Strömen; den
entsprechenden Wert findet man im Datenblatt: IC,A.
Vernünftigerweise gelte immer UCE,A > UCE,sat. Man
berechnet IB,A und zeichnet im Eingangskennlinienfeld die
Lastgerade I1 = 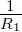 (UB1 −UBE) ein: Da die Kennlinie nur
schwach von UCE abhängt, ist IB,A eindeutig festlegbar
und die Lastgerade von UB1 durch IB,A legbar. Der
Schnittpunkt mit der Stromachse liefert den Wert für R1. Im
Ausgangskennlinienfeld ist die Vorgehensweise analog: UB2 ist
vorgegeben, UCE,A wird gewählt, so dass die mit UBE,A
festgelegte Kennlinien im Schnittpunkt wieder IC,A liefert und
die Extrapolation auf UB2∕R2, also auf R2 erlaubt. Dieser
graphischen Bestimmung des Arbeitspunktes ist die Lösung
des Gleichungssystems aus den beiden Kennliniengleichungen
des Transistors und den beiden Lastgeradengleichungen
äquivalent.
(UB1 −UBE) ein: Da die Kennlinie nur
schwach von UCE abhängt, ist IB,A eindeutig festlegbar
und die Lastgerade von UB1 durch IB,A legbar. Der
Schnittpunkt mit der Stromachse liefert den Wert für R1. Im
Ausgangskennlinienfeld ist die Vorgehensweise analog: UB2 ist
vorgegeben, UCE,A wird gewählt, so dass die mit UBE,A
festgelegte Kennlinien im Schnittpunkt wieder IC,A liefert und
die Extrapolation auf UB2∕R2, also auf R2 erlaubt. Dieser
graphischen Bestimmung des Arbeitspunktes ist die Lösung
des Gleichungssystems aus den beiden Kennliniengleichungen
des Transistors und den beiden Lastgeradengleichungen
äquivalent.
Im Kleinsignalbetrieb werden die Abweichungen von den Arbeitspunktwerten als Kleinsignalspannungen uBE und uCE bzw. als Kleinsignalströme iB und iC bezeichnet. Die Verknüpfung zwischen den Strömen und den Spannungen liefern die sog. Kleinsignalgleichungen. Man kann sie auch in Matrizen–Form wiedergeben:
![[ ] [ ] [ ][ ]
iB uBE Y11,e Y12,e uBE
= Ye = .
iC uCE Y21,e Y22,e uCE](phys_elektr685x.png) | (3.5) |
Diese Darstellung ist äquivalent der Leitwert–Darstellung eines Vierpols. Der Index e der Y –2 x 2–Matrix steht für Emitterschaltung. Die Matrixkomponenten werden durch die sog. Kleinsignalparameter festgelegt, die alle aus den Kennlinienfeldern als Steigung der Tangente in den Arbeitspunkten ermittelt werden können:

Den Kleinsignalgleichungen entspricht (mit der Näherung Sr = 0) ein Ersatzschaltbild, das sog. Kleinsignalersatzschaltbild des Bipolartransistors. Neben dem Eingangs– und Ausgangswiderstand bestimmt die Stromquelle S·uBE das Niederfrequenzverhalten des Transistors.
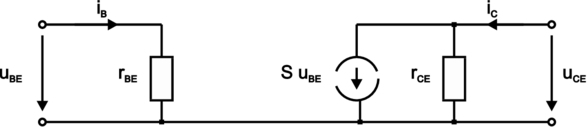
| Abbildung 3.100.: | Gleichstrom–Kleinsignalersatzschaltbild des Bipolartransistors (skizziert nach Tietze/Schenk [TS99]). |
Neben dieser Leitwertdarstellung gibt es noch eine zweite, übliche Variante: die Hybriddarstellung mit der H–Matrix:
![[ ] [ ]
uBE iB
i = He u .
C CE](phys_elektr687x.png) | (3.10) |
Beide Darstellungen sind ineinander überführbar. Mit Hilfe dieser Vierpoldarstellungen können Transistorschaltungen unter Benutzung der Matrizenarithmetik berechnet werden. Die Vierpolparameter sind allerdings vom gewählten Arbeitspunkt und der Frequenz abhängig. Ihre konkrete Formulierung hängt jeweils von den gewählten Grundgleichungen und den daraus abgeleiteten Modellen ab. Sie sind Grundlage von Schaltungssimulationsprogrammen wie — siehe Praktikum — PSPICE (Firma MicroSim).
Bekannte Modelle, die das statische Verhalten eines Bipolartransistors beschreiben, sind das Ebers–Moll–Modell, das Transportmodell und das Gummel–Poon–Modell. Letzteres ist das vollständige, nichtlineare Modell aus dem durch Linearisierung am Arbeitspunkt statische und dynamische Kleinsignalmodelle abgeleitet werden.
Dem Buch von P. Horrowitz/W. Hill folgend, kann man mit Hilfe zweier einfacher Modelle bereits ein elementares Verständnis für viele Transistor–Grundschaltungen entwickeln, ohne zum H–Parameter–Modell oder diversen Ersatzschaltungen greifen zu müssen.
Das einfachste Transistormodell ist das des ‘Stromverstärkers’. Es lautet:
Im Stromverstärker–Modell bestimmt IB also den Wert von IC, man gibt den Basisstrom vor. Die letzte Aussage bedeutet auch, dass ein kleiner (Basis–) Strom einen einhundert mal grösseren zum Kollektor hin steuert. Leider ist die Stromverstärkung B keine feste und stabile Grösse. Eine Schaltung sollte nie ein bestimmtes, konstantes B voraussetzen.
Das verbesserte Modell nennt sich ‘Transkonduktanzverstärker’–Modell. In diesem wird die vierte Modellannahme des Stromverstärker–Modells verbessert: IC wird jetzt von UBE∕UT und IS(T) bestimmt:
![[ UBE ] UBE
IC = IS eUT − 1 ≈ Is·e UT , ‘Ebers–Modell –Gleichung ’.](phys_elektr688x.png) | (3.11) |
Man gibt statt des Stromes IB jetzt die Spannung UBE
in der Schaltung vor. In der Praxis führt das aber
wegen des hohen negativen Temperaturkoeffizienten der
Basis–Emitter-Spannung (IS(T), -2,1 mV/K) nicht direkt zu
erfolgreichen Schaltungsentwürfen. Temperaturstabile
Schaltungen erhält man erst durch Spannungs– oder
Stromgegenkopplung, siehe später.
Nebenbemerkung: Man nennt das ‘Transkonduktanzverstärker’–Modell
in der obigen Form auch ‘Reduziertes Ebers–Moll–Modell für
den Bipolartransistor–Normalbetrieb’.
Grundschaltungen mit einem Bipolartransistor sind die Emitterschaltung (common emitter configuration), die Kollektorschaltung (common collector configuration) und die Basisschaltung (common base configuration). Den Namen der Schaltung bestimmt der Transistoranschluss, der als gemeinsamer Bezugsknoten für den Eingang und den Ausgang der Schaltung dient. (Schwächeres Kriterium).
Die Emitterschaltung (ohne Gegenkopplung) ist in Abbildung 3.101 gezeigt. Eine Spannungsquelle Ug mit dem Innenwiderstand Rg liefert die Eingangsspannung UE. Der Emitteranschluss liegt — kennzeichnend für diese Schaltung — direkt an Masse, der Kollektor über den Kollektorwiderstand RC (typ. 1kΩ) an der Versorgungs–Spannungsquelle UB (typ. 5 V).
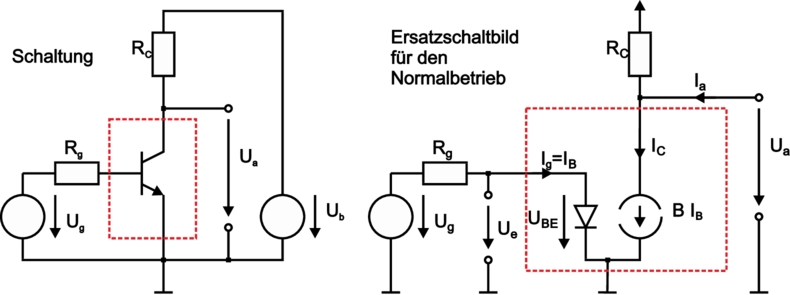
| Abbildung 3.101.: | Emitterschaltung: Schaltbild und Ersatzschaltbild für den Normalbetrieb (skizziert nach Tietze/Schenk [TS99]). |
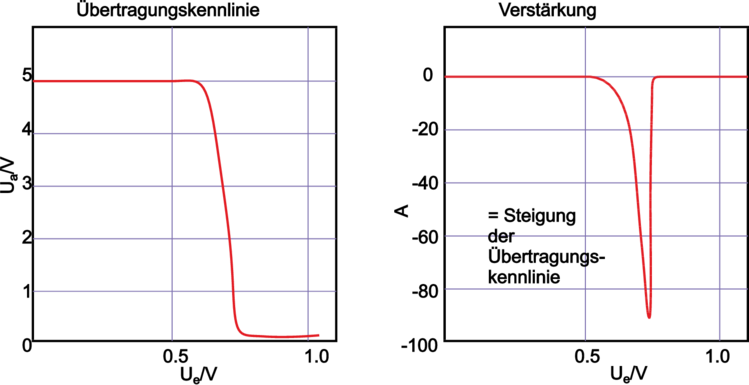
| Abbildung 3.103.: | Emitterschaltung: Übertragungskennlinie und Verstärkung (skizziert nach Tietze/Schenk [TS99]). |
Die gemessene Übertragungskennlinie UA(Ug) ist in Abbildung 3.102 oben gezeigt. Für 0, 5V ≤Ug ≤ 0, 7V nimmt Ua = Ub −IC·RC ab; in diesem Bereich des Normalbetriebs liegt der Arbeitspunkt (o).
Das oben ebenfalls gezeigte Ersatzschaltbild für diesen Kennlinienbereich ist das sog. vereinfachte Transportmodell; dabei ist der Early–Effekt vernachlässigt und es gilt B = β = konst. Man erhält:
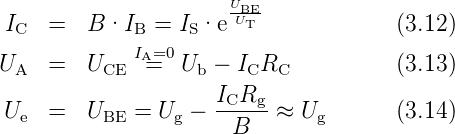
Typische Zahlenwerte am gewählten Arbeitspunkt sind mit B = …100 und IS = …fA: IC ≈ mA, IB ≈…μA, Ue < 1V und Ug < 1V.
Einen Hinweis auf das Kleinsignalverhalten erhält man aus der Kleinsignal–Spannungsverstärkung A; sie entspricht der Steigung der Übertragungskennlinie. Sie ist sehr stark vom Arbeitspunkt abhängig, d. h. dieser muss genau und temperaturstabil eingestellt werden. Schon bei kleinsten Aussteuerungen erhält man eine nichtlineare Verzerrung des Signals.

| Abbildung 3.104.: | Emitterschaltung: Kleinsignal–Ersatzschaltbild (skizziert nach Tietze/Schenk [TS99]). |
Aus dem Kleinsignal–Ersatzschaltbild erhält man (ohne Lastwiderstand RL):
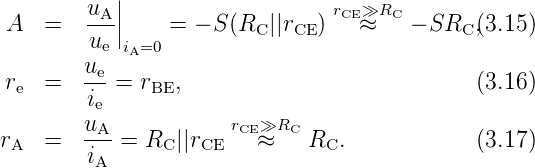
Grösster Schwachpunkt der Emitterschaltung ist aber die Temperaturinstabilität. Wird die Temperatur um 1 Grad erhöht, muss man die Eingangsspannung um 2 mV erniedrigen, um den Kollektorstrom konstant zu halten. Andernfalls driftet die Ausgangsspannung um ca. A·2mV. Eine Temperaturdrift verschiebt also den Arbeitspunkt und damit die Verstärkung etc. Praxistaugliche Schaltungen erhält man durch Gegenkopplung.
Die Emitterschaltung mit Stromgegenkopplung:
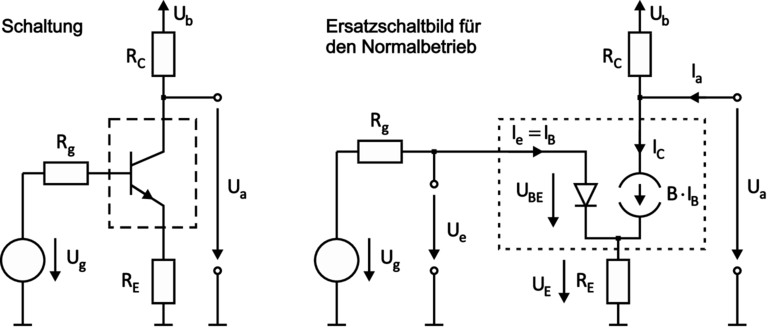
| Abbildung 3.105.: | Emitterschaltung mit Stromgegenkopplung: Schaltung und Ersatzschaltbild (Normalbetrieb) (skizziert nach Tietze/Schenk [TS99]). |
Durch Einfügen eines Emitterwiderstand RE (typ. 500Ω) wird die Übertragungskennlinie deutlich verändert, siehe Bild unten. Der Arbeitsbereich beträgt jetzt ein gutes Volt und die Kennlinie verläuft annähernd linear; der Arbeitspunkt wird mittig gewählt. Die Kleinsignal–Verstärkung spiegelt dies in einem annähernd konstanten Mittelteil wieder. Allerdings erkauft man sich diesen Stabilitätsgewinn durch einen Verlust an Verstärkung. Dies zwingt einen zum Bau mehrstufiger Verstärker.
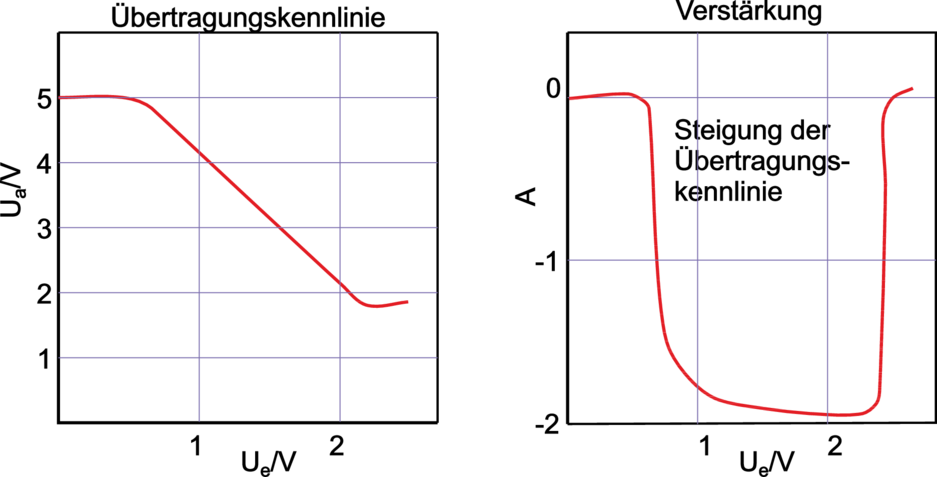
| Abbildung 3.106.: | Emitterschaltung mit Stromgegenkopplung: Übertragungskennlinie und Verstärkung (gezeichnet nach Tietze/Schenk [TS99]). |
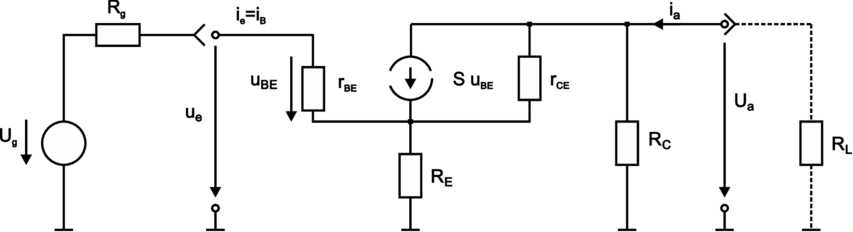
| Abbildung 3.107.: | Emitterschaltung mit Stromgegenkopplung: Kleinsignal–Ersatzschaltbild (skizziert nach Tietze/Schenk [TS99]). |
Aus dem Ersatzschaltbild erhält man näherungsweise für rCE »RC,RE und β » 1, sowie RL = 0:
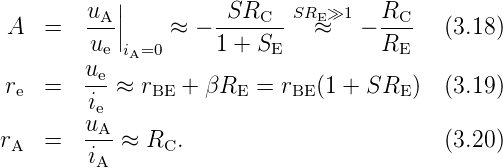
Die Verstärkung wird in erster Näherung nicht vom Transistor, sondern von den äusseren Beschaltungswiderständen festgelegt. RE sorgt für Stabilität und Linearität, erhöht den Eingangswiderstand (!), belässt den Ausgangswiderstand unverändert, aber senkt die Verstärkung stark ab und darf deshalb auch nicht zu gross gewählt werden. Das Verstärkungs–Bandbreite–Produkt bleibt im übrigen fast unverändert.
Die Emitterschaltung mit Spannungsgegenkopplung: Hier fügt man zwischen Basis– und Kollektoranschluss einen Widerstand ein (typisch R1 = RC = 1kΩ, R2 = 2kΩ), wodurch ein Teil der Ausgangsspannung auf den Eingang zurückgekoppelt wird. Nochmals ist der Arbeitsbereich vergrössert, die Verstärkung ist von vergleichbarer Qualität und annähernd symmetrisch um Ue = 0.
Aus dem Ersatzschaltbild erhält man näherungsweise:
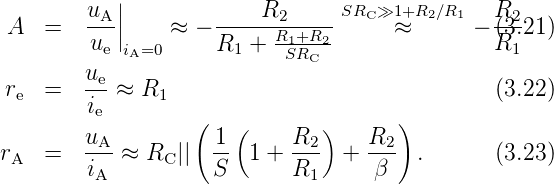
Die Verstärkung wird durch R2∕R1 bestimmt, also wieder durch die Gegenkopplung. Der Eingangswiderstand ist relativ klein, der Ausgangswiderstand der niedrigste im Vergleich; dies ist bei niederohmigen oder kapazitiven Lasten von Vorteil.
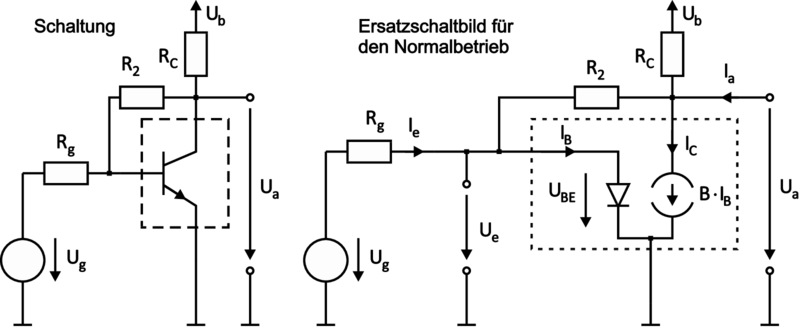
| Abbildung 3.108.: | Emitterschaltung mit Spannungsgegenkopplung: Schaltung und Ersatzschaltbild (Normalbetrieb) (skizziert nach Tietze/Schenk [TS99]). |
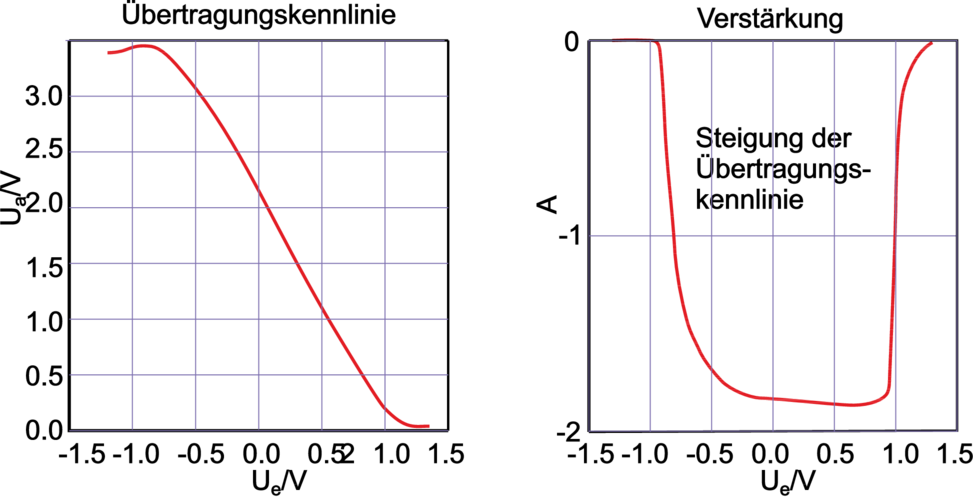
| Abbildung 3.109.: | Emitterschaltung mit Spannungsgegenkopplung: Übertragungskennlinie und Verstärkung (skizziert nach Tietze/Schenk [TS99]). |

| Abbildung 3.110.: | Emitterschaltung mit Spannungsgegenkopplung: Kleinsignal–Ersatzschaltbild (skizziert nach Tietze/Schenk [TS99]). |
Wählt man R1 = 0 und gibt einen Ansteuerstrom Ie vor, so erhält man einen Strom–Spannungs–Wandler (Transimpedanzverstärker). Über einen typischen Bereich von etwa einem mA arbeitet dieser Verstärker mit guter Linearität.
Zur Arbeitspunkteinstellung ist ganz allgemein festzustellen, dass der Arbeitspunkt möglichst wenig von den — streuenden — Transistorparametern abhängen sollte. Es gibt zwei prinzipiell unterschiedliche Verfahren, nämlich die Gleichspannungs–Kopplung und die Wechselspannungs–Kopplung. Im letzteren Fall werden Ein– und Ausgang des Verstärkers über Koppelkondensatoren mit dem Signal bzw. der Last verbunden.
Die Kollektorschaltung — siehe Bild 3.111 — besteht aus dem Transistor mit RE und UB (typisch 1kΩ und +5V), der Signalspannungsquelle Ug mit ihrem Innenwiderstand Rg.
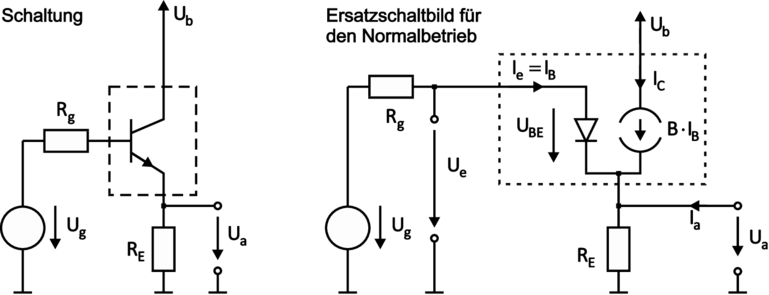
| Abbildung 3.111.: | Kollektorschaltung: Schaltbild und Ersatzschaltbild für den Normalbetrieb (skizziert nach Tietze/Schenk [TS99]). |
Aus dem Ersatzschaltbild und dem vereinfachten Transportmodell folgt:
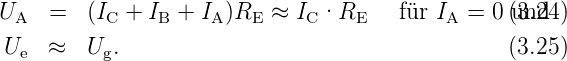
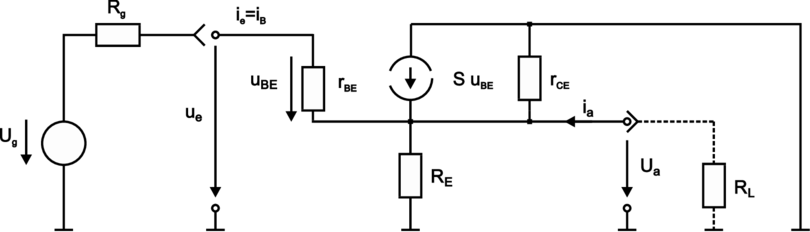
| Abbildung 3.113.: | Kollektorschaltung: Kleinsignal–Ersatzschaltbild (skizziert nach Tietze/Schenk [TS99]). |
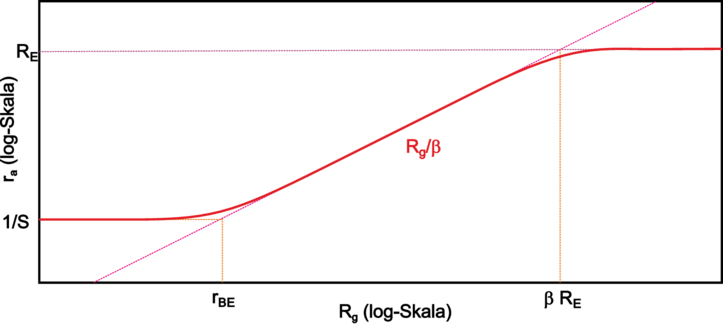
| Abbildung 3.114.: | Kollektorschaltung: Widerstandstransformation rA(Rg) (skizziert nach Tietze/Schenk [TS99]). |
Das Kleinsignalverhalten entnimmt man wieder dem zugehörigen Ersatzschaltbild. Will man zusätzlich den Einfluss eines Lastwiderstandes RL berücksichtigen, muss man statt RE die Parallelschaltung von RE und RL berücksichtigen. Man erhält:
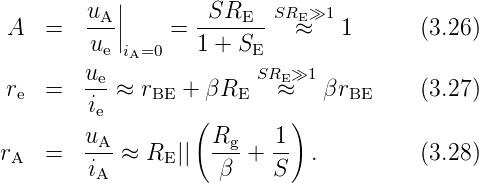
Die Basisschaltung schliesslich ist im nächsten Bild gezeigt. Die Basis liegt auf konstantem Potential, der Widerstand RBV (z. B. 1kΩ) begrenzt den Basisstrom bei Übersteuerung und spielt im Normalbetrieb keine Rolle. Das Eingangssignal wird direkt an den Emitter gekoppelt. Kapazitives Übersprechen ist hierdurch minimiert, höchste Frequenzen werden noch verstärkt. Die Basischaltung wird deshalb gern in Hochfrequenzschaltungen eingesetzt. Weitere Werte RC ≈ 1kΩ, UB = +5V typ.
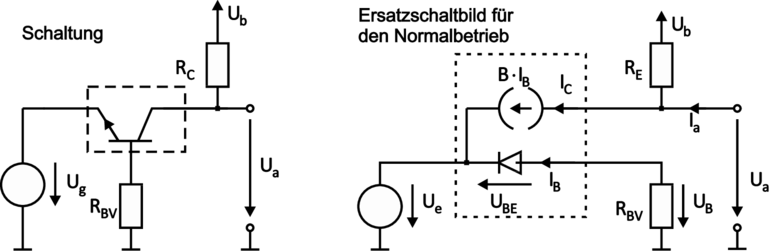
| Abbildung 3.115.: | Basisschaltung: Schaltbild und Ersatzschaltbild für den Normalbetrieb (skizziert nach Tietze/Schenk [TS99]). |
Aus dem Ersatzschaltbild und dem vereinfachten Transportmodell erhält man:

Der Arbeitspunkt wird mittig in den abfallenden Bereich der Übertragungskennlinie gelegt. Man erhält näherungsweise und mit RL = 0:
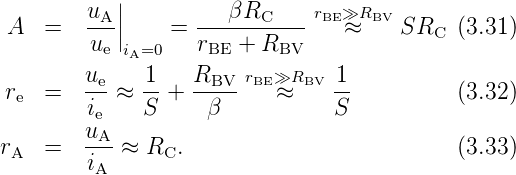
Die Eingangsimpedanz ist also vergleichsweise niedrig und passt damit sehr gut an planare Wellenleiter (siehe integrierte Optoelektronik).

| Abbildung 3.117.: | Basisschaltung: Kleinsignal–Ersatzschaltbild (skizziert nach Tietze/Schenk [TS99]). |
Steuert man die Basisschaltung mit einer Stromquelle an, so
tritt anstelle der Verstärkung A der Übertragungswiderstand
RT, die sog. Transimpedanz RT = 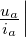 iA=0 ≈ RC. Der
Klirrfaktor des Strom–Spannungs–Wandlers in der
Basisschaltung ist besonders klein.
iA=0 ≈ RC. Der
Klirrfaktor des Strom–Spannungs–Wandlers in der
Basisschaltung ist besonders klein.
Reicht die Stromverstärkung eines einzelnen Transistors nicht aus, so greift man zur Darlington–Schaltung:
Der Emitterstrom des Eingangstransistors fliesst in die Basis des zweiten Transistors. In erster Näherung gilt für die Stromverstärkung:
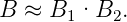 | (3.34) |
Darlington–Transistoren kann man wie Einzeltransistoren (in einem Gehäuse) kaufen. Sie werden häufig als Schalter eingesetzt: Aufgrund der grossen Verstärkung können grosse Ströme geschaltet werden. Allerdings schaltet der 2. Transistor und damit der gesamte Darlington–Transistor langsam. Die in der Basis gespeicherte Ladung leitet man deshalb über den Widerstand R ab; der Darlington–Transistor kann so schneller gesperrt werden, allerdings auf Kosten der Stromverstärkung.
Schaltungen, die Feldeffekttransistoren enthalten, verwirren viele. Zu unrecht, denn die Unterschiede zu den Bipolartransistoren sind im Grundsatz sekundär. Den Bipolartransistor–Anschlüssen Emitter (E), Basis (B), Kollektor (K) und Substrat (S) entsprechen die Feldeffekttransistor–Anschlüsse Source (S), Gate (G), Drain (D) und Bulk (B). Ersetzt man im vorigen Kapitel in den Gleichungen bei den Strömen und Spannungen die korrespondierenden Anschlussbezeichungen, erhält man erstaunlich häufig die gültigen Bezeichnungen für die Grundschaltungen mit Feldeffekttransistoren und in nullter Näherung zeigen die entsprechenden Kennlinien den selben Verlauf. Auch die Grenzwerte ähneln einander stark.
Es gibt eine ganze Reihe von Feldeffekttransistoren: 4 Typen von MOSFETs, 2 Typen von JFETs und 2 von MESFETs. Zur Übersicht trägt aber bei, dass die Ausgangskennlinien aller Bauelemente mit n–Kanal sich ähneln (positive JD für positive UDS) und die für alle p–Kanal–Bauelemente ebenfalls (negative ID für negative UDS). Auch die Übertragungskennlinien der n–Kanal (bzw. gespiegelt am Ursprung die der p–Kanal–Bauelemente) zeigen einen Dioden–ähnlichen Verlauf; die der einzelnen Typen sind lediglich auf der UGS–Achse gegeneinander verschoben. (Die zugehörigen Schwellspannungen UGS,th können positive und negative Werte annehmen.)
Das statische Verhalten eines FETs beschreiben wieder seine Kennlinien. Die Eingangskennlinien zeigen im normalen Arbeitsbereich nur Nulllinien: der Gatestrom ist vernachlässigbar klein, die Steuerung mit UGS erfolgt leistungslos. Dies ist ein wesentlicher Unterschied zu den Bipolartransistoren, d. h. das entsprechende ‘rBE’ ist ∞.
Eine empirische Beschreibung der Kennlinien geben die sog. Grosssignalgleichungen (näherungsweise) wieder.
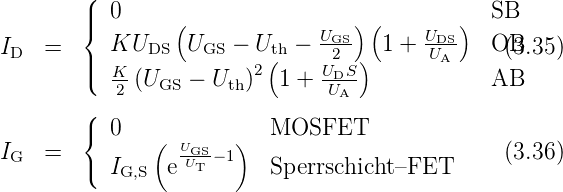
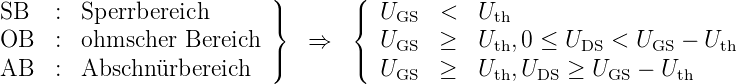
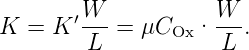 | (3.37) |
Der Anstieg im annähernd linearen ohmschen Kennlinienbereich
ist mit der Beweglichkeit der Ladungsträger im Kanal, dem
Kapazitätsbelag des Gate–Oxids und der Geometrie des Gates
verbunden. Diese Gleichungen gelten für die vergleichsweise
gross dimensionierten Einzel–FETs, wobei Drain und Source
i. allg. nicht vertauscht werden dürfen (unsymmerische
Bauelemente). Bei den immer kleiner dimensionierten
integrierten FETs wird die Beschreibung zunehmend
schwieriger und die zugehörigen Modelle, insbesondere zur
Beschreibung der dynamischen Eigenschaften, wie sie in
Schaltungssimulationen benötigt werden, werden immer
umfangreicher. Im Grundsatz gilt aber, dass K ∼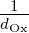 ·
·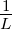 ist,
d. h. die Miniaturisierung die Steilheit vergrössert.
ist,
d. h. die Miniaturisierung die Steilheit vergrössert.
Im ohmschen Bereich kann der FET als steuerbarer Widerstand betrieben werden. In der Umgebung von UDS = 0 wirkt der FET bei Aussteuerung mit kleinen Amplituden als steuerbarer linearer Widerstand, bei grösseren Amplituden zunehmend nichtlinear, ebenso für UDS > 0. Mögliche linearisierte Schaltungen vermeiden letzteres auf Kosten der Grösse des Abstimmbereichs.
Obwohl das Grosssignalverhalten des FETs deutlich besser ist als das der Bipolartransistoren, ist eine wichtige FET–Anwendung die lineare Verstärkung von Signalen im Kleinsignalbetrieb. Der Arbeitspunkt liegt im Abschnürbereich. Das früher zu Kleinsignalgrössen und –Gleichungen gesagte gilt analog. Besonders einfach werden die Verhältnisse wieder beim Einzel–FET, bei dem Source und Bulk miteinander verbunden sind und die Source–Bulk–Diode wegen USB = 0 im Kleinsignalersatzschaltbild nicht berücksichtigt werden muss (Die Stromquelle mit der Substrat–Steilheit SB und die Bulk–Source–Kapazität entfallen.).
Die Unterschiede vom FET–Verhalten gegenüber dem der
Bipolartransistoren kann man zusammenfassen:
FETs sind extrem ladungsempfindlich und erfordern
besondere Schutzmassnahmen. Sie besitzen einen negativen
Temperaturkoeffizient (JFETs) bzw. werden meist im Bereich
mit negativen Temperaturkoeffizient betrieben (MOSFET);
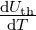 liegt bei rund −2
liegt bei rund −2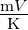 und sie benötigen keinen
zusätzlichen Stabilisierungsaufwand. Das Grosssignalverhalten
ist günstiger. Bei gleichen Aussteueramplituden sind
FET–Kleinsignalverstärker klirrärmer, bei hochohmigen
Quellen sind FETs deutlich rauschärmer (Anwendung:
Photodioden–Vorverstärker); JFETs zeigen dabei das geringere
1∕f–Rauschen (kleine Frequenzen!). Bei niederohmigen
Quellen dagegen hat der Bipolartransistor das deutlich
bessere Rauschverhalten.
und sie benötigen keinen
zusätzlichen Stabilisierungsaufwand. Das Grosssignalverhalten
ist günstiger. Bei gleichen Aussteueramplituden sind
FET–Kleinsignalverstärker klirrärmer, bei hochohmigen
Quellen sind FETs deutlich rauschärmer (Anwendung:
Photodioden–Vorverstärker); JFETs zeigen dabei das geringere
1∕f–Rauschen (kleine Frequenzen!). Bei niederohmigen
Quellen dagegen hat der Bipolartransistor das deutlich
bessere Rauschverhalten.
Grundschaltungen mit einem FET sind die Source–Schaltung (common source configuration), die Drain–Schaltung (common drain configuration) und die Gate–Schaltung (common gate configuration). Der gemeinsame Bezugspunkt für Schaltungsein– und –Ausgang gibt wieder den Namen. (Schwächeres Kriterium)
Die Sourceschaltung entspricht der Emitterschaltung, siehe Abbildungen. Wegen des grösseren Steilheitskoeffizienten (höhere Ladungsträgerbeweglichkeit) werden meist n–Kanal–MOSFETs bevorzugt, selbstsperrende MOSFETs häufiger als selbstleitende.
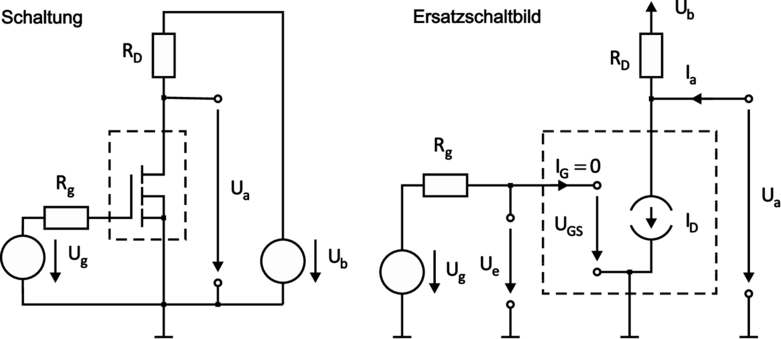
| Abbildung 3.121.: | Sourceschaltung: Schaltung und Ersatzschaltbild (skizziert nach Tietze/Schenk [TS99]). |
Der MOSFET hat einen extrem hohen Eingangswiderstand, IG = 0 und die BE–Diode der korrespondierenden Emitterschaltung entfällt hier. Der Innenwiderstand Rg der Quelle hat keinen Einfluss auf die Kennlinie, wohl aber auf das dynamische Verhalten.
Das Kleinsignalverhalten der FETs ist gekennzeichnet durch die geringere Verstärkung bei vergleichbaren Strömen bzw. Arbeitspunkten aufgrund ihrer geringeren Steilheit im Vergleich zu Bipolartransistoren. Die korrespondierenden Kleinsignalersatzschaltbilder unterscheiden sich nur in re = ∞ (gegenüber re = rBE), ebenso die Ausdrücke für die Spannungsverstärkung A, sowie die Ein– und Ausgangswiderstände re und rA.
Aufgrund der günstigeren Klirrfaktoren wird die Sourceschaltung gerne in schmalbandigen HF–Verstärkern eingesetzt.
Die vorhandene Nichtlinearität und Temperaturabhängigkeit kann wieder durch Einfügen eines Widerstands RS verbessert werden: Sourceschaltung mit Stromgegenkopplung. Auch hier gilt, bis auf re = ∞ die Analogie zur Emitterschaltung mit Stromgegenkopplung.
Ähnliches gilt für die Sourceschaltung mit Spannungsgegenkopplung. Schaltung, Kennlinie und Kleinsignalersatzschaltbild entsprechen ganz, die Kleinsignal–Formeln sind modifiziert. Diese Schaltung wird sehr selten eingesetzt, da der hohe FET–Eingangswiderstand nicht genutzt wird. Entfernt man aber den eingangsseitigen Widerstand, so erhält man eine Strom–Spannungs–Wandler–Schaltung (Transimpedanzverstärker). Diese rauscharme Schaltung wird gerne bei Photodioden–Empfängern eingesetzt; die Diode wird im Sperrbereich betrieben und wirkt als Stromquelle mit hohem Innenwiderstand.
entspricht der Kollektorschaltung. Analog wird sie auch Sourcefolger genannt. Sie ist hervorragend geeignet, hochohmige Quellen zu puffern. Die Eingangskapazität ist extrem klein. Da der Ausgangswiderstand > 50Ω ist, benützt man gerne eine Darlingtonschaltung aus FET und Bipolarverstärker mit kleinerem rA und höheren Ausgangsströmen.
Bei der Gateschaltung schliesslich
gilt wieder viel Analoges zur Basisschaltung einschliesslich des Kleinsignalverhaltens. Hervorzuheben ist hier die sehr übersichtliche Verwendung als Strom–Spannungs–Wandler mit einem rA ≈RD.
Eine Stromquelle (current source) liefert an einem Verbraucher RL einen konstanten Strom: Konstantstromquelle; idealerweise unabhängig vom momentanen Spannungsabfall an RL. Stromquellen sind spannungsgesteuert, d. h. eine kleine Steuerspannung bestimmt das Verhalten einer Schaltung mit grossem Ausgangswiderstand. Eingesetzt werden sie z. B. zur Einstellung von Arbeitspunkten, als wesentliche Bestandteile diverser Generatoren oder zur Versorgung von elektrochemischen Zellen und optoelektronischen Bauelementen (LEDs, Laserdioden) etc.
Das Prinzip einer einfachen Stromquelle beruht auf der Emitterschaltung bzw. (bei diskreten Schaltungen selten) auf der Source–Schaltung, siehe Abbildung 3.124; zur Stabilisierung meist mit Stromgegenkopplung. Dabei wird die Basis (bzw. das Gate) auf möglichst konstantem Potential gehalten. Verwendet man Transistoren (im Normalbetrieb) mit grosser Early–Spannung, dann ist im ‘Arbeitsbereich’ der Ausgangsstrom durch RL praktisch konstant.
Einige einfache Stromquellen für diskrete Schaltungen zeigt Abbildung 3.125. Von links geschieht die Festlegung der konstanten Basisspannung durch a) einen Spannungsteiler, b) einen Spannungsteiler mit Diode zur Kompensation der Temperaturabhängigkeit von UBE des Transistors und c) mit Zenerdiode (mit der geringen Temperaturabhängigkeit des Zenerdurchbruchs).
Ein Stromspiegel (current mirror) ist eine stromgesteuerte Stromquelle, d. h. am Ausgang erhält man eine verstärkte oder identische oder abgeschwächte Kopie des Eingangsstroms. Bei konstantem Eingangsstrom funktioniert jeder Stromspiegel als Konstant–Stromquelle.
Der einfache Stromspiegel besteht aus zwei Transistoren (genauer aus npn–Diode und npn–Transistor bzw. aus n–Kanal–Diode und n–Kanal–MOSFET) und — optional — aus zwei Widerständen zur Stromgegenkopplung. Mit einem zusätzlichen, hinreichend grossen Vorwiderstand RV kann man den Eingangsstrom als konstanten Refererenzstrom festlegen; man erhält so eine Konstant–Stromquelle.
Das sog. Übersetzungsverhältnis Ki = 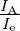 hängt beim
npn–Stromspiegel ohne Gegenkopplung (möglich bei
integrierten Schaltungen) vom Verhältnis
hängt beim
npn–Stromspiegel ohne Gegenkopplung (möglich bei
integrierten Schaltungen) vom Verhältnis 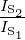 ab, also
vom Grössenverhältnis der Transistoren. In diskreten
Schaltungen ist nur der npn–Stromspiegel mit Gegenkopplung
realisierbar; hier gilt Ki ≈
ab, also
vom Grössenverhältnis der Transistoren. In diskreten
Schaltungen ist nur der npn–Stromspiegel mit Gegenkopplung
realisierbar; hier gilt Ki ≈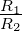 . Ohne Gegenkopplung ist bei
konstantem Übersetzungsverhältnis (z. B. Ki = 1) die
Übertragungskennlinie IA(Ie) über mehrere Dekaden linear,
mit Gegenkopplung etwas kleiner.
. Ohne Gegenkopplung ist bei
konstantem Übersetzungsverhältnis (z. B. Ki = 1) die
Übertragungskennlinie IA(Ie) über mehrere Dekaden linear,
mit Gegenkopplung etwas kleiner.
Nebenbemerkung: Der Arbeitsbereich von npn–Stromspiegeln ist immer grösser als der vergleichbarer n–Kanal–Stromspiegel.
Das limitierte Verstärkungs–Bandbreite–Produkt der Emitterschaltung begrenzt auch den einfachen Stromspiegel. Man greift deshalb gerne zur Kaskodenschaltung, meistens um eine grössere Verstärkung zu erreichen. Sie ist u. a. in vielen OP– und HF–Verstärkern enthalten.
Bei der Kaskodenschaltung werden eine Emitter– und eine Basisschaltung (bzw. eine Source– und eine Gateschaltung) in Reihe gesetzt, wodurch der Miller–Effekt der Emitter–Schaltung vermieden wird. Von den Lastschwankungen an RC sieht der Transistor T1 praktisch nichts, sein UCE bleibt unverändert und damit bleibt auch der Strom durch die Kaskode und durch RV konstant.
Ersetzt man in der Prinzipschaltung den Emitterwiderstand RE durch einen einfachen Stromspiegel, erhält man den ‘Stromspiegel mit Kaskode’, einen Stromspiegel mit 3 Transistoren. Sein Hauptvorteil ist der erhöhte Ausgangswiderstand. Eine weitere Vergrösserung des Aussteuerbereichs erfordert komplexere Kaskoden–Stromspiegel mit 4, 5, 6 Transistoren plus Transistoren zur Arbeitspunkteinstellung.
Eine äusserst wichtige Grundschaltung in der integrierten Schaltungstechnik ist der Differenzverstärker (differential amplifier, long tailed pair); er bildet die Basis für den Operations–Verstärker.
Seine Grundschaltung ist symmetrisch aufgebaut mit zwei Eingängen und zwei Ausgängen. Zwei Emitterschaltungen (bzw. Source–Schaltungen) sind so angeordnet, dass die Emitter (bzw. Sources) gemeinsam mit einer Stromquelle verbunden sind, siehe Abbildung 3.128. Die Versorgungsspannung ist meist symmetrisch positiv und negativ: ±UB.
Bei symmetrischem Aufbau fliesst durch jeden Transistor genau der halbe Strom. Erhöht die Spannung an einem Eingang den Strom durch den Transistor, so muss — wegen der Konstantstromquelle — der Strom am anderen Transistor entsprechend sinken. Die Spannungsänderungen an den ‘Lastwiderständen’ RC1 und RC2 sind also gegensinnig.
Legt man gleichsinnige Signale an die beiden Eingänge gleichzeitig an, so ändern sich zwar die Transistorwiderstände, aber die Konstantstromquelle hält die Ströme konstant und damit bleiben die Spannungsabfälle an RC1, RC2, also an den Ausgängen konstant. Die sog. Gleichtaktverstärkung (common mode gain) ist im Idealfall gleich Null; solange der Gleichspannungsanteil hinreichend klein ist, kann jede Signalquelle direkt an den Differenzverstärker angeschlossen werden.
Legt man dagegen eine schiefsymmetrische Differenzspannung ±UD∕2 an die Eingänge, so tritt diese verstärkt an den Ausgängen auf (Differenzverstärkung, differential gain). Solange man im Aussteuerbereich bleibt, unterdrückt ein Differenzverstärker also die Gleichtaktsignale und verstärkt die Gegentaktsignale. Die MOSFET–Variante tut dies mit sehr hohem Eingangswiderstand.
Die Übertragungskennlinien zeigen eine relativ schlechte Linearität für die npn–Grundschaltung. Hier hilft in der Praxis wieder die Stromgegenkopplung, z. B. zwei gleiche Emitterwiderstände RE, auf Kosten der Differenzverstärkung.
Liegt an den Eingängen eine Spannungsdifferenz UD = 0 an, so ist beim idealen Differenzverstärker Ua1 = Ua2. Beim realen Bauelement beobachtet man aber Ua1 ⇔ Ua2, als ob eine endliche Differenzspannung am idealen Verstärker anliegen würde: Offsetspannung. Die Ursache sind unvermeidbare Unsymmetrien (Toleranzen) in der Schaltung. Zur Korrektur sind verschiedene Massnahmen üblich (Korrekturspannung auf einen Eingang, einen Kollektorwiderstand als Potentiometer, gemeinsamer Emitterwiderstand als Poteniometer, etc). Gute Differenzverstärker haben Offsetspannungen kleiner 1mV und Temperaturdrifts kleiner 1μV∕K.
Der grosse Vorteil monolithischer Differenzverstärkerschaltungen ist ihre Stabilität bei erstaunlicher Einfachheit; die Güte der Stromquelle (z. B. Temperaturkonstanz) ist massgebend.
Nebenbemerkung: Verwendet man statt der Lastwiderstände Stromquellen — einfache Stromspiegel oder Kaskode–Stromspiegel sind üblich —, kann die Differenzverstärkung bzw. das Verstärkungs–Bandbreite–Produkt um etwa eine Grössenordnung gesteigert werden.
 Lizenzinformationen
Lizenzinformationen