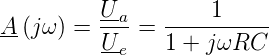

Filterschaltungen sind Baugruppen, die das Frequenzspektrum eines Signals verändern[TS80]. Sie werden verwendet, um zum Beispiel Rauschen zu entfernen, bei drahtloser Übertragung die Trägerfrequenz zu unterdrücken oder um gewisse Komponenten eines Signals zu bevorzugen. Die Filtereigenschaften lassen sich am einfachsten mit analogen Filtern erklären. Darauf aufbauend werden digitale Implementierungen von Filtern besprochen. Die dort erarbeiteten Konzepte können auch bei der Bearbeitung von Datensätzen im Computer verwendet werden.
Als einfachstes Beispiel eines Filters betrachten wir einen RC Tiefpass. Die Filtercharakteristik geschrieben mit Frequenzen ist
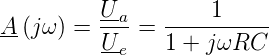 | (2.1) |
Es ist üblich, die Gleichung (2.1) so umzurechnen,
dass die Frequenz Ω, bei der 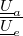 = 2−1∕2 ist, gleich 1
gesetzt wird. Mit Ω =
= 2−1∕2 ist, gleich 1
gesetzt wird. Mit Ω = 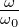 (ω0 =
(ω0 = 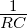 ist die natürlich
Grenzfrequenz unseres Tiefpasses. Gleichung (2.1) wird
dann
ist die natürlich
Grenzfrequenz unseres Tiefpasses. Gleichung (2.1) wird
dann
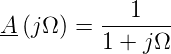 | (2.2) |
Nun haben wir im Abschnitt 2.4.3 über die Laplace-Transformation gesehen, dass diese Kausalität erzwingt. Indem ω mit p identifiziert wird (man kann auch sagen, dass die allgemein komplexe Variable p nur entlang der imaginären Achse betrachtet wird), erhält man die Übertragungsfunktion
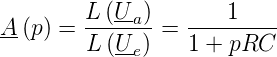 | (2.3) |
und daraus mit P = 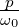 die normierte Darstellung der
Übertragungsfunktion
die normierte Darstellung der
Übertragungsfunktion
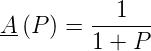 | (2.4) |
Die Darstellung in Gleichung (2.4) ist die einfachste denkbare Darstellung eines Tiefpassfilters. Die Grenzfrequenz ist normiert, alle Details der Realisierung werden mit der Normierung kaschiert. Das Vorgehen ist in gewissem Sinne analog zu dem der theoretischen Physiker, wenn sie ℏ = 1 und c = 1 setzen.
Für Sinuswellen ist das Verhältnis zwischen Ausgangs- und Eingangssignal ist
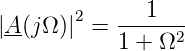 | (2.5) |
Für grosse Frequenzen Ω » 1 verhält sich die
Ausgangsamplitude 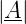 = 1∕Ω. Dies entspricht einem
Verstärkungsabfall von 6 dB pro Oktave (Faktor 2) oder 20
dB pro Dekade (Faktor 10). Der Verstärkungsabfall pro
Dekade ist charakteristisch für die Filterordnung. Pro
Ordnung erhält man 20 dB pro Dekade.
= 1∕Ω. Dies entspricht einem
Verstärkungsabfall von 6 dB pro Oktave (Faktor 2) oder 20
dB pro Dekade (Faktor 10). Der Verstärkungsabfall pro
Dekade ist charakteristisch für die Filterordnung. Pro
Ordnung erhält man 20 dB pro Dekade.
Für einen steileren Abfall der Verstärkung kann man n Filter hintereinander schalten. Wenn man annimmt, dass jeder Teilfilter vom vorhergehenden entkoppelt ist (keine Rückwirkung) und wenn man weiter annimmt, dass jeder Teilfilter eine andere Grenzfrequenz haben kann, charakterisiert durch den Faktor αi dann ist die Übertragungsfunktion
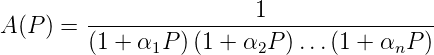 | (2.6) |
Die Koeffizienten αi sind reell und positiv.
Für grosse Frequenzen gilt 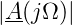 ∝ Ω−n. Der Abfall ist
also n mal 20 dB pro Dekade.
∝ Ω−n. Der Abfall ist
also n mal 20 dB pro Dekade.
Bei n gleichen, entkoppelten Tiefpässen ist die 3-dB Grenzfrequenz Ω = 1, wenn gilt:
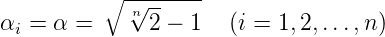 | (2.7) |
Die Grenzfrequenz eines einzelnen Tiefpasses ist um 1∕α höher als die Grenzfrequenz der Gesamtschaltung. Diese Eigenheit ist bei allen zusammengesetzten Teifpässen zu bemerken. Die oben eingeführten Tiefpässe haben nur reelle Pole. Sie heissen kritische Tiefpässe. Tabelle F.1 im Anhang gibt eine Übersicht über die Filterkoeffizienten. Die Koeffizienten sind in Gruppen zu zwei geordnet, da man jedes Polynom mit reellen Koeffizienten in ein Produkt von Polynomen 2. Grades aufspalten kann.
Allgemein ist eine Filterfunktion gegeben durch
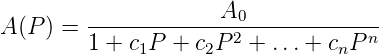 | (2.8) |
Hier ist A0 die Verstärkung bei Ω = 0. Für beliebige reelle Koeffizienten ci kann das Nennerpolynom in Gleichung (2.8) in n∕2 ((n− 1)∕2 bei ungeradem n) Polynome 2. Grades (und ein Polynom ersten Grades bei ungeradem n) aufgespalten werden. Diese Polynome zweiten Grades haben entweder zwei reelle Nullstellen, oder aber zwei konjugiert komplexe. Wir können also schreiben:
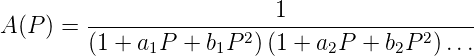 | (2.9) |
Wir vereinbaren, dass bei ungeradem n b1 = 0 sein soll. Für unser kritisch gedämpftes Filter gilt nun:
 | (2.10) |
Diese Koeffizienten sind in Tabelle F.1 aufgelistet.
Konjugiert komplexe Pole, wie sie in einem Filter höherer Ordnung auftreten können, sind nicht mit einfachen RC-Filtern realisierbar. Entweder man verwendet auch Spulen, also RLC-kreise, oder man benötigt aktive Schaltungen, wie sie im Kapitel 3 besprochen werden.
Es gibt nun verschiedene Optimierungsstrategien für die Filterkoeffizienten. Sie werden in den folgenden Abschnitten nun besprochen.
Das Betragsquadrat der Verstärkung eines allgemeinen Tiefpasses hat die Form
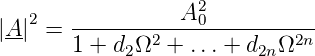 | (2.11) |
Wir fordern nun, dass die Verstärkung möglichst lange gleich A0 sein soll. Das bedeutet, dass der Nenner möglichst lange in der Nähe von 1 sein muss. Dies heisst, dass die verschiedenen Potenzen von Ω so lange wie möglich klein gegen 1 sein müssen. Im Intervall [0…1] ist dies am besten für die höchste Potenz erfüllt. wir setzen also
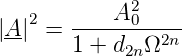 | (2.12) |
Den Koeffizienten d2n kann man aus der Normierungsbedingung
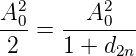 | (2.13) |
bestimmen. Wir erhalten so dass d2i = 0; 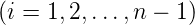 und d2n = 1 ist. Der Nenner der Bestimmungsgleichung ist nun
und d2n = 1 ist. Der Nenner der Bestimmungsgleichung ist nun
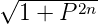 . Die daraus resultierenden Butterworth-Polynome
sind in der Tabelle 2.14 zusammengefasst.
. Die daraus resultierenden Butterworth-Polynome
sind in der Tabelle 2.14 zusammengefasst.
| Ordnung n | Polynom |
| 1 | 1 + P |
| 2 | 1 + 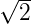 P + P2 P + P2 |
| 3 | 1 + 2P + 2P2 + P3 =
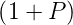 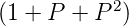 |
| 4 | 1 + 2.613P + 3.414P2 + 2.613P3 + P4 =
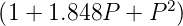 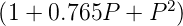 |
| Tabelle 2.14.: | Butterworth-Polynome |
Der Übergang zwischen dem Durchlassbereich und dem Sperrbereich eines Tiefpasses kann man erhöhen, wenn man im Durchlassbereich eine gewisse Welligkeit zulässt. Übliche Polynome haben im Intervall [0…1] eine variable Welligkeit. Tschbyscheff-Polynome haben eine konstante Welligkeit, was man sehr leicht anhand der Definitionsgleichung ersehen kann.
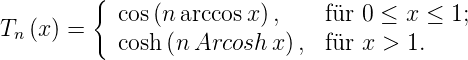 | (2.14) |
Die ersten der resultierenden Polynome sind in Tabelle 2.15 angegeben.
| Ordnung n | Polynom |
| 1 | T1(x) = x |
| 2 | T2(x) = 2x2 − 1 |
| 3 | T3(x) = 4x3 − 3x |
| 4 | T4(x) = 8x4 − 8x2 + 1 |
| Tabelle 2.15.: | Tschebyscheff-Polynome |
Die Tiefpassgleichung ist nun
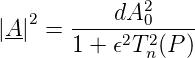 | (2.15) |
Die Normierungskonstanten d und 𝜖 werden so gewählt,
dass für P = 0 die Verstärkung 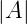 2 = A
02 ist. Ein Vergleich
mit Tabelle 2.15 zeigt, dass für ungerades n d = 1 ist und für
gerades n d = 1 + 𝜖2 ist. Dabei ist 𝜖 ein Mass für die
Welligkeit im Durchlassbereich. Es gelten nun für die
Welligkeit, die minimale und maximale Amplitude:
2 = A
02 ist. Ein Vergleich
mit Tabelle 2.15 zeigt, dass für ungerades n d = 1 ist und für
gerades n d = 1 + 𝜖2 ist. Dabei ist 𝜖 ein Mass für die
Welligkeit im Durchlassbereich. Es gelten nun für die
Welligkeit, die minimale und maximale Amplitude:
Die die Koeffizienten d und 𝜖 werden in der Tabelle 2.16 für verschiedene Welligkeiten verglichen.
| Welligkeit | 0.5dB | 1dB | 2dB | 3dB |
| Amax∕Amin | 1.059 | 1.122 | 1.259 | 1.413 |
| d | 1.112 | 1.259 | 1.585 | 1.995 |
| 𝜖 | 0.349 | 0.509 | 0.765 | 0.998 |
| Tabelle 2.16.: | Koeffizienten der Tschebyscheff-Polynome für verschiedene Welligkeiten |
Die Koeffizienten der Tschebyscheff-Filter können nach Weinberg[Wei62] mit den folgenden Gleichungen berechnet werden:
Dabei ist γ = 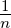 Arsinh
Arsinh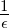 . Das so erhaltene Filter hat alle
gewünschten Eigenschaften, bis auf die Normierung. Wir
verschieben die Frequenzachse um den Faktor α so, dass
. Das so erhaltene Filter hat alle
gewünschten Eigenschaften, bis auf die Normierung. Wir
verschieben die Frequenzachse um den Faktor α so, dass
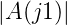 = 1∕
= 1∕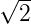 ist. Die wahren Koeffizienten sind dann
ai = αai′ und bi = α2b
i′. Die Tabellen F.4 bis F.7 zeigen die
Filterkoeffizienten. Abbildungen E.7 bis E.10 zeigen die
Frequenzgänge, die en sowie das Phasenbild.
ist. Die wahren Koeffizienten sind dann
ai = αai′ und bi = α2b
i′. Die Tabellen F.4 bis F.7 zeigen die
Filterkoeffizienten. Abbildungen E.7 bis E.10 zeigen die
Frequenzgänge, die en sowie das Phasenbild.
Insbesondere für die Verarbeitung von steilen Impulssignalen ist es wünschenswert, wenn die Durchlaufzeit durch den Filter für alle Frequenzen konstant ist. Diese Durchlaufzeit wird im Alölgemeinen die Gruppenlaufzeit genannt. Die Gruppenlaufzeit ist eine Funktion der Phasenverschiebung (analog zur Gruppengeschwindigkeit bei Wellen).
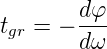 | (2.19) |
Die Phase φ kann aus der Übertragungsfunktion A(jΩ) wie folgt berechnet werden:
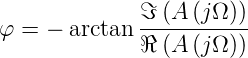 | (2.20) |
Auf die Gruppenlaufzeit eines allgemeinen Filters n-ter Ordnung wollen wir das Butterworth-Konzept anwenden, um eine möglichst konstante Phase zu bekommen. Dazu verwenden wir die normierte Gruppenlaufzeit
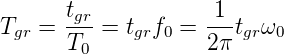 | (2.21) |
Dabei ist f0 die Grenzfrequenz des Filters und T0 = 1∕f0 die dazugehörige Zeitkonstante. Aus Gleichung (2.21) erhält man
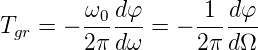 | (2.22) |
Man rechnet nun für ein zu optimierendes Filter die Gruppenlaufzeit aus. Für kleine Frequenzen Ω « 1 sind nur die niedrigsten Potenzen von Bedeutung. Da in jedem Teilprodukt im Nenner und Zähler jeweils Potenzen von Ω2 und Ω4 auftreten, werden die Vorfaktoren von Ω4 nicht berücksichtigt und diejenigen von Ω2 gleichgesetzt. Williams[Wei62] gibt eine Rekursionsformel für die Koeffizienten ci′ der Besselpolynome an.
Die daraus resultierenden Besselpolynome sind in der Tabelle 2.17 angegeben. In der Tabelle F.2 sind die Koeffizienten wie üblich auf die 3-dB Grenzfrequenz umgerechnet. Die Abbildungen im Anhang E zeigen drastisch die unterschiedlichen Gruppenlaufzeiten (und damit die Impulsverzerrungen) der besprochenen Filtertypen.
| n | |
| 1 | 1 + P |
| 2 | 1 + P + 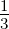 P2 P2 |
| 3 | 1 + P + 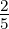 P2 + P2 + 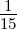 P3 P3 |
| 4 | 1 + P + 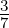 P2 + P2 + 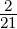 P3 + P3 + 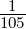 P4 P4 |
| Tabelle 2.17.: | Tabelle der Besselpolynome |
Hochpässe können aus den Tiefpassfilterfunktionen abgeleitet werden, indem man die sogenannte Tiefpass-Hochpass-Transformation anwendet.
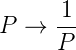 | (2.24) |
Aus der Übertragungsfunktion
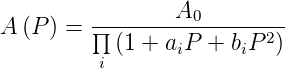 | (2.25) |
wird
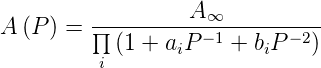 | (2.26) |
Damit können alle oben besprochenen Filtertypen als Hochpässe realisiert werden. Der Abschnitt E.2 im Anhang gibt eine Übersicht über die Übertragungsfunktionen, die Phasenbilder und die Gruppenlaufzeiten.
Bandpässe können aus den Tiefpassfilterfunktionen abgeleitet werden, indem man die sogenannte Tiefpass-Bandpass-Transformation anwendet.
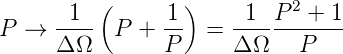 | (2.27) |
ΔΩ ist die Breite des Durchlassbereiches auf dem -3dB-Niveau. ΔΩ hängt mit der Bandbreite B und der Güte Q wie folgt zusammen
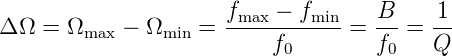 | (2.28) |
Aus der Übertragungsfunktion
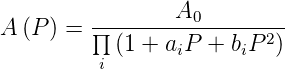 | (2.29) |
wird
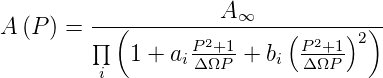 | (2.30) |
Damit können alle oben besprochenen Filtertypen als Bandpässe realisiert werden. Zu beachten ist, dass es für Bandpässe nur gerade Ordnungen gibt. Aus einem Tiefpass 3. Ordnung wird so ein Bandpass 6. Ordnung. Ausser bei einem Bandpass 2. Ordnung kann durch die Wahl der Filterfunktion und der Güte Q die Breite, die Flachheit im Durchlassbereich und die Steilheit getrennt gewählt werden. Der Abschnitt E.3 im Anhang gibt eine Übersicht über die Übertragungsfunktionen, die Phasenbilder und die Gruppenlaufzeiten.
Bandsperren können aus den Tiefpassfilterfunktionen abgeleitet werden, indem man die sogenannte Tiefpass-Bandsperren-Transformation anwendet.
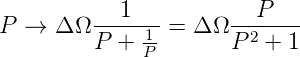 | (2.31) |
ΔΩ ist die Breite des Sperrbereiches auf dem -3dB-Niveau. ΔΩ hängt mit der Bandbreite B und der Güte Q analog zum Bandpass zusammen (Gleichung (2.28)).
Aus der Übertragungsfunktion
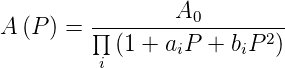 | (2.32) |
wird
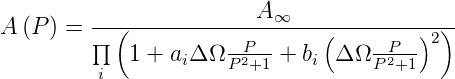 | (2.33) |
Damit können alle oben besprochenen Filtertypen als Bandsperren realisiert werden. Zu beachten ist, dass es für Bandsperren nur gerade Ordnungen gibt. Aus einem Tiefpass 3. Ordnung wird so eine Bandsperre 6. Ordnung. Ausser bei einer Bandsperre 2. Ordnung kann durch die Wahl der Filterfunktion und der Güte Q die Breite, die Flachheit im Durchlassbereich (ausserhalb des Sperrbereiches) und die Steilheit getrennt gewählt werden. Der Abschnitt E.4 im Anhang gibt eine Übersicht über die Übertragungsfunktionen, die Phasenbilder und die Gruppenlaufzeiten.
Wenn gewünscht ist, dass ein Signal zwar verzögert, nicht aber in seiner Amplitude oder Form geändert wird, dann können Allpassfilter eingesetzt werden. Allpassfilter dienen auch als Phasenschieber. Die den Allpassfiltern zugrundeliegende Idee ist die folgende:
Wir setzen also für die Übertragungsfunktion an
mit
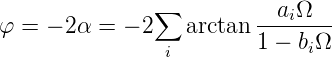 | (2.35) |
Die Koeffizienten werden mit dem Butterworth-Ansatz so berechnet, das die Gruppenlaufzeit über einen möglichst grossen Frequenzbereich konstant bleibt. Im Anhang finden Sie im Abschnitt E.5 die Übertragungsfunktion, das Phasenbild und die Gruppenlaufzeit dieser Filter. Die Filterkoeffizienten sind in Tabelle F.8 angegeben.
Mit der Verfügbarkeit moderner Hochleistungsrechner werden immer öfter Filter auf digitaler Hardware implementiert. Digitale Filter können einerseits analoge Filter nachbilden, sind andererseits auch in der Lage wesentlich kompliziertere Filterfunktionen nachzubilden. Insbesondere sind Bauteiltoleranzen bei digitalen Filtern nicht problematisch. Rundungsfehler können mit mathematischen Methoden abgeschätzt werden. Sie sind dann für alle Implementationen gleich.
Ein digitales Filter wird üblicherweise in einer Umgebung wie in Abbildung 2.43 eingesetzt. Dabei wird das analoge Signal zuerst in ein digitales Signal umgewandelt. Nach der Verarbeitung des so entstandenen Zahlenstromes im digitalen Filter wird mit Digital-Analogwandlern wieder ein analoges Signal erzeugt. Filter am Eingang und am Ausgang sorgen dafür, dass keine unerwünschten Frequenzkomponenten vorhanden sind.
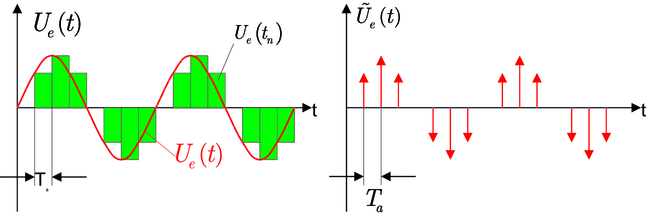
| Abbildung 2.44.: | Analoge Eingangsfunktion und die entsprechende Treppenfunktion (links) und Dirac-Pulsfolge (rechts). |
Das analoge Signal muss zuerst in ein digitales Signal umgewandelt werden. Typische Auflösungen und Frequenzen bei dieser Umwandlung sind 44,1 kHz und 16 Bit bei Audiosignalen, 8 kHz und 12 Bit bei der Telephonie und 13,3 MHz und 8 Bit bei Fernsehsignalen. Abbildung 2.44 zeigt wie aus einem analogen Signal mit einem Abtast-Halteglied eine Treppenfunktion entsteht. Es ist jedoch leichter, anstelle einer Treppe äquivalente Dirac-Impulse zu verwenden. Auch dieses Signal ist in Abbildung 2.44 gezeigt. Mathematisch wird die Folge von Dirac-Impulsen (wir sind immer noch auf der Analogseite) wie folgt beschrieben:
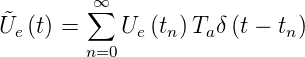 | (2.36) |
Wenn Gleichung (2.36) fouriertransformiert wird, erhält man das Spektrum der Dirac-Pulsfolge.
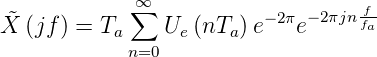 | (2.37) |
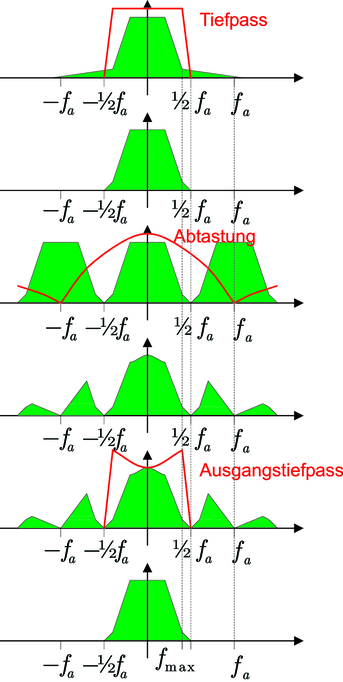
Hier ist fa = 1∕Ta die Abtastfrequenz. Das Spektrum ist periodisch mit der Abtastfrequenz. Aus Abbildung 2.45 ist ersichtlich, dass ein Eingangsspektrum nur dann getreu wiedergegeben werden kann, wenn seine Bandbreite geringer als
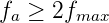 | (2.38) |
ist. Diese Bedingung wird Abtasttheorem genannt. fa∕2 heisst auch die Nyquist-Frequenz. Das Eingangsfilter in Abbildung 2.43 dient zur Verringerung der Bandbreite des Eingangssignals, so dass Gleichung (2.2) erfüllt ist. Das Eingangsfilter kann entweder explizit verwendet werden, oder aber man muss sicherstellen, dass das vorhergehende System keine Frequenzkomponenten über der Nyquistfrequenz abgibt. Um die Konstruktion des Eingangsfilters einfach zu halten, wird meistens anstelle von Gleichung (2.38) die Bedingung fa ≥ 5fmax verwendet. Wenn man bewusst ein schmalbandiges Signal um eine der Vielfachen der Abtastfrequenz digitalisiert und dafür sorgt, dass im eigentlichen Frequenzintervall um 0 keine Signalanteile vorhanden sind, dann ist es möglich ein schnelleres Signal als von der Abtastfrequenz gegeben, zu digitalisieren (Abbildung 2.46). Das Verfahren, Oversampling genannt, wird häufig in Höchstfrequenz-Oszilloskopen eingesetzt.
Die Rückgewinnung des analogen Signals erfordert ebenfalls eine Beschneidung der Bandbreite. Jeder digital-analog-Wandler erzeugt neben dem ursprünglichen Signal auch die um die Vielfachen der Abtastfrequenz gespiegelten Komponenten. Diese müssen mit einem Tiefpassfilter wie in Abbildung 2.43 herausgefiltert werden, es sei denn, man stellt sicher, dass das nachfolgende System wie zum Beispiel bei einem STM diese Funktion übernimmt.
In der Praxis ist es nicht möglich, Dirac-Impulse zu erzeugen. Wenn die Dirac-Pulse durch Pulse der Breite 𝜀Ta ersetzt werden, kann das Eingangssignal als
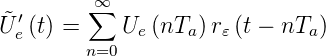 | (2.39) |
geschrieben werden. r𝜀 ist der Rechteckpuls. Als Fouriertransformation erhält man
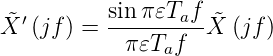 | (2.40) |
Abbildung 2.47 zeigt, dass bei einer geschickten Wahl von 𝜀 die erste Nullstelle der Funktion sinx∕x gerade auf die Abtastfrequenz fällt. Dieser Effekt tritt genau dann auf, wenn 𝜀 = 1 ist, wenn man also eine Treppenfunktion hat. Die Fensterfunktion bewirkt andererseits, dass bei der halben Abtastfrequenz das Signal um den Faktor 0,64 abgeschwächt ist. Man kann also nicht einfach ein Digitalsignal zurückwandeln, ohne den Einfluss der Fensterfunktion zu berücksichtigen. Nach Abbildung 2.48 muss das Tiefpassfilter am Ausgang zur Frequenzgangkorrektur verwendet werden. Alternativ, wenn fa ≥ 5fmax verwendet wird, ist das Filterproblem vielfach zu vernachlässigen. Das bei CD-Spielern als Errungenschaft verkaufte Oversampling dient in erster Linie dazu, Geld bei analogen Ausgangsfiltern zu sparen!
| Abbildung 2.48.: | Darstellung der Änderungen des Frequenzganges bei einer analog-digital-analog-Signalkette |
Der Grundbaustein für ein digitales Filter ist die
Verzögerungsstrecke um das Abtastintervall Ta. Diese
Verzögerungsstrecke tritt auch als Zwischenspeicherung auf,
wenn man im Rechner in einer Schleife Signale berechnet. Die
Folge 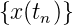 wird in die Folge
wird in die Folge 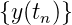 übergeführt
mit
übergeführt
mit
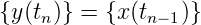 | (2.41) |
Für eine harmonische Folge x(tn) = 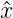 ejωtn gilt
y(tn) =
ejωtn gilt
y(tn) = 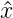 ejωtne−jωTa. Die Übertragungsfunktion eines
Verzögerungsgliedes (auch Totzeitglied genannt) ist also
ejωtne−jωTa. Die Übertragungsfunktion eines
Verzögerungsgliedes (auch Totzeitglied genannt) ist also
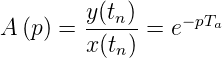 | (2.42) |
Der Frequenzgang eines Verzögerungsgliedes ist also eine periodische Funktion. Das heisst, dass bei Verzögerungsstrecken immer beliebig grosse Phasenverschiebungen auftauchen. Die Phasenverschiebung ist also, im Gegensatz zu der eines Tiefpasses, nicht kompensierbar.
Mit der im Abschnitt 2.4.4.2 eingeführten z-Transformation kann unter Verwendung der Regel
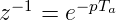 | (2.43) |
erhält man für die digitale Übertragungsfunktion
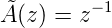 | (2.44) |
Durch Rückeinsetzen erhält man
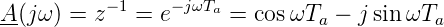 | (2.45) |
Daraus bekommt man für die Amplitude, Phase und Gruppenlaufzeit
also das erwartete Resultat.
Der zweite Baustein für ein digitales Filter ist ein Summationsknoten, der dritte die Multiplikation mit einem konstanten Faktor.
Mit den oben genannten Bauteilen kann ein Tiefpass (Abbildung 2.49) aufgebaut werden. Wir setzen für die Folgen:
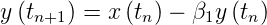 | (2.47) |
Die entsprechende Funktion im z-Raum ist
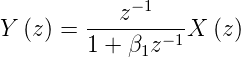 | (2.48) |
Daraus erhält man die Übertragungsfunktion
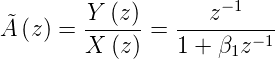 | (2.49) |
Der Frequenzgang kann berechnet werden, indem man
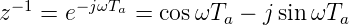 | (2.50) |
setzt. Die Übertragungsfunktion in der Zeit wird demnach
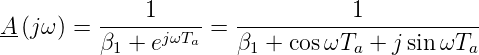 | (2.51) |
Amplitude und Phase sind
Abbildung 2.50 zeigt den Frequenzgang eines Tiefpasses mit β1 = −0, 85. Abbildung 2.51 zeigt die dazugehörige Sprungantwort. Der Frequenzgang ist mit 1∕Ta periodisch. Das Abtasttheorem sagt, dass der Tiefpass nur bis zur Frequenz 1∕2Ta verwendet werden kann.
Ist β1 positiv, erhält man eine Hochpasscharakteristik. Abbildung 2.52 zeigt den Frequenzgang für β1 = 0, 85, Abbildung 2.53 ist die dazugehörige Sprungantwort.
Setzt man β1 = −1 so wird aus dem Tiefpass ein Integrator, wie man unschwer am Frequenzgang in Abbildung 2.50 ersehen kann. Dann gilt
Eingesetzt in den Frequenzgang erhält man
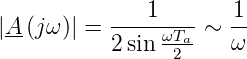 | (2.54) |
was in der Tat der Frequenzgang eines Integrators ist.
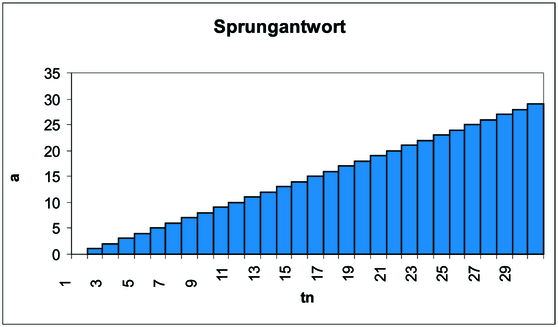
| Abbildung 2.54.: | Der digitale Tiefpass aus Abbildung 2.49 als Integrator. Gezeigt ist die Sprungantwort |
Zentral für ein digitales Filter ist die Verzögerungskette. Für ihre Einbettung in die Filterstruktur gibt es drei mögliche Konfigurationen:
Die Ordnung n des Filters bestimmt auch, dass n Verzögerungsstufen benötigt werden. Hier soll nur die gebräuchlichste Topologie analysiert werden, nämlich die aus Abbildung 2.55. Die Differenzengleichung dafür lautet:
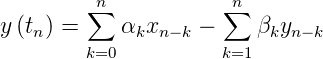 | (2.55) |
Entsprechend berechnet sich aus
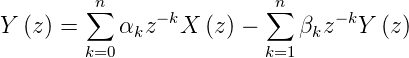 | (2.56) |
ist die Übertragungsfunktion
Die komplexe Übertragungsfunktion kann mit der Identität (2.43) berechnet werden. Weiter normiert man die Frequenz auf die Abtastfrequenz
Das Abtasttheorem verlangt, dass das Eingangssignal nur Frequenzen
Indem man formal für den in der Filterkette nicht vorkommenden Koeffizienten β0 = 1 setzt, erhält man für die Übertragungsfunktion:
![┌ ---------------------------------------
││ [ n∑ ]2 [∑n ]2
││ αk cos 2πkF + αk sin2πkF
|A-(jω)| = ││ [k=n0------------]2---[k=n0------------]2
∘ ∑ βk cos 2πkF + ∑ βk sin 2πkF
k=0 k=0](phys_elektr440x.png) | (2.60) |
Filter können entweder als einen Block berechnet werden, oder aber wie in Abbildung 2.58 kaskadiert werden. Im Falle der Kaskadierung gilt
Der Frequenzgang ist also das Produkt der einzelnen Frequenzgänge, die Ordnung die Summe der einzelnen Ordnungen. Die Kaskadierung vereinfacht die Berechnung der Filterkoeffizienten und die Verifizierung von Filtern Insbesondere bei Filtern mit Rückkopplung ist dies ein wichtiger Punkt.
Man unterscheidet zwei Typen von Filtern
Bei FIR-Filtern sind alle Koeffizienten βi = 0. Die Differenzengleichung lautet also:
Daraus folgt für den z-Raum
![[ ]
Y (z) = α + α z−1 + α z− 2 + ...+ α z− n X (z)
0 1 2 n](phys_elektr443x.png) | (2.63) |
und für die Übertragungsfunktion
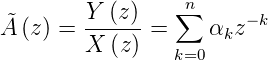 | (2.64) |
Mit Gleichung (2.43) bekommt man den komplexen Frequenzgang
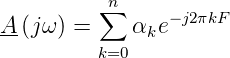 | (2.65) |
Wenn die Filterkoeffizienten Symmetriebedingungen genügen lassen sich besonders einfach zu berechnende Filterstrukturen realisieren. Bei gerader Symmetrie αn−k = αn ist der komplexe Frequenzgang
![− j2πnF ∑n
A-(jω ) = e αk cos[π (n − 2k)F ]
k=0](phys_elektr446x.png) | (2.66) |
Bei ungerader Symmetrie αn−k = −αn erhält man entsprechend
![−j2πnF ∑n
A-(jω) = je αk sin [π (n − 2k )F ]
k=0](phys_elektr447x.png) | (2.67) |
Bei ungerader Symmetrie in gerader Ordnung muss α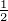 n = 0
sein. Also können Amplitude und Phase explizit angegeben
werden:
n = 0
sein. Also können Amplitude und Phase explizit angegeben
werden:
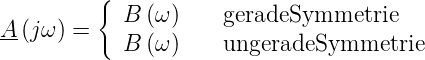 | (2.68) |
Der Betrag der Übertragungsfunktion lässt sich einfach aus den Summen in den Gleichungen (2.66) und (2.66) berechnen. Die Phase ist
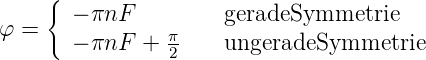 | (2.69) |
In beiden Fällen hängt die Phase linear von der Frequenz ab. Entsprechend ist die Gruppenlaufzeit
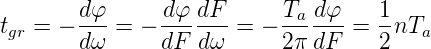 | (2.70) |
Die Gruppenlaufzeit ist für alle FIR-Filter mit symmetrischen Koeffizienten frequenzunabhängig. Symmetrische FIR Filter eingesetzt in Audiogeräten erzeugen keine Laufzeitverzerrungen! Ausser in Ausnahmefällen verwendet man nur FIR-Filter mit linearer Phase.
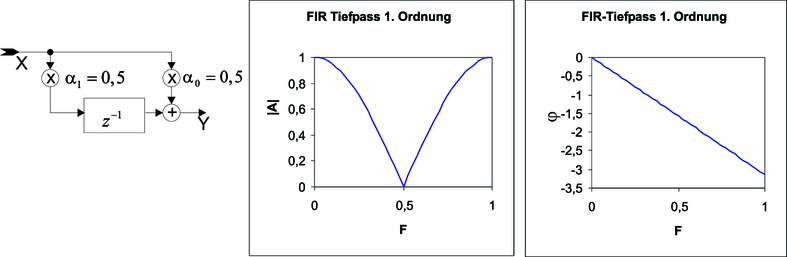
| Abbildung 2.59.: | Ein FIR Tiefpass 1. Ordnung. Links: Schaltschema. Mitte: Frequenzgang. Rechts: Phasengang |
Das in Abbildung 2.59 gezeigte Filter ist ein Tiefpass (Berechnet mit
Excel-Tabelle 1 ).
Für eine Einheitsfolge 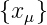 =
= 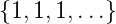 erhält man die
Ausgangsfolge
erhält man die
Ausgangsfolge 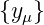 =
= 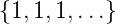 . Die Verstärkung ist hier
also 1. Man berechnet dass die z-Übertragungsfunktion, die
komplexe Übertragungsfunktion, ihr Betrag, die normierte
Grenzfrequenz, die Phase und die Gruppenlaufzeit
. Die Verstärkung ist hier
also 1. Man berechnet dass die z-Übertragungsfunktion, die
komplexe Übertragungsfunktion, ihr Betrag, die normierte
Grenzfrequenz, die Phase und die Gruppenlaufzeit
sind. Eine Analyse der allgemeinen FIR-Übertragungsfunktion zeigt, dass
die Gleichspannungsverstärkung eines FIR-Filters gleich der Summe aller Filterkoeffizienten
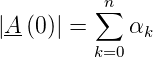 | (2.72) |
ist. Bei der halben Abtastfrequenz, der höchsten nach dem
Nyquist-Theorem zulässigen Frequenz, ist die Eingangsfolge
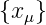 =
= 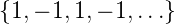 . Das Ausgangssignal ist, wie man
leicht nachprüft, die Nullfolge
. Das Ausgangssignal ist, wie man
leicht nachprüft, die Nullfolge 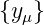 =
= 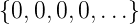 . Auch
diese Eigenschaft ist allgemeingültig.
. Auch
diese Eigenschaft ist allgemeingültig.
Die Verstärkung eines FIR-Filters bei der halben Abtastfrequenz ist gleich der Summe der im Wechsel mit +1 und -1 gewichteten Koeffizienten
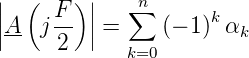 | (2.73) |
Weiter stellt mann fest, dass
wenn man in einem FIR-Filter alle Koeffizienten mit dem gleichen Faktor multipliziert, die Verstärkung um diesen Faktor geändert wird, ohne dass sich die Filtercharakteristik ändert.
Speist man in ein FIR-Filter die Folge 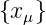 =
= 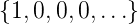 .
ein, so erhält man als Impulsantwort die Folge
.
ein, so erhält man als Impulsantwort die Folge
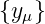 =
= 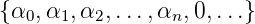 , also gerade die Folge der
Filterkoeffizienten.
, also gerade die Folge der
Filterkoeffizienten.
Die Antwort eines FIR-Filters auf einen Einheitsimpuls ist immer die Folge seiner Filterkoeffizienten. Diese Folge ist bei einem Filter n-ter Ordnung n + 1 Werte lang von null verschieden.
Die Grenzfrequenz des Filters erhält man, indem man
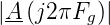 =
=  = cos πFg setzt.
= cos πFg setzt.
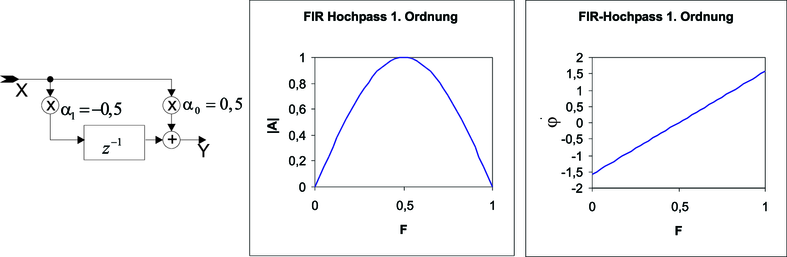
| Abbildung 2.60.: | Ein FIR Hochpass 1. Ordnung. Links: Schaltschema. Mitte: Frequenzgang. Rechts: Phasengang |
Abbildung 2.60 zeigt einen FIR-Hochpass 1. Ordnung (Berechnet mit Excel-Tabelle2 ). Im Unterschied zum Tiefpass ist α1 mit −1 multipliziert. Unsere Regeln sagen, dass die Verstärkung bei der Frequenz null auch null ist, und dass sie bei der halben Abtastfrequenz maximal ist. Im einzelnen sind die Kenngrössen:
Bei tiefen Frequenzen ist die Verstärkung proportional zu F, die Schaltung arbeitet also (was man aus der Gleichung hätte erraten können!) als Differenzierer. Bandpässe und Bandsperren kann man mit einem Filter erster Ordnung, wie bei analogen Filtern, nicht realisieren.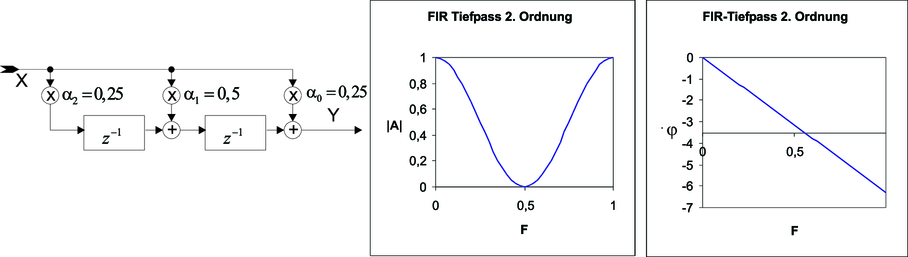
| Abbildung 2.61.: | Ein FIR Tiefpass 2. Ordnung. Links: Schaltschema. Mitte: Frequenzgang. Rechts: Phasengang |
Die Summe der Koeffizienten in der Abbildung 2.61 (Berechnet mit Excel-Tabelle3 ) ist eins, also ist die Verstärkung bei bei der Frequenz null eins. Die Übertragungsfunktion sowie die weiteren Kenndaten sind:
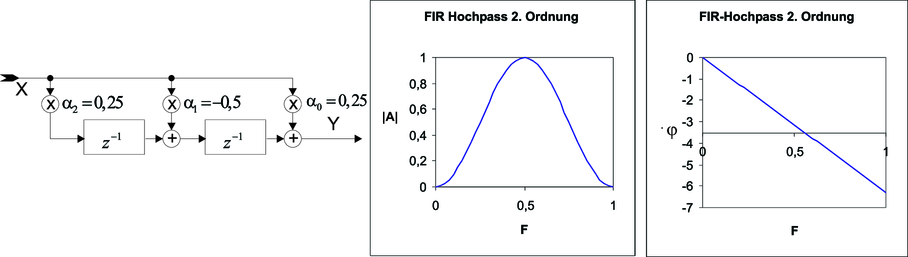
| Abbildung 2.62.: | Ein FIR Hochpass 2. Ordnung. Links: Schaltschema. Mitte: Frequenzgang. Rechts: Phasengang |
Abbildung 2.62 zeigt einen FIR-Hochpass 2. Ordnung (Berechnet mit Excel-Tabelle4 ). Im Vergleich zum Tiefpass zweiter Ordnung ist das Vorzeichen von α1 gewechselt worden. Die Übertragungsfunktion sowie die weiteren Kenndaten sind:
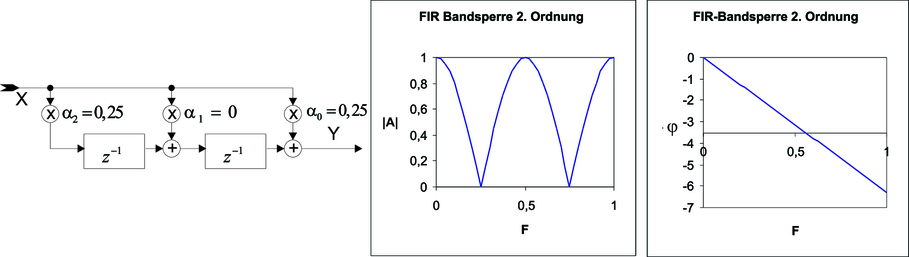
| Abbildung 2.63.: | Eine FIR Bandsperre 2. Ordnung. Links: Schaltschema. Mitte: Frequenzgang. Rechts: Phasengang |
Setzt man α1 = 0 so erhält man aus dem Tiefpass oder Hochpass die in Abbildung 2.63 gezeigte FIR-Bandsperre 2. Ordnung (Berechnet mit Excel-Tabelle5 . Die Übertragungsfunktion sowie die weiteren Kenndaten sind:
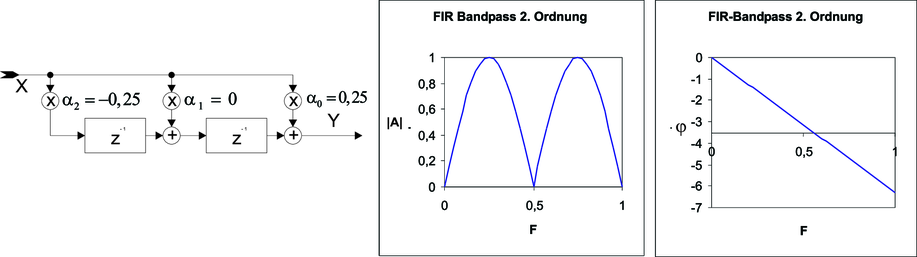
| Abbildung 2.64.: | Ein FIR Bandpass 2. Ordnung. Links: Schaltschema. Mitte: Frequenzgang. Rechts: Phasengang |
Negiert man in der Bandsperre in Abbildung 2.63 α2 so erhält man aus der Bandsperre einen Bandpass (Abbildung 2.64) (Berechnet mit Excel-Tabelle6 . Die Übertragungsfunktion sowie die weiteren Kenndaten sind:
Berechnung der Filterkoeffizienten für FIR-Filter Eine Einführung in die Berechnung der FIR-Filterkoeffizienten kann in Tietze-Schenk[TS80] gefunden werden. Es gibt zwei bevorzugte Verfahren zu dieser Berechnung: die Fenster-Methode und den Remez Exchange Algorithmus. Die zweite Methode ist ein auf Tschebyscheff-Polynomen beruhender Optimierungsalgorythmus, der eine minimale Anzahl von Filterkoeffizienten liefert.
Wie in der Gleichung (2.62) gezeigt wurde, ist die Antwort eines FIR-Filters auf eine Impulsanregung
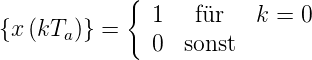 | (2.79) |
Aus (2.79) folgt als Ausgangsfolge die Folge der Koeffizienten.
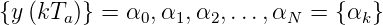 | (2.80) |
Nun sind bei einem linearen System die Impulsantwort und der Frequenzgang durch eine (inverse) Fouriertransformation ineinander überführbar. Für zeitdiskrete Systeme mit fa = 1∕Ta sind die Werte der Impulsantwort für t = kTa durch
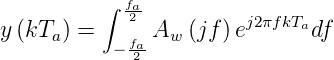 | (2.81) |
aus dem Frequenzgang Aw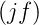 gegeben. man erhält die
gewünschten Koeffizienten, indem man (2.80) und (2.81)
gleichsetzt.
gegeben. man erhält die
gewünschten Koeffizienten, indem man (2.80) und (2.81)
gleichsetzt.
Das resultierende Filter muss nach Tietze und Schenk[TS99] normalisieret und auf die gewünschte Grenzfrequenz umgerechnet werden.
Die zweite Klasse digitaler Filter stellen die rekursiven Filter oder Infinite Impulse Response-Filter dar. Da Ihre Impulsantwort wie die der analogen Filter unendlich lange dauert, kann man die analogen Filter auf die digitalen abbilden.
Zur Abbildung eines analogen Filters auf ein digitales Filter
verwendet man die bilineare Transformation[TS80][LH93]. Um
den Freqenzbereich [0…∞] des analogen Filters auf den
Frequenzbereich [0…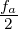 ] des digitalen Filters abgebildet.
] des digitalen Filters abgebildet.
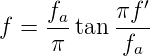 | (2.82) |
Wie gewünscht strebt für f →∞ die digitale Frequenz
f′ → 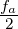 . Dabei ist die Verzerrung der Frequenzachse
umso geringer, je geringer die Frequenz im Vergleich zur
Taktfrequenz ist. Wir rechnen wieder mit normierten
Frequenzen
. Dabei ist die Verzerrung der Frequenzachse
umso geringer, je geringer die Frequenz im Vergleich zur
Taktfrequenz ist. Wir rechnen wieder mit normierten
Frequenzen
Die Transformationsgleichung für die normierten Frequenzen ist dann
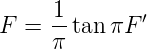 | (2.84) |
Bei der Transformation eines Tschebyschefftiefpasses
(Abbildung 2.65) bleibt das charakteristische Überschwingen
erhalten. Damit die Grenzfrequenz des ursprünglichen
Tiefpasses und des neuen Tiefpasses gleich bleibt, ersetzen wir
in Gleichuing (2.84) den Vorfaktor  .
.
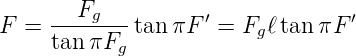 | (2.85) |
Man erkennt in Abbildung 2.65, dass nun der Frequenzgang des digitalen Filters erst über der Grenzfrequenz Fg abweicht. Die Variable P in der normierten Übertragungsfunktion wird
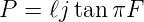 | (2.86) |
Unter Verwendung der Umformung
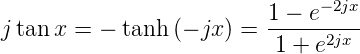 | (2.87) |
sowie mit der Definition von z ist
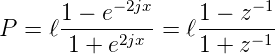 | (2.88) |
Die Form der obigen Gleichung erklärt den Namen ¨Bilineare Transformation¨. Sie bildet den Arbeitsbereich eines analogen Filters auf den eines digitalen ab. Abweichungen sind desto geringer, je grösser die Abtastfrequenz fa im Vergleich zu den interessierenden Frequenzen ist. Aus
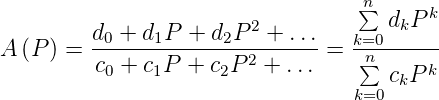 | (2.89) |
Wenn man die bilineare Transformation oben einsetzt, erhält man
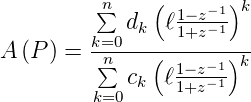 | (2.90) |
Durch Koeffizientenvergleich erhält man schliesslich die Koeffizienten der Digitalfilter
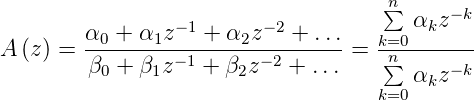 | (2.91) |
Für das in der Abbildung 2.66 dargestellte IIR-Filter erster Ordnung soll der analoge Frequenzgang (schliesst alle Filterarten ein)
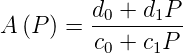 | (2.92) |
auf das IIR-Filter
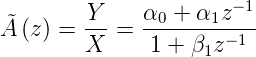 | (2.93) |
Der Koeffizientenvergleich ergibt
Die obigen Gleichungen angewandt auf einen allgemeinen
Tiefpass A(P) = 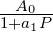 ergeben
ergeben
Der Hochpass A(P) = 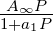 wird in der digitalen
Implementation
wird in der digitalen
Implementation
Bei einem digitalen Filter wird die Grenzfrequenz durch die Abtastfrequenz festgelegt. Dies bietet eine einfache Möglichkeit der Abstimmung des Filters.
Die allgemeine Form eines analogen Filters zweiter Ordnung
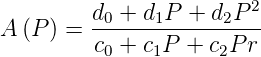 | (2.97) |
wird durch die bilineare Transformation zu
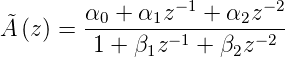 | (2.98) |
der Übertragungsfunktion des digitalen IIR-Filters aus Abbildung 2.67. Die Koeffizienten sind:
Aus dem Tiefpass A(P) = 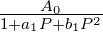 erhält man das
äquivalente IIR Filter mit den Koeffizienten
erhält man das
äquivalente IIR Filter mit den Koeffizienten
Der Hochpass A(P) = 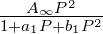 wird zu
wird zu
Weiter wird der Bandpass A(P) = 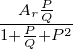 transformiert
in
transformiert
in
Die Bandsperre A(P) = 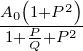 transformiert sich
in
transformiert sich
in
Endlich wird aus dem Allpass A(P) = 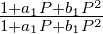 das
folgende digitale IIR-Filter
das
folgende digitale IIR-Filter
 Lizenzinformationen
Lizenzinformationen