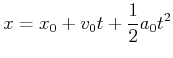Weiter: Literatur Oben: Einleitung Zurück: Fehler  Skript:  PDF-Datei Übungen:  Blätter

Dimensionsanalyse

Dieser Stoff wurde am 16.10.2001 behandelt

(Siehe Tipler, Physik[Tip94, 5]) (Siehe Gerthsen, Physik[GV95, 2])

Die Dimension zeigt, wie eine Grösse von den Basisgrössen, z.B. Länge, Zeit und Masse abhängt. Wie man nicht Äpfel mit Birnen verrechnen kann, müssen bei einer physikalischen Gleichung die Dimensionen auf beiden Seiten übereinstimmen. Die Dimensionsanalyse ist ein mächtiges Werkzeug, um zu testen, ob man richtig gerechnet haben könnte¹.

Beispiel

$$x = x_0 + v_0 t + \frac{1}{2} a_0 t^2$$ (2.7)

Gleichung (2.7) ist richtig, wenn man wie unten für die Länge $L$ und für die Zeit $T$ einsetzt.

$$L = [X] = L = [x_0] = \frac{L}{T}T = [v_0 t] = \frac{L}{T^2} T^2 = [\frac{1}{2} a_0 t^2]$$ (2.8)

Beispiel: Schwingungsdauer eines Pendels

Die Schwingungsdauer $t$ hängt von der Länge $\ell$, der Masse $m$ und der Erdbeschleunigung $g$ ab. Also ist

$$t \approx m^\alpha l^\beta g^\gamma$$ (2.9)

oder

$$T^1 = M^\alpha L^\beta \left(\frac{L}{T^2}\right)^\gamma = L^{\beta+\gamma} M^\alpha T^{-2\gamma}$$ (2.10)

Der Exponentenvergleich ergibt $\alpha = 0$, $\gamma = -\frac{1}{2}$ und damit $\beta = \frac{1}{2}$. Wir erraten, dass die Schwingungsdauer eines Pendels wie

$$t \approx \sqrt{\frac{l}{g}}$$ (2.11)

ist, das korrekte Resultat, wenn man von Vorfaktoren absieht.

 Skript:  PDF-Datei Übungen:  Blätter