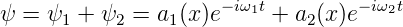

Die Eigenwerte des Hamiltonoperators sind die Energieeigenwerte des betrachteten Systems. In den nächsten Abschnitten sollen die Energieeigenwerte der Schrödingergleichung für verschiedenen Potentialfunktionen berechnet werden.
Messbar sind nur Erwartungswerte eines Operators und eines Zustandes charakterisiert durch die Wellenfunktion ψ. Nach Gleichung (5.26) kann die Wellenfunktion ψ immer mit einem konstanten Phasenfaktor multipliziert werden, ohne dass sich der Erwartungswert ändert, da dieser Phasenfaktor den Beitrag eiαe−iα = 1 gibt. Wenn der Zustand eines Systems ψ eine ortsabhängige Linearkombination zweier Eigenfunktionen ψ1 = a1(x) exp(−iω1t) und ψ2 = a2(x) exp(−iω2t) ist, wobei a1(x),a2(x) ∈ℂ und ein gemeinsamer Phasenfaktor eiα, α ∈ℝ, auftreten kann, gilt
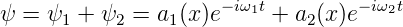 | (5.1) |
Wenn die Wellenfunktionen ψ1 und ψ2 zweier Zustände sich zeitlich nicht ändern, dann nennt man sie stationär und die Wahrscheinlichkeitsdichten p1 = ψ1∗·ψ 1 und p2 = ψ2∗·ψ 2 haben zeitlich sich nicht ändernde Werte. Im Dialekt der Quantenphysiker nennt man das scharfe Werte. Die entsprechenden Eigenwerte sind zeitunabhängig.
Obwohl die Funktionen ψ1 und ψ2 stationäre Zustände sein sollen, also zeitlich unveränderlich, ist die Summe ψ nicht stationär. Die kurze Rechnung
Die Wahrscheinlichkeitsdichte ψ∗ψ ist also zeitlich nicht konstant, das heisst nicht stationär. Es gibt keinen zeitlich konstanten Energieeigenwert zu dieser Funktion.
Zustände, die Eigenzustände des Energieoperators
 = iℏ = iℏ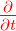 sind, ändern sich mit der Zeit nicht. Sie
werden stationäre Zustände genannt. sind, ändern sich mit der Zeit nicht. Sie
werden stationäre Zustände genannt. |
Der Hamiltonformalismus der klassischen Mechanik eines
Systems mit der Lagrangefunktion L beschreibt die
mechanischen Bewegungsgleichungen mit verallgemeinerten
Ortskoordinaten qi und verallgemeinerten Impulskoordinaten
pi = ∂L∕∂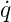 i. Die Variablen qi und pi werden üblicherweise
kanonische konjugierte Variablen genannt.
i. Die Variablen qi und pi werden üblicherweise
kanonische konjugierte Variablen genannt.
In Quantenmechanik gibt es ein analoges Konzept zu kanonisch konjugierten Variablen, die kanonisch konjugierten Operatoren. Dies sind
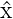 und Impuls
und Impuls 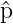 x
x
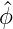 und Drehimpuls
und Drehimpuls 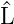
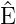 (Die Zeit t ist in der
Quantenmechanik eine klassische Variable, kein
Operator.)
(Die Zeit t ist in der
Quantenmechanik eine klassische Variable, kein
Operator.)Die Definitionen der Operatoren sind
wobei 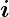 ,
, 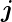 und
und 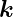 die Einheitsvektoren sind, die das
Koordinatensystem aufspannen.
die Einheitsvektoren sind, die das
Koordinatensystem aufspannen.
Analog zur Poissonklammer der klassischen Mechanik gibt es in der Quantenmechanik Kommutatoren.
Die mathematische Operation
![[ ]
^A,B^ = ^A ^B − ^B ^A](ap-2015387x.png) heisst Kommutator. |
So wie die Operatoren in der Quantenmechanik definiert sind, gelten die folgenden Vertauschungsrelationen:
Die Vertauschungsrelationen von konjugierten Operatoren heissen auch Unschärferelationen. Sie sind eine Konsequenz der Wellennatur der Lösungen der Schrödingergleichung und wurden von Werner Heisenberg gefunden. Die Energie-Zeit-Unschärferelation gilt oftmals nicht als echte Unschärferelation, da die Zeit kein Operator ist.
 Lizenzinformationen
Lizenzinformationen