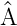 beschrieben sein; der Wert
dieser Grösse A ist ein Eigenwert des Operators
beschrieben sein; der Wert
dieser Grösse A ist ein Eigenwert des Operators 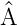 .
.
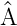 beschrieben sein; der Wert
dieser Grösse A ist ein Eigenwert des Operators
beschrieben sein; der Wert
dieser Grösse A ist ein Eigenwert des Operators 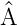 .
.Weiter gilt: Wenn der Zustand eines Systems durch eine Wellenfunktion ψ = ∑ kckfk dargestellt wird, wobei die fk Eigenfunktionen des gleichen hermiteschen Operators und die ck komplexe Konstanten sind, dann ist
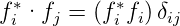 | (5.1) |
und
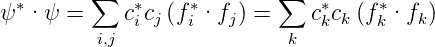 | (5.2) |
Die Eigenwerte ak von 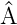 sind reelle Zahlen (ak ∈ℝ ∀k). Die
Wellenfunktionen ψk, definiert durch
sind reelle Zahlen (ak ∈ℝ ∀k). Die
Wellenfunktionen ψk, definiert durch 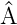 ψk = akψk oder
ψk = akψk oder
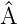
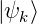 = A
= A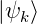 , sollen ein vollständiges Funktionensystem
bilden.
, sollen ein vollständiges Funktionensystem
bilden.
Der Erwartungswert des Operators 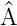 und damit der durch
ihn beschriebenen Grösse A ist
und damit der durch
ihn beschriebenen Grösse A ist
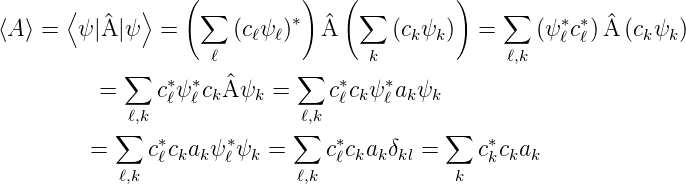 | (5.3) |
Der Erwartungswert 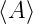 ist eine statistische Grösse.
Analog zu Mittelwerten einer Stichprobe gibt es als Mass der
Verschmierung das Analog zur Standardabweichung. In
Allgemein ist die Streuung einer Observablen A analog
definiert wie
ist eine statistische Grösse.
Analog zu Mittelwerten einer Stichprobe gibt es als Mass der
Verschmierung das Analog zur Standardabweichung. In
Allgemein ist die Streuung einer Observablen A analog
definiert wie
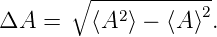 | (5.4) |
 Lizenzinformationen
Lizenzinformationen