__________________________________________________________________________
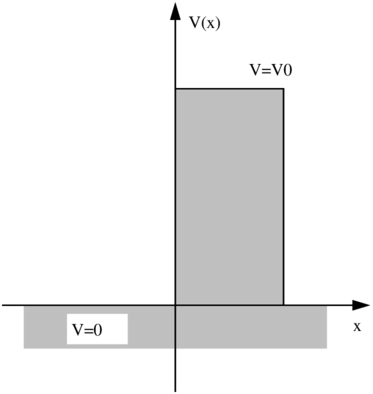
Potentialwand.
_____________________________________________________________________

__________________________________________________________________________

Potentialwand.
_____________________________________________________________________
Wir sahen, dass eine von links einlaufende Welle mit einer kinetischen Energie kleiner als die Stufenhöhe im Bereich der Stufe eine exponentiell abfallende Wahrscheinlichkeit besitzt. Ist die Stufe endlich breit, so gibt es auch am rechten Rand der Stufe eine Aufenthaltswahrscheinlichkeit: das Teilchen hat die Barriere durchtunnelt. Zur Rechnung verwenden wir den Ortsanteil der Wellenfunktion ψ(x,t) = ϕ(x) exp(−iωt), die von links her in positiver Richtung auf die Barriere zwischen x = 0 und x = a (Abbild. 5.9) einfallen soll.
Wie im vorherigen Absatz muss ϕ und ∂ϕ∕∂x stetig sein. Die Energie der Welle ist zuerst beliebig.
Da für x < 0 und x > a das Potential V (x) = 0 ist, ist k1 = k3. Für x = 0 und x = a sind die Stetigkeitsbedingungen
Wir haben sechs Unbekannte und vier Gleichungen. A1 ist beliebig wählbar, da wir eine von links einlaufende Welle annehmen. A′3 = 0 weil keine von rechts einlaufende Welle existiert. Damit bleiben vier Unbekannte für vier Gleichungen. Die Stetigkeitsbedingungen sind dann
Die Lösungen sind:
Aus diesen Beziehungen folgen mit
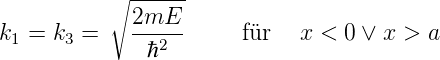 | (5.5) |
und
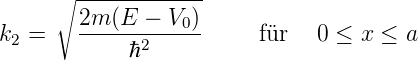 | (5.6) |
die Transmissions- und Reflexionskoeffizienten T und R
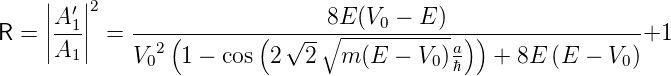 | (5.7) |
und
wobei k1 = k3 = 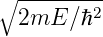 und k2 =
und k2 = 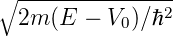 sind. Eine kurze Kontrolle zeigt, dass R + T = 1 ist,
wir also keine Teilchen verlieren. Sowohl die Reflexion
wie auch die Transmission oszillieren mit der Breite der
Barriere a. Die Gleichungen können noch vereinfacht
werden:
sind. Eine kurze Kontrolle zeigt, dass R + T = 1 ist,
wir also keine Teilchen verlieren. Sowohl die Reflexion
wie auch die Transmission oszillieren mit der Breite der
Barriere a. Die Gleichungen können noch vereinfacht
werden:
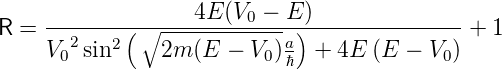 | (5.9) |
und
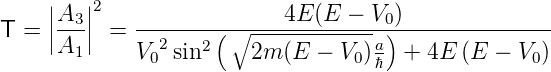 | (5.10) |
Wenn E < V 0 ist, wird aus dem Cosinus ein Cosinus hyperbolicus und die Gleichungen lauten
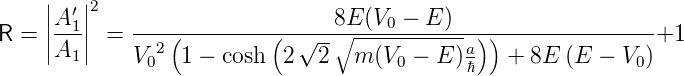 | (5.11) |
und
Auch diese Gleichungen können vereinfacht werden
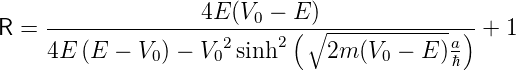 | (5.13) |
und
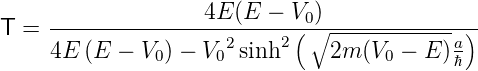 | (5.14) |
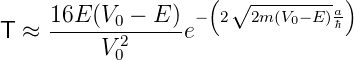 | (5.15) |
Wenn sich ein Elektron mit der Energie E = 1 eV auf einen Potentialwall mit Breite a = 100 pm und der Höhe V 0 = 2 eV hinzu bewegt, dann ist die Transmissionswahrscheinlichkeit T ∼ 0.777454. Die Näherung nach Gleichung (5.15) ergäbe 1.435712, ein unphysikalischer Wert. Für eine Barrierenbreite von 500 pm wäre T = 0.0235471, die Näherung 0.0238285. Je dicker die Barriere, desto besser ist die exponentielle Näherung. Unter den gleichen Bedingungen hätte ein Proton (mp ≃ 1836.153me) durch eine Barriere von a = 100 pm eine Transmissionswahrscheinlichkeit von T ≈ 3.4195·10−19 und bei a = 500 pm wäre T ≈ 1.8264·10−95. Das heisst, dass der Tunneleffekt für atomare Distanzen für Elektronen wahrscheinlich, für Protonen sehr unwahrscheinlich ist.
Dieser Befund wird durch die aus der Chemie bekannte Tatsache, dass Elektronen die Bindungen vermitteln, gestützt. Tunneln für Protonen ist nur auf der Längenskala von Kernen (1 fm) wahrscheinlich.
Das Rastertunnelmikroskop (STM) beruht auf dem Tunneleffekt für Elektronen. Diese können eine kurze Potentialbarriere durchqueren. Dabei verringert sich der Tunnelstrom exponentiell mit der Breite der Barriere.
__________________________________________________________________________
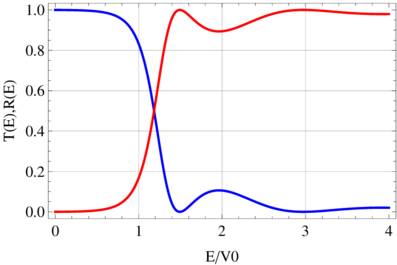
Transmissionskoeffizient (rot) und Reflexionskoeffizient (blau)
_____________________________________________________________________
Abbildung 5.9 zeigt auf einer skalenfreien Darstellung den Verlauf des Transmissions- und des Reflexionskoeffizienten für eine feste Barrierenbreite und in Abhängigkeit der Energie des einlaufenden Teilchens skaliert mit der Barrierenhöhe V 0. Für E∕V 0 haben wir den erwarteten ungefähr exponentiellen Verlauf. Im Durchlassbereich (E∕V 0 > 1) zeigen sich jedoch Resonanzen. Bei E∕V 0 = 1.5 ist die Transmission minimal. Der Effekt ist analog zu den Phänomenen, die man beobachtet, wenn sich eine Wasserwelle über eine Untiefe[Wik15] hinweg bewegt.
__________________________________________________________________________
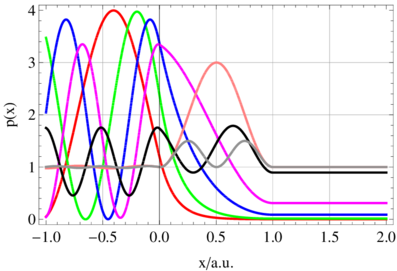
Wahrscheinlichkeitsdichten an der Tunnelbarriere der skalenfreien Breite a = 1. Rot: E∕V 0 = 0.3, grün: E∕V 0 = 0.6, blau: E∕V 0 = 0.9, magenta: E∕V 0 = 1.1, pink: E∕V 0 = 1.5 (Resonanz, Reflektivität minimal, Transmission maximal), schwarz: E∕V 0 = 2.0 (maximale Reflektivität), grau: E∕V 0 = 3.0.
_____________________________________________________________________
Abbildung 5.9 zeigt für verschiedene Relativenergien E∕V 0 die Wahrscheinlichkeitsdichten für den Aufenthalt. Beachten Sie insbesondere die Welle für E∕V 0 = 1.5!
 Lizenzinformationen
Lizenzinformationen