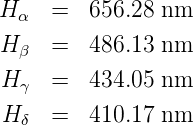

| Versuch zur Vorlesung: | |
| Balmer-Serie (Versuchskarte AT-35) | |
Johann Jakob Balmer entdeckte 1885 im Spektrum der Sonne eine Serie von Absorptionslinien, die bei den Wellenlängen
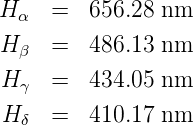
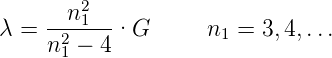 | (6.1) |
gegeben sei, mit G = 364.5 nm.
Wenn wir Gleichung (6.1) mit spektroskopischen Wellenzahlen
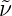 =
= 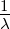 ausdrücken, erhalten wir
ausdrücken, erhalten wir
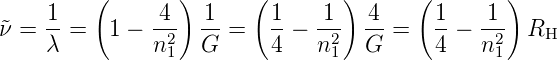 | (6.2) |
Die Grösse RH = 4∕G = 1.09739·107 m−1 ist die
Rydbergkonstante für Wasserstoff. Gleichung (6.1) oder
Gleichung (6.2) können so umgeschrieben werden, dass die
Frequenz ν und nicht die Wellenlänge λ berechnet wird. Mit
ν·λ = c oder ν = c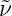 erhalten wir
erhalten wir
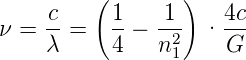 | (6.3) |
Die Zahl 4 ermuntert, sie als n22 zu schreiben mit n 2 = 2. Also erhalten wir
mit n2 < n1. Zwischen der Rydbergkonstante RH′ für Frequenzen und der Rydbergkonstante RH für Wellenzahlen gibt es die Beziehung
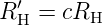 | (6.5) |
Die theoretischen und gemessenen Werte von RH und RH′ sind
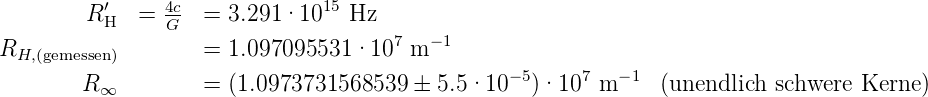
Mit RX bezeichnet man die Rydbergkonstante für die Atomsorte X. R∞ ist die Rydbergkonstante für unendlich schwere Atome.
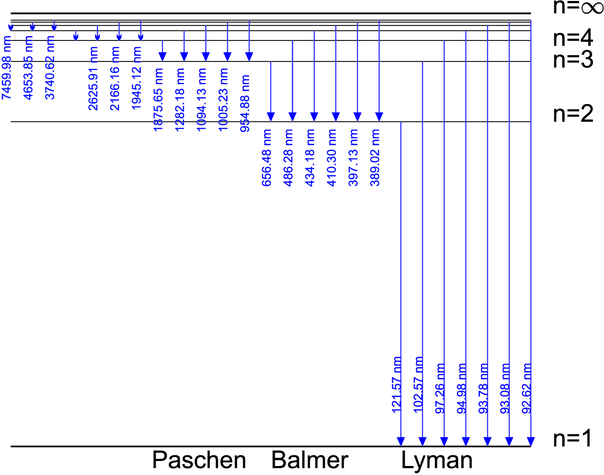
Setzt man in Gleichung (6.4a) oder Gleichung (6.4b) n2 = 2 so erhält man wieder die Balmer-Serie. Die kürzeste durch Gleichung (6.4a) vorhergesagte Wellenlänge einer Absorptionslinie liegt bei der Seriengrenze bei λ∞ = 91 nm. Neben der Balmer-Serie existieren die kürzerwellige Lyman-Serie (n2 = 1) sowie die längerwelligen Paschen-Serie (n2 = 3), Brackett-Serie (n2 = 4) und Pfund-Serie (n2 = 5).
__________________________________________________________________________
_____________________________________________________________________
Abbildung 6.1 zeigt die Lage der Lyman-, Balmer- und Paschen-Serien im Wasserstoffspektrum. Bei Gasentladungslampen können diese Linien als Emissionslinien beobachtet werden. Da die Temperatur der Sonne so hoch ist, dass ihr Emissionsmaximum als thermischer Strahler im Grünen liegt, werden die Emissionslinien überstrahlt. Emission ist aber immer mit Absorption verbunden, so dass auf der Sonne die Absorptionslinien gemessen werden können.
Die Differenzfrequenz zweier Linien aus einer der Serien ist wieder eine beobachtete Linie im Absorptionsspektrum. Dies kann man aus
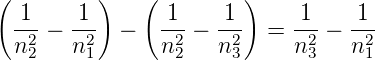 | (6.6) |
ersehen. Aus der Existenz der Wasserstofflinien folgt, dass Elektronen im Wasserstoffatom H nur diskrete Energien einnehmen können, die sogenannten diskreten Energieniveaus.
Um die optisch-spektroskopischen Eigenschaften von Atomen zu erklären, nahm Niels Bohr an, dass sich Elektronen auf Kreisbahnen wie bei Kopernikus bewegten. Arnold Sommerfeld erweiterte dieses Modell, indem er Kepler-Bahnen annahm. Er konnte damit auch Drehimpulsphänomene erklären.
Elektronen, die sich nach Bohr auf kreisförmigen Planetenbahnen bewegen, werden durch die Coulombkraft auf der Bahn gehalten. Die Zentripetalkraft ist das Gleiche wie die Coulombkraft. Die Zentripetalkraft gibt die notwendige Stärke einer Kraft an, die ein Teilchen auf einer Bahn mit gegebenem Krümmungsradius hält.
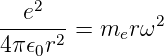 | (6.7) |
Über kinetische und potentielle Energien können die folgenden Aussagen getroffen werden:
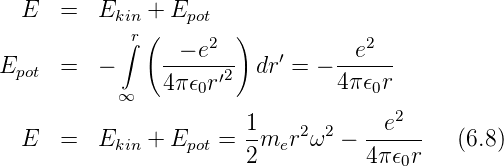
E ist die Gesamtenergie. Sie ist für gebundene Zustände kleiner null. Aus Gleichung (6.7) folgt
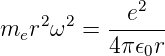 | (6.9) |
und damit für die Energie
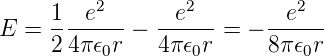 | (6.10) |
Andererseits folgt auch aus Gleichung (6.7) auch das dritte Keplergesetz (verknüpft grosse Halbachsen und Umlaufszeiten)
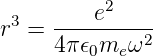 | (6.11) |
Aus Gleichung (6.11) erhalten wir für den inversen Bahnradius
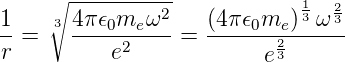 | (6.12) |
und für die Energie
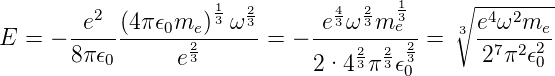 | (6.13) |
Aus dieser klassischen Rechnung haben wir eine Beziehung für den Bahnradius und die Energie als Funktion der Kreisfrequenz der Anregung bekommen. Diese klassische Rechnung hat die folgenden Probleme:
Niels Bohr postulierte in seinen Arbeiten zur Quantentheorie [Boh13, Boh15, Boh18, Boh20] von 1913, dass
Der Energieunterschied zwischen zwei Bahnen bei unendlich schwerem Kern kann mit der Balmerformel und der Rydbergkonstante ausgedrückt werden:
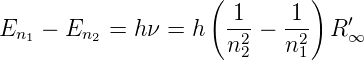 | (6.14) |
Aus Gleichung (6.14) folgt
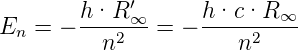 | (6.15) |
Nach Niels Bohr ist die Umlauffrequenz gleich der emittierten Frequenz. Sommerfeld ergänzte die Theorie, indem er elliptische Bahnen einführte. So konnte er auch Bahndrehimpulseffekte beschreiben. Wenn die Quantenmechanik eine übergreifende Theorie sein soll, dann muss sie als Grenzfall die klassische Theorie beinhalten. Diese Aussage wird das Korrespondenzprinzip genannt.
| Korrespondenzprinzip: Im Grenzfall grosser Energien und kleiner Energiedifferenzen muss die Quantenmechanik (und jede moderne Theorie) in die klassische Mechanik übergehen. |
Die Bohr-Sommerfeldtheorie war unbefriedigend, da sie durch klassische Physik mit einigen ad-hoc Annahmen quantenmechanische Phänomene beschreiben wollte.
Wir betrachten zwei Zustände n1 » 1 und n2 = n1 + τ mit τ ∈ ℕ. Wir betrachten also benachbarte Bahnen und nehmen an, dass der Kern unendlich schwer sei. Mit der Rydberggleichung erhalten wir
Bei benachbarten Bahnen (τ = 1), hohen Energien (n1 » 1) und sehr schweren Kernen erhalten wir für die Frequenz des absorbierten oder emittierten Lichtes
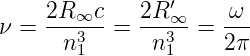 | (6.17) |
Mit Gleichung (6.17) kann Gleichung (6.13) umgeschrieben werden
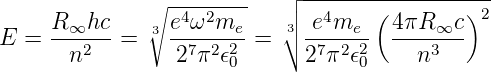 | (6.18) |
Die folgende Umrechnung führt zu einer Gleichung mit der Elektronenmasse (Achtung! die Definition der Rydbergkonstante R∞ beinhaltet die Elektronenmasse, nicht die reduzierte Elektronenmasse (Zweikörperproblem!) und der Elektronenladung
| Aus den Abständen der Wasserstofflinien in Rydbergzuständen (ni » 1) kann man RH bestimmen und daraus mit Gleichung (6.19) h, e oder μe, die reduzierte Masse, und daraus die Elektronenmasse me berechnen, wenn die Protonenmasse mP und die relativistischen Massendefekte bekannt sind. |
Aus der Energie-Gleichung (6.10) und der Definition der Rydbergkonstante R∞ aus Gleichung (6.19) erhalten wir mit
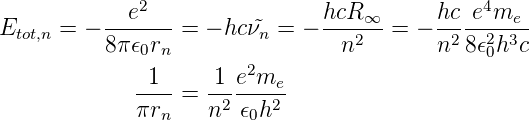
Damit wird der Radius der n-ten Bahn bei unendlich schweren Kernen
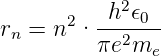 | (6.20) |
n wird die Hauptquantenzahl genannt. Die Hauptquantenzahl ist mit dem Bahnradius und der dazu gehörigen Energie verknüpft. Genaue Messungen zeigten schon Anfang des 20. Jahrhunderts, dass Abweichungen existieren, dass die physikalische Beschreibung der Absorption und der Emission von Licht durch das Wasserstoffatom nach Balmer und Rydberg noch nicht vollständig war.
Die Spektren können präziser beschrieben werden, wenn nach Sommerfeld auch der Bahndrehimpuls berücksichtigt wird. Der Bahndrehimpuls ist
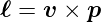 | (6.21) |
Bei Kreisbahnen stehen 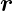 n und
n und 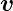 senkrecht aufeinander.
Gleichung (6.21) kann deshalb mit Gleichung (6.19)
umgeschrieben werden
senkrecht aufeinander.
Gleichung (6.21) kann deshalb mit Gleichung (6.19)
umgeschrieben werden
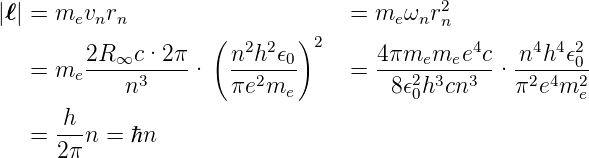
Also sollte bei Kreisbahnen
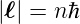 | (6.22) |
sein. Dies ist jedoch nicht der Fall, da wir mit dem theoretischen Wert der spektralen Grösse R∞ gerechnet hatten und nicht mit der atommassenabhängigen Rydbergkonstante. Effektiv zählt nur die reduzierte Masse, und diese hängt von der Ordnungszahl des Atoms und dem Ladungszustand ab. Die reduzierte Masse ist
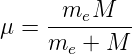 | (6.23) |
wobei me die Elektronenmasse und M die Masse des Kerns plus aller weiterer Elektronen ist.
Das heisst, dass die gemessene Rydbergkonstante RH
ungleich der vorher in Gleichung (6.19) berechneten
Rydbergkonstante R∞ ist. Aus R∞ = 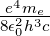 bekommen
wir
bekommen
wir
Nun ist die Masse eines Elektrons me = 9.1·10−31 kg, die eines Protons mp = 1.67·10−27 kg. Das heisst, dass für ein Wasserstoffatom die relative Änderung der Rydbergkonstante
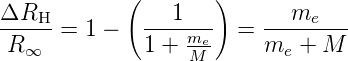 | (6.25) |
Wir erhalten

Diesen aus der Tabelle ersichtlichen Effekt nennt man den Isotopeneffekt. Man sieht, dass zwischen 3 1H und 3 2He optisch spektroskopisch unterschieden werden kann. Der Unterschied ist zwar auf der 7. Stelle nach dem Komma, aber immer noch gross gegen die bis zu 14 Stellen Genauigkeit der optischen Spektroskopie. Zum Vergleich ist noch das Myonium gezeigt, ein wasserstoffähnliches Gebilde, bei dem das Proton durch ein Anti-Myon ersetzt wurde.
Dieser spektroskopische Unterschied besteht auch zwischen 92
235U
und 92
238U . Bei 92
235U wäre ΔR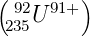 ∕R∞ = 2.31557·10−6,
bei 92
238U wäre
∕R∞ = 2.31557·10−6,
bei 92
238U wäre
ΔR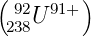 ∕R∞ = 2.28637·10−6. Diese Unterschiede in den
Absorptionswellenlängen durch den Isotopeneffekt werden
in einem neuartigen Verfahren zur Isotropentrennung
(SILEX) verwendet (siehe Mitteilung der DPG
http://www.dpg-physik.de/veroeffentlichung/physik_konkret/pix/Physik_Konkret_11.pdf).
Dieses Verfahren ist ein Hochrisikoverfahren, weil die
notwendigen Apparaturen im Keller eines Einfamilienhauses
Platz haben. So kann die Urananreicherung nicht mehr
kontrolliert werden.
∕R∞ = 2.28637·10−6. Diese Unterschiede in den
Absorptionswellenlängen durch den Isotopeneffekt werden
in einem neuartigen Verfahren zur Isotropentrennung
(SILEX) verwendet (siehe Mitteilung der DPG
http://www.dpg-physik.de/veroeffentlichung/physik_konkret/pix/Physik_Konkret_11.pdf).
Dieses Verfahren ist ein Hochrisikoverfahren, weil die
notwendigen Apparaturen im Keller eines Einfamilienhauses
Platz haben. So kann die Urananreicherung nicht mehr
kontrolliert werden.
 Lizenzinformationen
Lizenzinformationen