
(Siehe Bronstein, Taschenbuch der Mathematik [BSMM08, pp. 146])
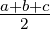
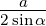 =
= 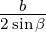 =
= 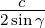
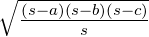 =
s tan
=
s tan 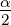 tan
tan 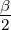 tan
tan 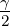 = 4R sin
= 4R sin 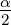
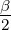
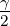
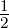 ab sin γ = 2R2 sin α sin β sin γ =
rs =
ab sin γ = 2R2 sin α sin β sin γ =
rs =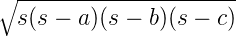
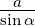 =
= 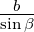 =
= 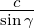 = 2R
= 2R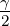 = c cos
= c cos 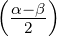
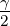 = c sin
= c sin 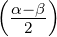
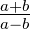 =
= 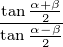
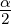 =
= 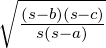
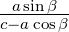 =
= 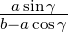
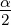 =
= 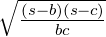
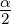 =
= 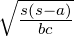
(Siehe Bronstein, Taschenbuch der Mathematik [BSMM08, pp. 148])
___________________________________________________________________________
| gegeben | Formeln | |
| 1. | 1 Seite und 2
Winkel (a,α,β) | γ = π−α−β, b = 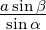 , c = , c = 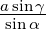 ,
S = ,
S = 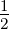 ab sin γ ab sin γ |
| 2. | 2 Seiten und der
eingeschlossene
Winkel (a,b,γ) | tan 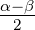 = = 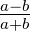 cot cot 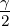 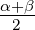 = = 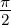 − −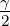 α
und β werden aus α +β und α−β
berechnet. c = α
und β werden aus α +β und α−β
berechnet. c = 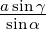 , S = , S = 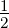 ab sin γ ab sin γ |
| 3. | 2 Seiten und der
einer von ihnen
gegenüberliegende
Winkel (a,b,α) | |
| 4. | 3 Seiten (a,b,c) | r =  , tan , tan 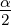 = = 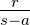 ,
tan ,
tan 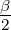 = = 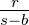 , tan , tan 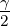 = = 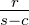 , S = rs = , S = rs =
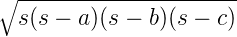 |
_____________________________________________________________________
 Lizenzinformationen
Lizenzinformationen