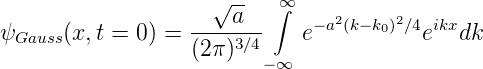

Die Betrachtung im vorherigen Abschnitt legen die Frage nahe: was ist die minimale Grösse des Produktes ΔxΔp? Dazu betrachten wir ein Wellenpaket wie in Abbildung 5.5.1 gezeigt, das durch eine Gausssche Verteilung der Amplitude der Wellenfunktion (im Ortsraum oder in der Zeit) definiert ist.
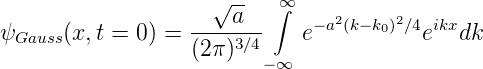 | (5.1) |
Die Vorfaktoren dienen zur Normierung der Funktion. Das Maximum der Wellenfunktion befindet sich bei x = 0 (wie sich herausstellen wird), die Variable a ist die Breite des Pakets und k0 der mittlere Wellenvektor. Die resultierende Funktion ψ(x, 0) ist eine Gausssche Verteilung in Abhängigkeit von x.
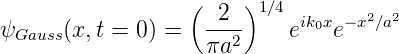 | (5.2) |
Diese Wellenfunktion ist normiert, d.h.
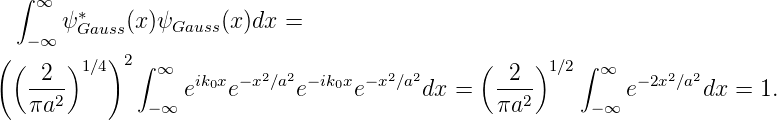 | (5.3) |
Die Streuung von x wird durch 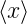 und
und 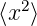 gegeben
gegeben
Die Streuung des Impulses wird mit px = −iℏ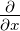 und
px2 = −ℏ2
und
px2 = −ℏ2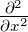 berechnet. Wir berechnen zuerst die erste
Ableitung
berechnet. Wir berechnen zuerst die erste
Ableitung
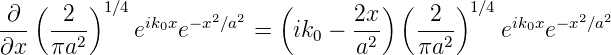 | (5.5) |
und dann die zweite Ableitung
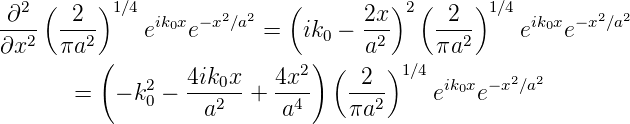 | (5.6) |
Dann ergibt sich
und damit
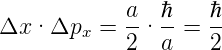 | (5.8) |
Das Gauss’sche Wellenpaket hat, sowohl im Orts- wie auch im Impulsraum, die optimale schmale Ausdehnung. Es ist möglich, auf Kosten der Ortsgenauigkeit die Messgenauigkeit für den Impuls zu steigern, und umgekehrt.
Wir nennen
|
Damit ist gezeigt, dass es unmöglich ist, gleichzeitig Ort und Impuls mit beliebigen Genauigkeit zu messen.
 Lizenzinformationen
Lizenzinformationen