__________________________________________________________________________
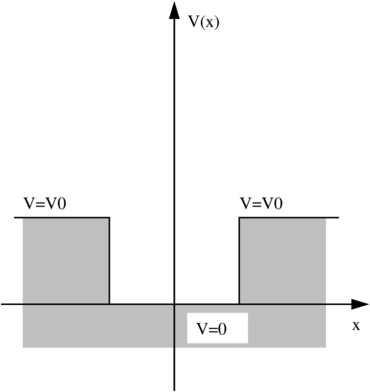
Potentialtopf.
_____________________________________________________________________

__________________________________________________________________________

Potentialtopf.
_____________________________________________________________________
Der Fall eines Teilchens in einem endlichen Potentialtopf ist etwas komplizierter als der Fall des unendlichen. Die Wellenfunktion verschwindet nicht am Rand des Topfes. Wir müssen zwei Fälle betrachten: wenn die Energie höher als die Potentialwälle ist, also E > V 0 und wenn sie kleiner ist. Im ersten Falle haben wir zum Beispiel eine von links einlaufende Welle, die sich an den Diskontinuitäten des Potentials reflektiert. Diese Lösung müsste aus der Lösung des Potentialwalls ablesbar sein. Im zweiten Falle haben wir lokalisierte Wellenfunktionen.
______________________________________________________________________________________________________
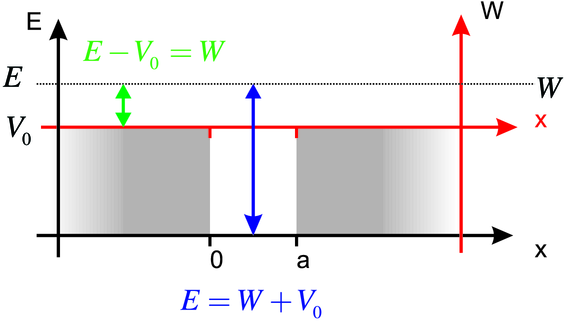
Transformation einer Potentialschwelle in einen Potentialtopf
_____________________________________________________________________
Die Lösungen sind in Gleichung (5.4) angegeben und werden hier nochmals wiederholt.
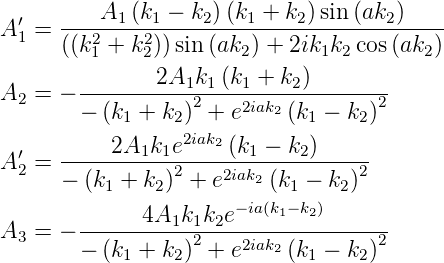
A1 stellt die einfallende Welle dar. der Wert ist frei wählbar. Die Energiewerte müssen aus Gleichung (5.5)
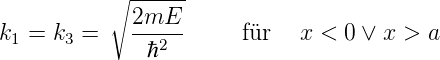 |
und Gleichung (5.6)
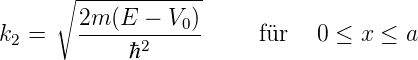 |
werden umskaliert mit E → E − V 0 ausserhalb und E − V 0 → E im Topf. Wir erhalten
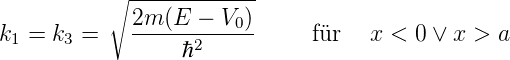 | (5.1) |
und
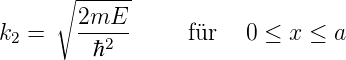 | (5.2) |
Daraus folgen die Transmissions- und Reflexionskoeffizienten T und R
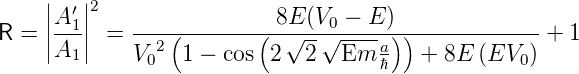 | (5.3) |
und
Die Transmissions- und Reflexionskoeffizienten sind also gleich wie bei einer Barriere, sofern E > V 0 ist. Eine kurze Kontrolle zeigt, dass R + T = 1 ist, wir also keine Teilchen verlieren. Sowohl die Reflexion wie auch die Transmission oszillieren mit der Breite der Barriere a. Die Gleichungen können noch vereinfacht werden:
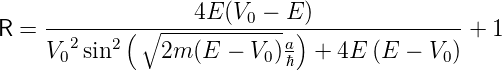 | (5.5) |
und
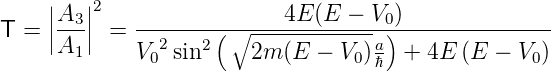 | (5.6) |
__________________________________________________________________________
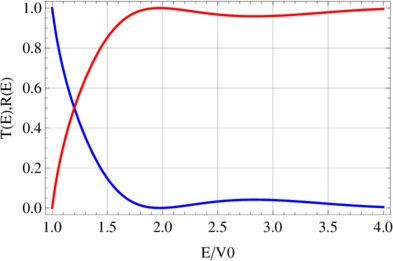
Transmission über einen Potentialtopf.
_____________________________________________________________________
Abbildung 5.11.1 zeigt den Transmissionskoeffizienten und den Reflexionskoeffizienten als Funktion der Energiedifferenz von E zu V 0.
Wenn die Energie des Teilchens E kleiner ist als die potentielle Energie der Wände E < V 0, kann die Schrödingergleichung mit dem allgemeinen Ansatz
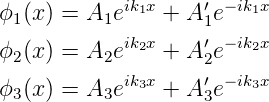 | (5.7) |
gelöst werden. Hier ist k1 = k3. Für x = 0 und x = a sind die Randbedingungen
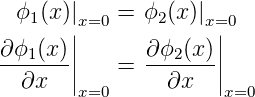 | (5.8) |
sowie
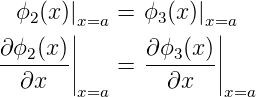 | (5.9) |
Von links und rechts kommen keine Wellen, also ist A1 = A′3 = 0. A2 oder A′2 können frei gewählt werden. Wir lassen A2 als freien Parameter. Dann ist bei x = 0
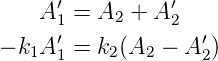 | (5.10) |
und bei x = a
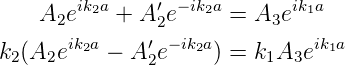 | (5.11) |
Beide Gleichungssysteme können gelöst werden und ergeben eine Beziehung zwischen A′1, A′2 als Funktion von A2 beziehungsweise für A3 und A′2 als Funktion von A2.
Die beiden Lösungen für A′2 müssen identisch sein, das heisst die Gleichung
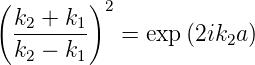 | (5.13) |
muss gelten. Da k2(E) und k1(E,V 0) beides Funktionen von
E sind, ist Gleichung (5.13) eine Bestimmungsgleichung für
die erlaubten Werte von E. Mit k2 = 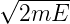 ∕ℏ und
k1 = i
∕ℏ und
k1 = i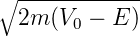 ∕ℏ (da E < V 0 ist) wird Gleichung
(5.13)
∕ℏ (da E < V 0 ist) wird Gleichung
(5.13)
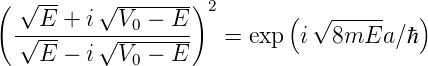 | (5.14) |
Gleichung (5.14) ist nicht analytisch lösbar. Bei den Lösungen muss sowohl der Realteil gleich sein wie auch der Imaginaärteil. Diese sind
Addiert man die quadrierte Gleichung (5.15a) zur
quadrierten Gleichung (5.15b), so erhält man 1 = 1. Es reicht
also, die nummerische Lösung von Gleichung (5.15a) zu
bestimmen. Mit E∕V 0 = x2 und κ(V
0,a) = 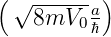 wird
Gleichung (5.15a)
wird
Gleichung (5.15a)
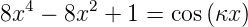 | (5.16) |
Die linke Seite der Gleichung ist invariant. x hat den
Wertebereich [0, 1). Die rechte Seite hängt von a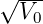 ab.
ab.
__________________________________________________________________________
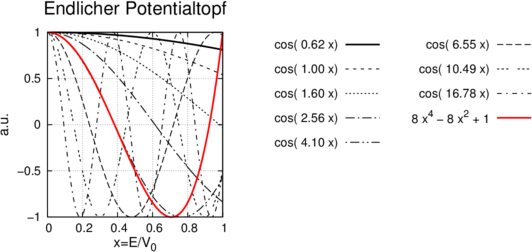
Darstellung von 8x4 − 8x2 + 1 gegen cos(κx) in Abhängigkeit von κ
_______________________________________________________________
Abbildung 5.11.2 zeigt die linke und die rechte Seite der Gleichung 5.16. Die Schnittpunkte mit der roten Linie sind die Lösungen xi. Wenn κ zunimmt, gibt es mehr gebundene Lösungen. Ein zunehmendes κ bedeutet, dass entweder die Potentialtiefe V 0 zugenommen hat, oder aber die Breite des Topfes a.
__________________________________________________________________________
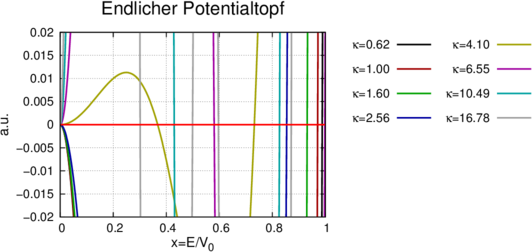
Nullstellen von 8x4 − 8x2 + 1 − cos(κx) = 0 in Abhängigkeit von κ
_______________________________________________________________
Abbildung 5.11.2 zeigt einen vergrösserten Ausschnitt zur Bestimmung der Nullstellen der Gleichung (5.16).
__________________________________________________________________________
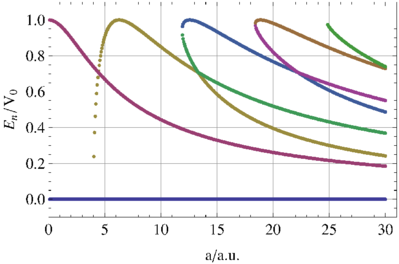
Relative Energieniveaus des Potentialtopfs als Funktion der Topfbreite a.
_____________________________________________________________________
Abbildung 5.11.2 zeigt die Energieniveaus bei konstantem V 0 als Funktion der Topfbreite a. Bei kleinem a existieren nur zwei Niveaus, E0 = 0 und E1 ≈ V 0. Wenn a zunimmt, gibt es mehr Niveaus. Bei a = 4 a.u. sieht man, dass sich zwei Energieniveaus kreuzen. Bei einer vollen Betrachtung würde an dieser Stelle sich eine Bandlücke öffnen.
__________________________________________________________________________
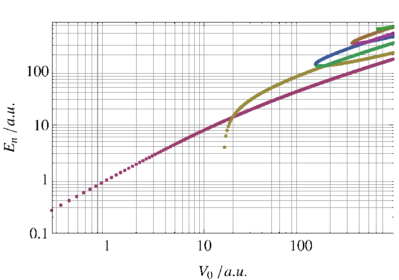
Energieniveaus des Potentialtopfs als Funktion der Wandhöhe V 0.
_____________________________________________________________________
Abbildung 5.11.2 zeigt die Energieniveaus bei konstantem a als Funktion der Wandhöhe V 0. Bei kleinem V 0 existieren nur zwei Niveaus, E0 = 0 (hier nicht angezeigt) und E1 ≈ V 0. Wenn V 0 zunimmt, gibt es mehr Niveaus. Die erste Kreuzung von energieniveaus sieht man bei V 0 = 16 a.u.
 Lizenzinformationen
Lizenzinformationen