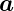 ,
, 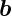 ,
, 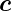 und
und 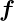 Vektoren oder vektorielle
Funktionen, a, b, c und f ihre Längen, k eine Zahl und φ(
Vektoren oder vektorielle
Funktionen, a, b, c und f ihre Längen, k eine Zahl und φ(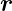 )
eine skalare Funktion. Die Komponenten der Vektoren in
kartesischen Koordinaten sind
)
eine skalare Funktion. Die Komponenten der Vektoren in
kartesischen Koordinaten sind
(Siehe Bronstein, Taschenbuch der Mathematik [Bro+08, pp. 190])
Im Folgenden sind 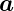 ,
, 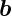 ,
, 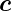 und
und 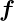 Vektoren oder vektorielle
Funktionen, a, b, c und f ihre Längen, k eine Zahl und φ(
Vektoren oder vektorielle
Funktionen, a, b, c und f ihre Längen, k eine Zahl und φ(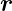 )
eine skalare Funktion. Die Komponenten der Vektoren in
kartesischen Koordinaten sind
)
eine skalare Funktion. Die Komponenten der Vektoren in
kartesischen Koordinaten sind
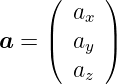 |
Für die anderen Vektoren werden die Komponenten analog geschrieben.
Skalarprodukt
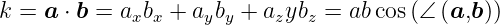 | (D.1) |
Vektorprodukt
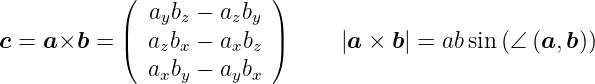 | (D.2) |
Vertauschung der Reihenfolge (Kommutationsgesetze)
Zwei Vektoren sind orthogonal, wenn
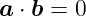 | (D.5) |
Sie sind kollinear, wenn
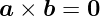 | (D.6) |
Doppeltes Vektorprodukt
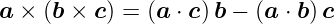 | (D.7) |
Spatprodukt oder gemischtes Produkt
Drei Vektoren sind komplanar, wenn
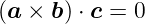 | (D.9) |
Lagrangesche Identität
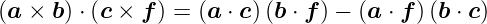 | (D.10) |
Vierfaches Vektorprodukt
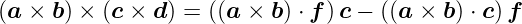 | (D.11) |
Ableiten eines Vektors
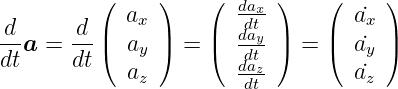 | (D.12) |
Ableitung eines Produktes
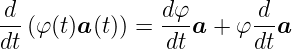 | (D.13) |
Ableitung des Skalarproduktes
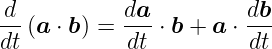 | (D.14) |
Ableitung des Vektorproduktes
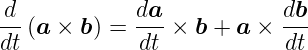 | (D.15) |
Ableitung eines Vektors mit konstantem Betrag. Hier ist
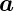 ⋅
⋅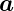 = a2 = const. Aus Gleichung (D.14) folgt
= a2 = const. Aus Gleichung (D.14) folgt
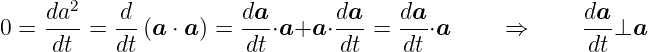 | (D.16) |
Taylorentwicklung einer Vektorfunktion
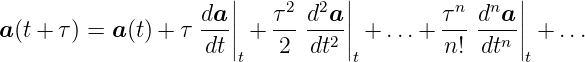 | (D.17) |
Ableitung eines skalaren Feldes nach einer Richtung
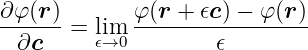 | (D.18) |
Ableitung 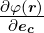 in Richtung des Einheitsvektors
in Richtung des Einheitsvektors 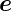
 in
Richtung von
in
Richtung von 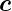
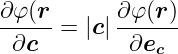 | (D.19) |
Richtungsableitung einer skalaren Funktion im Vergleich
zur Richtung mit dem stärksten Abfall (Einheitsvektor
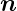 )
)
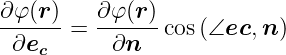 | (D.20) |
Ableitung eines Vektorfeldes 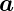 nach einer Richtung
nach einer Richtung
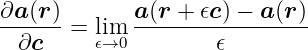 | (D.21) |
Ableitung 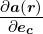 in Richtung des Einheitsvektors
in Richtung des Einheitsvektors 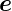
 in
Richtung von
in
Richtung von 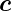
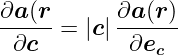 | (D.22) |
Richtungsableitung einer Vektorfunktion
Gradient eines Produktes
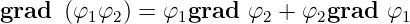 | (D.24) |
Kettenregel beim Gradienten
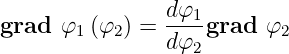 | (D.25) |
Gradient eines Skalarproduktes
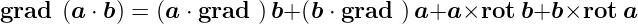 | (D.26) |
Gradient eines Skalarproduktes eines konstanten Vektors 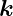 mit einem Ortsvektor
mit einem Ortsvektor 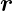
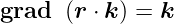 | (D.27) |
Divergenz eines Produktes
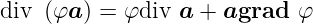 | (D.28) |
Divergenz eines Skalarproduktes eines konstanten Vektors 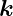 mit einem Ortsvektor
mit einem Ortsvektor 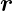
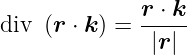 | (D.29) |
Divergenz eines Vektorproduktes
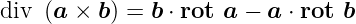 | (D.30) |
Rotation eines Produktes
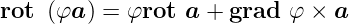 | (D.31) |
Divergenz eines Vektorproduktes
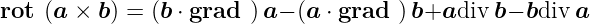 | (D.32) |
Rotation eines Potentialfeldes
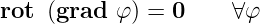 | (D.33) |
Divergenz einer Rotation
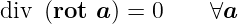 | (D.34) |
Rotation einer Rotation
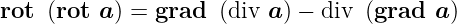 | (D.35) |