Weiter: Hall-Effekt Oben: Elektrische Ströme Zurück: Die magnetische Kraft Skript: PDF-Datei Übungen: Blätter
(Siehe Leisi, Klassische Physik II [Lei98, pp. 98])
|
|
Um nicht immer die Lorentz-Transformation ausrechnen zu müssen , führen wir die magnetische
Feldstärke oder die magnetische Induktion
![]() ein. Ein magnetisches Feld lenkt Elektronen ab. Wie wir schon früher gesehen haben, ist eine Bewegung
der Ladungsträger für die magnetische Kraft notwendig. Wird das Magnetfeld der Helmholtzspulen so
gedreht, dass es parallel zur Bewegungsrichtung der Elektronen liegt, verschwindet die Magnetkraft. Das
folgende Kraftgesetz
ein. Ein magnetisches Feld lenkt Elektronen ab. Wie wir schon früher gesehen haben, ist eine Bewegung
der Ladungsträger für die magnetische Kraft notwendig. Wird das Magnetfeld der Helmholtzspulen so
gedreht, dass es parallel zur Bewegungsrichtung der Elektronen liegt, verschwindet die Magnetkraft. Das
folgende Kraftgesetz
beschreibt die magnetischen Kräfte auf Elektronen. Die Kraft ![]() heisst Lorentz-Kraft.
heisst Lorentz-Kraft.
Durch den Vergleich von Gleichung (3.104) und Gleichung (3.101) kann man für die magnetische Feldstärke einer linienförmigen Stromverteilung schreiben
![\includegraphics[width=0.7\textwidth]{strom-006}](img864.gif)
|
|
|
Materialien
Folien zur Vorlesung vom 05. 06. 2008: PDF Seminar vom 05. 06. 2008. Aufgabenblatt 08 |
|
Die magnetische Induktion |
|
|
| Die magnetische Induktion eines geraden, unendlich ausgedehnten Stromes bildet Feldlinien, die kreisförmig in einer Ebene senkrecht zum Strom liegen. Der Mittelpunkt der kreisförmigen Feldlinien ist der Strom. |
Die Kraft zwischen zwei stromdurchflossenen Leitern kann neu berechnet werden. Mit
| (3.253) |
| (3.254) |
| (3.255) |
|
Die Einheit der magnetischen Induktion ist
![$\displaystyle [B] = Tesla = T = \frac{N\cdot s}{C \cdot m} = \frac{N}{A m}= \frac{V\cdot s}{m^2}$](img875.gif) |
(3.259) |
Die magnetische Induktion wurde so definiert, dass in Gleichung (3.112) alle Faktoren bis auf den Strom ![]() und die
Länge
und die
Länge ![]() durch
durch ![]() symbolisiert werden. Diese Wahl ist willkürlich. Wir hätten genau so gut ein Feld
durch
symbolisiert werden. Diese Wahl ist willkürlich. Wir hätten genau so gut ein Feld
durch
![$\displaystyle \left[H\right] = \frac{A}{m}$](img879.gif)
Das magnetische Feld
|
Die Kraft auf einen stromdurchflossenen Leiter in einem beliebigen Magnetfeld kann mit dem Gesetz von Biot-Savart berechnet werden.
![\includegraphics[width=0.7\textwidth]{strom-007}](img887.gif)
Berechnung der Kraft auf ein Leiterelement.
|
Der Betrag des Vektors ![]() , der senkrecht auf
, der senkrecht auf
![]() und senkrecht auf
und senkrecht auf ![]() steht, ist
steht, ist
| (3.262) |
| (3.263) |
Beispiel:
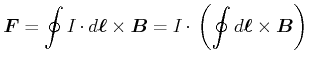 |
(3.265) |
|
|
|
|
![\includegraphics[width=0.7\textwidth]{strom-008}](img899.gif)
Drehmoment auf eine Leiterschleife im homogenen Magnetfeld
|
Bezüglich 0 ist die Situation symmetrisch. Die in der Zeichnung vertikalen Leiterelemente
liefern kollineare sich aufhebende Kräfte. Die horizontalen Segmente ergeben das infinitesimale Drehmoment
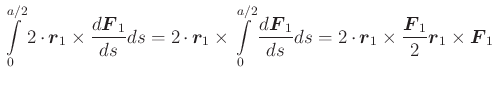 entsprechend für die untere Seite), ist
entsprechend für die untere Seite), ist
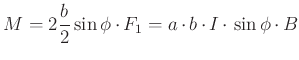 |
(3.267) |
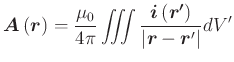 |
(3.269) |
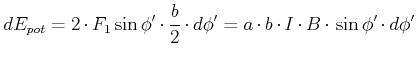 |
(3.270) |
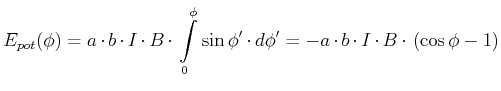 |
(3.271) |
| (3.272) |
Ein weiteres Beispiel einer Kraftwirkung auf Ladungen ist das Barlowsche Rad.
|
|
(Siehe Leisi, Klassische Physik II [Lei98, pp. 104])
Beim unendlich ausgedehnten geraden Leiter war das durch einen Strom ![]() erzeugte Magnetfeld durch kreisförmige
Magnetfeldlinien mit der Stärke
erzeugte Magnetfeld durch kreisförmige
Magnetfeldlinien mit der Stärke
![]() charakterisiert, wobei das
charakterisiert, wobei das ![]() -Feld tangential
zu den Kreisen liegt. Das Linienintegral entlang der Feldlinien, also entlang des Kreises
-Feld tangential
zu den Kreisen liegt. Das Linienintegral entlang der Feldlinien, also entlang des Kreises ![]() , ergibt
, ergibt
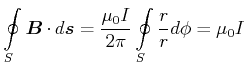 |
(3.273) |
Der Beweis geht in mehreren Schritten:
![\includegraphics[width=0.5\textwidth]{strom-009}](img926.gif)
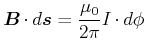
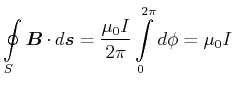
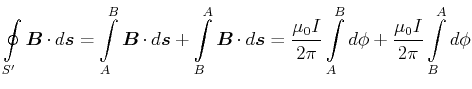
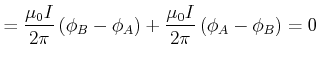
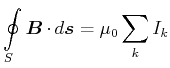
Beispiel:
Ein zylindrischer Leiter mit dem Radius ![]() soll homogen vom Strom
soll homogen vom Strom ![]() durchflossen werden. Die
Stromdichte
durchflossen werden. Die
Stromdichte ![]() und der Strom
und der Strom ![]() stehen dann betragsmässig wie
stehen dann betragsmässig wie
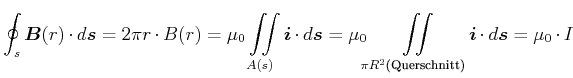
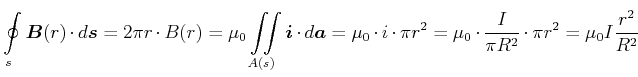
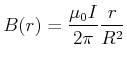
![\includegraphics[width=0.6\textwidth]{B_linienstrom}](img944.gif)
Tangentiales Magnetfeld eines ausgedehnten, unendlich langen Linienstromes.
|
Mit dem Stokeschen Satz (Gleichung (C.43) ) kann man die Integralform des Ampèreschen Gesetzes umschreiben
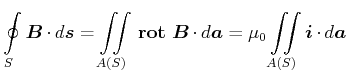 |
(3.275) |
|
|
Materialien
Folien zur Vorlesung vom 09. 06. 2008: PDF |
Beispiel: homogene Stromverteilung in einem unendlich ausgedehnten Leiter
Wir definieren eine lineare Stromdichte
![]() . Das Stromfeld können wir uns als Parallelschaltung vieler linearer Leiter vorstellen. Aus dem
Superpositionsprinzip folgt, dass in der
. Das Stromfeld können wir uns als Parallelschaltung vieler linearer Leiter vorstellen. Aus dem
Superpositionsprinzip folgt, dass in der ![]() -Richtung
-Richtung
| (3.277) |
Wir betrachten weiter die Komponenten ![]() und
und ![]() des Feldes
des Feldes ![]() im Abstand
im Abstand ![]() von der
Platte. Wir werden zwei Symmetrieoperationen an:
von der
Platte. Wir werden zwei Symmetrieoperationen an:
| (3.278) |
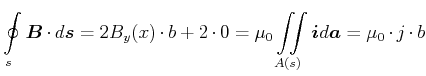
Das Resultat ist unabhängig von ![]() und homogen im Raum. Die Magnetfeldlinien sind parallel zur Platte und links
und rechts antiparallel (siehe Abbildung 3.32, Mitte).
und homogen im Raum. Die Magnetfeldlinien sind parallel zur Platte und links
und rechts antiparallel (siehe Abbildung 3.32, Mitte).
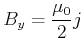 |
(3.279) |
| (3.280) |
(Siehe Leisi, Klassische Physik II [Lei98, pp. 111])
In diesem Abschnitt soll gezeigt werden, dass das Magnetfeld quellenfrei ist.
![\includegraphics[width=0.4\textwidth]{strom-010}](img963.gif)
Integrationsfläche zur Analyse der Quellenfreiheit des Magnetfeldes
|
Da überall auf der Integrationsfläche ![]() gilt:
gilt:
![]() , ist
, ist
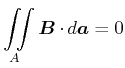 |
(3.281) |
Wir verallgemeinern das Resultat, indem wir einen Zylinder mit beliebiger Grund- und Deckfläche nehmen. Auf der Grund und Deckfläche gilt das vorherige Argument, so dass
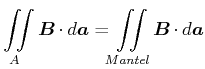
ist.
![\includegraphics[width=0.5\textwidth]{strom-011}](img967.gif)
Integration über die Mantelfläche.
|
An der Mantelfläche gilt mit
![]()
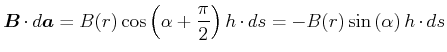
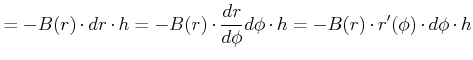
und damit
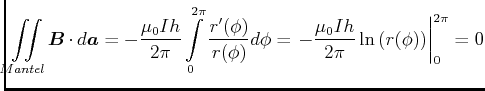
Damit gilt auch für allgemeine Zylinderflächen
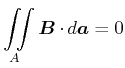 |
(3.282) |
Die Quellenfreiheit des magnetischen Feldes bedeutet, dass es keine magnetischen Ladungen gibt und dass die Feldlinien im Endlichen geschlossen sind.
(Siehe Leisi, Klassische Physik II [Lei98, pp. 114])
|
|
In diesem Abschnitt wollen wir die Frage lösen: wie konstruiere ich eine magnetische Induktion ![]() möglichst bequem? Das Rezept stammt aus der Elektrizitätslehre (Siehe Abschnitt 2.5). Dort
wurde gezeigt, dass aus einem beliebigen Potential
möglichst bequem? Das Rezept stammt aus der Elektrizitätslehre (Siehe Abschnitt 2.5). Dort
wurde gezeigt, dass aus einem beliebigen Potential
![]() durch
durch
| (3.285) |
werden beide Gleichungen erfüllt. Wegen der Vektoridentität
| (3.286) |
| (3.287) |
Das Vektorpotential ![]() kann immer so gewählt werden, dass
kann immer so gewählt werden, dass
![]() gilt.
gilt.
Das Vektorpotential ist nicht eindeutig bestimmt. Nehmen wir an, dass ein Vektorpotential mit
![]() existiert. Dann existiert auch ein Vektorfeld
existiert. Dann existiert auch ein Vektorfeld
![]() mit
mit
|
Das zu einer realen physikalischen Situation gehörende Vektorpotential |
| In der Relativitätstheorie und in der Quantenmechanik rechnet man bevorzugt mit dem Vektorpotential. |
Aus der Gleichung für das Vektorpotential einer Stromverteilung
Aus der Beziehung
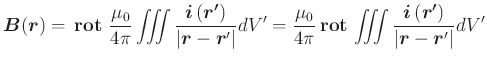 (Siehe Landau und Lifschitz, Klassische Feldtheorie [, pp. 121]) bekommen wir
(Siehe Landau und Lifschitz, Klassische Feldtheorie [, pp. 121]) bekommen wir
Nun bezieht sich die Rotation nur auf ![]() , nicht aber auf
, nicht aber auf ![]() . Deshalb kann sie unter das Integral gezogen werden.
. Deshalb kann sie unter das Integral gezogen werden.
Nun gilt für die Rotation eines Produktes (Siehe Bronstein, Taschenbuch der Mathematik [BSMM00, pp. 468])
Hier ist der Vektor
![]() bezüglich der Rotation eine Konstante, da er nur von
bezüglich der Rotation eine Konstante, da er nur von ![]() und nicht von
und nicht von ![]() abhängt. Weiter darf die Ableitung irgend eines Punktes nicht davon abhängen dass das Koordinatensystem um einen Konstanten Vektor verschoben wurde. Wir rechnen deshalb die Ableitungen in der Rotation, beziehungsweise im Gradienten, nicht bezüglich
abhängt. Weiter darf die Ableitung irgend eines Punktes nicht davon abhängen dass das Koordinatensystem um einen Konstanten Vektor verschoben wurde. Wir rechnen deshalb die Ableitungen in der Rotation, beziehungsweise im Gradienten, nicht bezüglich ![]() sondern bezüglich des verschobenen Koordinatensystems
sondern bezüglich des verschobenen Koordinatensystems
![]() aus. Es bleibt also
aus. Es bleibt also
Wir betrachten nun einen infinitesimal dünnen Strom
![]() .
.
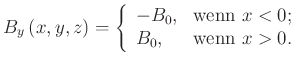 ist ein Einheitsvektor entlang des Drahtes. Da
ist ein Einheitsvektor entlang des Drahtes. Da ![]() überall null ist ausser auf dem eindimensionalen Draht, wird aus dem Volumenintegral ein eindimensionales Integral. Wieder ist es für die Integration egal, ob wir
überall null ist ausser auf dem eindimensionalen Draht, wird aus dem Volumenintegral ein eindimensionales Integral. Wieder ist es für die Integration egal, ob wir ![]() von
von ![]() oder von
oder von
![]() abhängen lassen.
abhängen lassen.
Diese Gleichung ist bekannt als das Gesetz von Biot-Savart. Mit ihm kann man das Feld einer beliebigen Leiteranordnung berechnen.
Auch wenn sie physikalisch keine Bedeutung hat, kann es sinnvoll sein in Zwischenschritten die differentielle Formulierung zu verwenden, nämlich die Formel von Laplace.
Beispiel:
Wir hatten in Abbildung 3.32 gesehen, dass ein homogener Strom in die ![]() -Richtung homogene
magnetische Induktionen links und rechts erzeugt. Die Magnetfelder haben die Form
-Richtung homogene
magnetische Induktionen links und rechts erzeugt. Die Magnetfelder haben die Form
Für ![]() ist
ist ![]() nicht definiert.
nicht definiert.
![\includegraphics[width=0.7\textwidth]{strom-051}](img1023.gif)
Darstellung von
|
Das zu Gleichung (3.151) gehörige Vektorpotential ist
![\includegraphics[width=0.7\textwidth]{strom-050}](img1037.gif)
|
Beispiel:
Das Vektorpotential
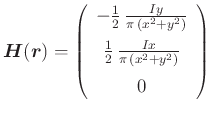
ergibt das magnetische Feld für einen in der ![]() -Richtung laufenden Strom
-Richtung laufenden Strom ![]()
In Zylinderkoordinaten
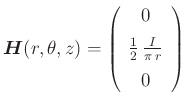 gehört zum Magnetfeld
gehört zum Magnetfeld
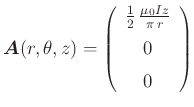
das Vektorpotential
Othmar Marti