__________________________________________________________________________
Berechnung der Energie im Magnetfeld
_____________________________________________________________________

__________________________________________________________________________

Berechnung der Energie im Magnetfeld
_____________________________________________________________________
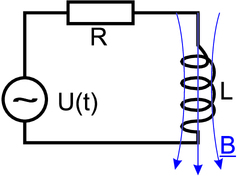
Wir betrachten eine mit einer Wechselstromquelle U(t) = U0 sin(ωt) verbundene reale Spule. Diese Spule wird modelliert durch einen Widerstand R und eine ideale Spule L. Die Differentialgleichung dieses Kreises lautet
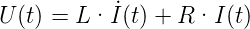 | (4.1) |
Die stationäre Lösung dieser Gleichung hat die Form
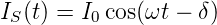 | (4.2) |
Für den Fall, dass R « ωL ist, bekommt man
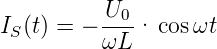 | (4.3) |
Die momentane Leistung der Spannungsquelle ist
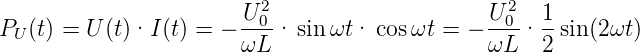 | (4.4) |
Die Leistung der Spannungsquelle kann nur die Energie des
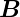 -Feldes ändern, da wir keine dissipativen Elemente haben
(R = 0). Wenn man die Differentialgleichung für den Fall mit
I(t) multipliziert, bekommt man
-Feldes ändern, da wir keine dissipativen Elemente haben
(R = 0). Wenn man die Differentialgleichung für den Fall mit
I(t) multipliziert, bekommt man
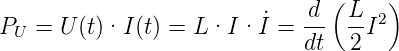 | (4.5) |
Nun ist aber P = dE∕dt. Damit ist die Energie des Magnetfeldes
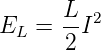 | (4.6) |
Um die Energiedichte eines Magnetfeldes zu berechnen betrachten wir eine Spule
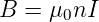 | (4.7) |
mit der Selbstinduktivität
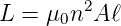 | (4.8) |
wobei A der Querschnitt der Spule und ℓ ihre Länge ist. Eingesetzt in die Gleichung für die Energie EL bekommt man
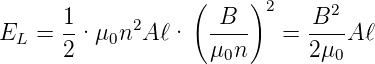 | (4.9) |
Deshalb ist die Energiedichte des 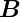 -Feldes
-Feldes
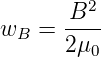 | (4.10) |
 Lizenzinformationen
Lizenzinformationen