Weiter: Zentralbewegung Oben: Mechanik Zurück: Teilchensysteme Skript: PDF-Datei Übungen: Blätter
|
|
Stösse sind kurzzeitige Wechselwirkungen (WW) zwischen zwei Körpern.
|
Stoss zweier Massen
|
Impulserhaltung (eindimensionales Problem, also kann man mit Zahlen rechnen)
Stösse heissen elastisch wenn gilt
Dann kann aus Gleichung (3.162) und Gleichung (3.163) ![]() und
und ![]() ausgerechnet werden.
ausgerechnet werden.
Wir schreiben die Gleichungen um und erhalten
| (3.206) |
und
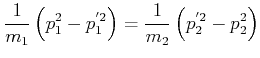 |
Ausmultipliziert bekommen wir
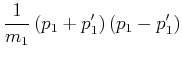 |
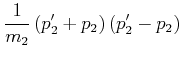 |
(3.207) | |
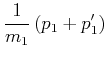 |
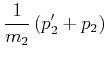 |
(3.208) |
| (3.209) |
Also ist die Relativgeschwindigkeit nach dem Stoss (
![]() ) das Negative der Relativgeschwindigkeit vor
dem Stoss (
) das Negative der Relativgeschwindigkeit vor
dem Stoss (
![]() ).
).
Das bedeutet, dass bei einer Frontalkollision von einem Auto (
![]() ) mit einem Fussgänger (
) mit einem Fussgänger (
![]() ) die Relativgeschwindigkeit vorher
(
) die Relativgeschwindigkeit vorher
(
![]() ) gleich dem negativen der Relativgeschwindigkeit nach dem Stoss ist. Da das Auto aber (siehe
unten) nur unwesentlich abgebremst wird, fliegt der Fussgänger nach dem Stoss mit
) gleich dem negativen der Relativgeschwindigkeit nach dem Stoss ist. Da das Auto aber (siehe
unten) nur unwesentlich abgebremst wird, fliegt der Fussgänger nach dem Stoss mit
![]() durch
die Gegend.
durch
die Gegend.
Die Impulse nach dem Stoss sind dann
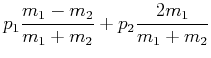 |
(3.210) | ||
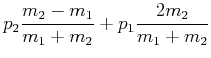 |
(3.211) |
Es gibt die folgenden Spezialfälle:
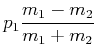 |
(3.212) | ||
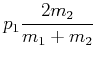 |
(3.213) |
| (3.214) | |||
| (3.215) |
| (3.216) | |||
| (3.217) |
Wir nennen einen Stoss vollkommen plastisch, wenn die beiden Körper nach dem Stoss aneinander kleben, wenn sie
quasi zu einer Masse (
![]() ) mit einer Geschwindigkeit (
) mit einer Geschwindigkeit (
![]() ) geworden
sind. Dann ist
) geworden
sind. Dann ist
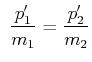 |
(3.218) |
Die Impulserhaltung ergibt dann
| (3.219) | |||
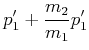 |
(3.220) | ||
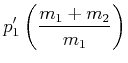 |
(3.221) | ||
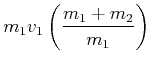 |
(3.222) | ||
| (3.223) | |||
| (3.224) |
und damit für die Teilimpulse
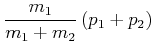 |
(3.225) | ||
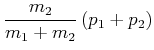 |
(3.226) |
Beim plastischen Stoss ist die Energie nicht erhalten. Wir bezeichnen mit ![]() die Energie, die in Wärme und
Deformation gespeichert wird.
die Energie, die in Wärme und
Deformation gespeichert wird.
| (3.227) | |||
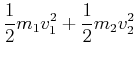 |
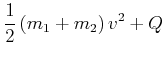 |
(3.228) |
Für die Endgeschwindigkeit hatten wir
![]() und damit
und damit
![]() . Eingesetzt
. Eingesetzt
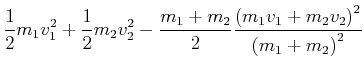 |
(3.229) | ||
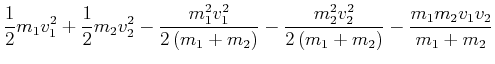 |
(3.230) | ||
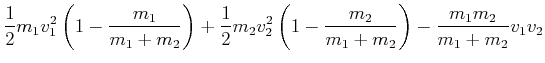 |
(3.231) | ||
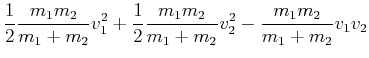 |
(3.232) | ||
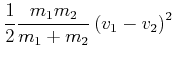 |
(3.233) |
Die Grösse
![]() heisst auch die
reduzierte Masse. Mit ihr können Zweikörper-Probleme
im Schwerpunktssystem einfacher gelöst werden.
heisst auch die
reduzierte Masse. Mit ihr können Zweikörper-Probleme
im Schwerpunktssystem einfacher gelöst werden.
|
|
Als Annäherung an den dreidimensionalen Fall betrachten wir den elastischen Stoss in der Ebene. Jeder Stoss im Raum mit zwei Körpern kann auf den ebenen Fall zurückgeführt werden (warum?).
![\includegraphics[width=0.7\textwidth]{mechanik-046}](img950.gif)
Stoss in einer Ebene
|
Annahmen
| (3.234) | |||
| (3.235) |
Impulssatz:
| (3.236) | |||
| (3.237) |
Energiesatz:
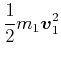 |
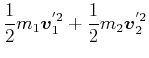 |
(3.238) | |
| (3.239) |
Zusammengesetzt erhalten wir
| (3.240) | |||
| (3.241) |
oder
| (3.242) |
Da das Skalarprodukt zweier Vektoren null ist, ist der Zwischenwinkel bei jedem elastischen ebenen Stoss (und damit bei jedem elastischen Stoss)
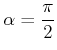 |
(3.243) |
Wir betrachten Stösse, bei denen der zweite Stosspartner ruht. Die Geschwindigkeit des ersten
Stosspartners (![]() ) definiert eine Richtung. Der Abstand des Strahls definiert durch
) definiert eine Richtung. Der Abstand des Strahls definiert durch
![]() von
der Masse
von
der Masse
![]() wird mit
wird mit ![]() (Stossparameter) bezeichnet.
(Stossparameter) bezeichnet.
![\includegraphics[width=0.7\textwidth]{mechanik-047}](img970.gif)
Definition des Stossparameters
|
nach dem Stoss:
![\includegraphics[width=0.4\textwidth]{mechanik-048}](img971.gif)
Situation nach einem ebenen Stoss
|
Unbekannte sind
![]()
Impulserhaltung: in der ![]() -Richtung
-Richtung
| (3.244) |
Impulserhaltung in der ![]() -Richtung
-Richtung
| (3.245) |
Energieerhaltung
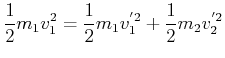 |
(3.246) |
Eine 4. Relation ist durch den Stossparameter ![]() und die Physik der Wechselwirkung gegeben.
und die Physik der Wechselwirkung gegeben.
Experimentelle Stossverteilungen werden mit ![]() parametrisiert.
parametrisiert.
Grundlage: 2.Newton'sches Gesetz
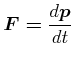 |
(3.247) |
|
|
![\includegraphics[width=0.5\textwidth]{mechanik-049}](img977.gif)
Rückstoss bei einer Armbrust
|
Länge:![]() (für Beschleunigung Beschleunigungsstrecke)
(für Beschleunigung Beschleunigungsstrecke)
Endgeschwindigkeit: ![]()
Antriebszeit:![]()
Rückstosskraft: ![]()
Wir erhalten die Betragsgleichung
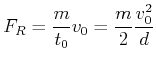 |
(3.248) |
Beweis: Antrieb:
![]()
Newton:
![]()
Wenn
![]() über die Beschleunigungsphase konstant ist, gilt:
über die Beschleunigungsphase konstant ist, gilt:
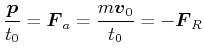 |
(3.249) |
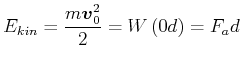 |
(3.250) |
|
|
![\includegraphics[width=0.8\textwidth]{mechanik-050}](img987.gif)
Kräfte an einer Raketendüse. Die Rakete ist fixiert.
|
Die Masse des wegfliegenden Gases trägt einen mit der Zeit grösser werdenden Impuls. Dieser Impulsänderung
entspricht eine äussere Kraft ![]() und einer Schubkraft
und einer Schubkraft
![]() . Wir beachten weiter, dass
wir Vektoren mit den dem Koordinatensystem angepassten Komponenten verwenden müssen. Hier hat also
. Wir beachten weiter, dass
wir Vektoren mit den dem Koordinatensystem angepassten Komponenten verwenden müssen. Hier hat also
![]() eine negative
eine negative ![]() -Komponente.
-Komponente.
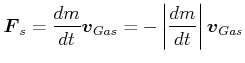 |
(3.251) |
wobei mit
![]() die Relativgeschwindigkeit zur Düse gemeint ist.
die Relativgeschwindigkeit zur Düse gemeint ist.
Beweis mit Newton
| (3.252) | |||
| (3.253) | |||
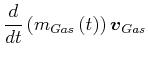 |
(3.254) | ||
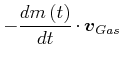 |
(3.255) |
![\includegraphics[width=0.7\textwidth]{mechanik-051}](img997.gif)
Kräfte an einer Rakete
|
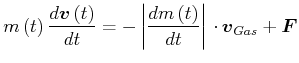 |
(3.256) |
Beweis:
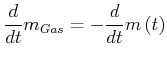 |
(3.257) |
Wenn ein Massenelement ![]() die Düse verlässt, hat es in diesem Augenblick die
Geschwindigkeit
die Düse verlässt, hat es in diesem Augenblick die
Geschwindigkeit
![]() . Es trägt also den Impuls
. Es trägt also den Impuls
![]() weg. Auch hier verwenden wir die
Vektoren mit den durch das Koordinatensystem gegebenen richtigen Vorzeichen.
Infinitesimal gilt
weg. Auch hier verwenden wir die
Vektoren mit den durch das Koordinatensystem gegebenen richtigen Vorzeichen.
Infinitesimal gilt
und damit
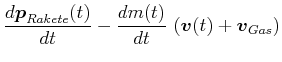 |
(3.258) | ||
![$\displaystyle \left\{ m\left( t\right) \frac{d\vec{v}\left( t\right) }{dt}+\fra...
...right) }{dt}\left[ \vec{v}\left( t\right) +\vec{v}_{Gas}\right]
\right\} \notag$](img1006.gif) |
(3.259) | ||
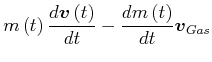 |
(3.260) |
Bewegung der kräftefreien Rakete:
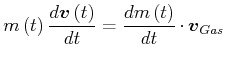 |
(3.261) |
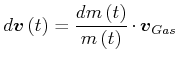 |
(3.262) |
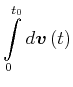 |
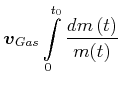 |
(3.263) | |
| (3.264) | |||
| (3.265) |
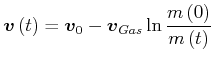 |
(3.266) |
das heisst, die Endgeschwindigkeit einer Rakete kann man steigern, indem man die Ausströmgeschwindigkeit des Gases
![]() erhöht, oder indem man die Endmasse
erhöht, oder indem man die Endmasse
![]() im Vergleich zur Anfangsmasse
im Vergleich zur Anfangsmasse
![]() möglichst klein macht. Die zweite Lösung ergibt aber strukturelle Probleme
möglichst klein macht. Die zweite Lösung ergibt aber strukturelle Probleme
Othmar Marti