Da jede Huygenssche Elementarwelle eine periodische Schwingung mit einer gegebenen Frequenz ![]() darstellt, ändert sich die Frequenz beim Übergang von einem Medium in das zweite nicht. Da die
Ausbreitungsgeschwindigkeit
darstellt, ändert sich die Frequenz beim Übergang von einem Medium in das zweite nicht. Da die
Ausbreitungsgeschwindigkeit ![]() kleiner ist, gilt für die Wellenlänge
kleiner ist, gilt für die Wellenlänge
| (3.5) |
In einem Medium mit einer Brechzahl ![]() ist die Wellenlänge kleiner. So hat rotes Licht
ist die Wellenlänge kleiner. So hat rotes Licht
![]() in Glas die Wellenlänge
in Glas die Wellenlänge
![]() .
.
![\includegraphics[width=0.6\textwidth]{brechung-geometrie.eps}](img81.gif)
Geometrie der Brechung
|
Wir betrachten nun den Weg, den das Licht im Inneren eines Mediums zurücklegt. Wir berücksichtigen, dass die
Geschwindigkeit im Medium um den Brechungsindex ![]() kleiner ist. Aus dem rechtwinkligen Dreieck
wissen wir, dass
kleiner ist. Aus dem rechtwinkligen Dreieck
wissen wir, dass
| (3.6) |
| (3.7) |
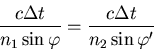 |
(3.8) |
![\framebox[0.9\textwidth]{\begin{minipage}{0.9\textwidth}\large\textcolor{red}{Br...
...quation}
n_1 \sin\varphi _1 = n_2 \sin\varphi _2
\end{equation}}\end{minipage}}](img93.gif)
Materialien
Folien zur Vorlesung am 24. 04. 2002 (PDF)
Bei diesem Gesetz gibt es nur dann immer eine Lösung, wenn ![]() ist. Sonst gibt es den Winkel der
Totalreflexion. Wenn der vom optisch dichteren Medium einfallende Lichtstrahl gegen die
Grenzflächennormale den Winkel
ist. Sonst gibt es den Winkel der
Totalreflexion. Wenn der vom optisch dichteren Medium einfallende Lichtstrahl gegen die
Grenzflächennormale den Winkel
![]() hat und der Winkel des resultierenden Lichtstrahls gegen die
Grenzflächennormale im optisch dünneren Medium
hat und der Winkel des resultierenden Lichtstrahls gegen die
Grenzflächennormale im optisch dünneren Medium ![]() ist, hat das Brechungsgesetz gerade noch eine reelle
Lösung.
ist, hat das Brechungsgesetz gerade noch eine reelle
Lösung.
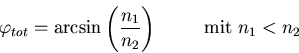 |
(3.9) |
Für Winkel, die grösser als
![]() sind, wird Licht aus dem optisch dünneren Medium total reflektiert.
Die Reflexion geschieht in einer Tiefe von etwa
sind, wird Licht aus dem optisch dünneren Medium total reflektiert.
Die Reflexion geschieht in einer Tiefe von etwa ![]() innerhalb des optisch dünneren Mediums.
innerhalb des optisch dünneren Mediums.
![\includegraphics[width=0.6\textwidth]{reflexion-glasfaser.eps}](img100.gif)
Transport von Licht in einer Stufenindexfaser
|
Wenn Licht mit einem Winkel nahe der Achse der optischen Faser in diese eingekoppelt wird, dann wird das Licht mit Totalreflexion transportiert. Nur Licht, das innerhalb des Akzeptanzwinkels den Faserkern trifft, wird weitertransportiert. Wenn die faser gekrümmt wird, dann verlässt ein Teil des Lichtes die Faser: Krümmungen in der Faser erhöhen die Verluste.
Wenn der Faserkern den Durchmesser ![]() hat, ist der effektive Weg vom Winkel
hat, ist der effektive Weg vom Winkel ![]() gegen die Achse
abhängig. Die Hypothenuse ist
gegen die Achse
abhängig. Die Hypothenuse ist
![]() lang, der direkte Weg wäre
lang, der direkte Weg wäre
![]() . Die
relative Längenänderung ist
. Die
relative Längenänderung ist
| (3.10) |
| (3.11) |
| (3.12) |
Im allgemeinen Falle hängt die Phasengeschwindigkeit einer Welle von der Frequenz und vom Medium ab. Das heisst für Licht, dass jede Farbe eine eigene Ausbreitungsgeschwindigkeit hat.
![\includegraphics[width=0.53\textwidth]{prisma.eps}](img109.gif)
![\includegraphics[width=0.4\textwidth]{dispersion-kurve.eps}](img110.gif)
Links: Strahlengang durch ein Prisma. Rechts: Dispersion einiger Materialien
|
Durch die Dispersion des Lichtes, das heisst, dass die Brechzahl von der Wellenlänge abhängt, werden die verschiedenen Farben unterschiedlich gebrochen. Jedesmal, wenn Licht durch die Grenzfläche Luft-Materie geht, werden unterschiedliche Farben unterschiedlich gebrochen. Dies bewirkt die folgenden Effekte:
![\includegraphics[width=0.8\textwidth]{dispersion-federmodell.eps}](img111.gif)
Federmodell für die Dispersion nach (Siehe Känzig, Mechanik und Wellenlehre[Kän78, 292]) .
|
Wir betrachten eine longitudinale Welle auf einem Feder-Masse-System. Die Bewegungsgleichung für die n-te
Masse ist
| (3.13) |
![\begin{displaymath}
\ddot\xi_n =
\Omega_0^2\left[\frac{1}{4}\left(\xi_{n+1}+\xi_{n-1}\right)-\frac{1}{2}\xi_n\right]
\end{displaymath}](img116.gif) |
(3.14) |
| (3.15) |
![$\displaystyle \Omega_0^2\left[\frac{1}{4}\left(e^{ik(n-1)a} + e^{ik(n+1)a}\right)
-\frac{1}{2}e^{ikna}\right]$](img122.gif) |
|||
![$\displaystyle \frac{1}{2}\Omega_0^2\left[1-\frac{1}{2}\left(e^{ika}+e^{-ika}\right)\right]$](img124.gif) |
|||
![$\displaystyle \frac{1}{2}\Omega_0^2\left[1-\cos(ka)\right]$](img125.gif) |
|||
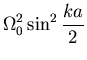 |
(3.16) |
![\framebox[0.9\textwidth]{\begin{minipage}{0.9\textwidth}\large\textcolor{red}{ D...
...n{equation}
\omega(k) = \Omega_0\sin\frac{ka}{2}
\end{equation}}\end{minipage}}](img127.gif)
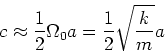
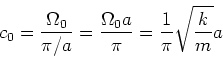
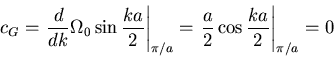
|
![\includegraphics[width=0.8\textwidth]{dispersion-federmodell-diatomic.eps}](img140.gif)
![\includegraphics[width=0.4\textwidth]{dispersion-diatomic.eps}](img141.gif)
Dispersionsrelation für Federketten mit zwei unterschiedlichen Atomen.
|
Wenn eine Federkette mit einer regelmässigen Anordnung zweier ungleicher Massen gebildet wird, tritt zum von
den vorherigen Ausführungen bekannten akustischen Zweig ein optischer Zweig. Zusätzlich gibt es
Frequenzen, für die es keinen reellen ![]() -Vektor gibt. Diese Frequenzen (oder über
-Vektor gibt. Diese Frequenzen (oder über ![]() auch
diese Energien) sind keine propagierenden Wellen möglich. Gibt es neben longitudinalen auch transversale
Wellen, zeigt die Dispersionsrelation nicht einen sondern drei Zweige akustischer Phononen.
auch
diese Energien) sind keine propagierenden Wellen möglich. Gibt es neben longitudinalen auch transversale
Wellen, zeigt die Dispersionsrelation nicht einen sondern drei Zweige akustischer Phononen.
Schwerewellen im tiefen Wasser haben die Dispersionsbeziehung
| (3.17) |
Eine Konsequenz ist, dass sehr lange Wellen sehr schnell sind (Bsp. Tsunamis)
Ein Puls oder eine Wellengruppe besteht aus Wellen benachbarter Frequenz. Analog zur
Modulation3.2 besteht ein Puls aus einer
Einhüllenden sowie einer Phase, die für sich aber keine Information trägt. Eine längere
Rechnung[Kän78] ergibt, dass die resultierende Wellenfunktion aus harmonischen Welle
![]() sowie der Modulation
sowie der Modulation
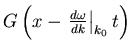 . Die resultierende
Welle ist
. Die resultierende
Welle ist
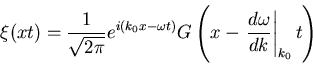 |
(3.18) |
![\framebox[0.9\textwidth]{\begin{minipage}{0.9\textwidth}\large\textcolor{red}{Di...
... v_G = \left.\frac{d\omega}{dk}\right\vert _{k_0}
\end{equation}}\end{minipage}}](img151.gif)
Bei unserem Feder-Masse-System ist ![]() wenn
wenn ![]() ist. Das heisst, der Puls, der die Information
trägt, ist ortsfest. Wenn
ist. Das heisst, der Puls, der die Information
trägt, ist ortsfest. Wenn ![]() nicht konstant ist, bewegen verändert sich die Form des Pulses, da
die verschiedenen Frequenzanteile sich unterschiedlich schnell ausbreiten.
nicht konstant ist, bewegen verändert sich die Form des Pulses, da
die verschiedenen Frequenzanteile sich unterschiedlich schnell ausbreiten.
Lösungsmöglichkeiten