
Weiter: Das Fermatsche Prinzip Oben: Physikalische Begründung der geometrischen Zurück: Reflexion Skript: PDF-Datei Übungen: Blätter
(Siehe Hecht, Optik [Hec, pp. 166]) (Siehe Pérez, Optik [Pér96, pp. 20]) (Siehe Tipler, Physik [TM04, pp. 1032])
|
|
Da jede Huygenssche Elementarwelle eine periodische Schwingung mit
einer gegebenen Frequenz ![]() darstellt, ändert sich die Frequenz beim
Übergang von einem Medium in das zweite nicht. Da die
Ausbreitungsgeschwindigkeit
darstellt, ändert sich die Frequenz beim
Übergang von einem Medium in das zweite nicht. Da die
Ausbreitungsgeschwindigkeit ![]() kleiner ist, gilt für die
Wellenlänge
kleiner ist, gilt für die
Wellenlänge
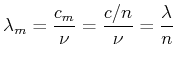 |
(4..5) |
In einem Medium mit einer Brechzahl ![]() ist die Wellenlänge kleiner.
So hat rotes Licht
ist die Wellenlänge kleiner.
So hat rotes Licht
![]() in Glas die Wellenlänge
in Glas die Wellenlänge
![]() .
.
![\includegraphics[width=0.6\textwidth]{brechung-geometrie}](img375.gif)
Geometrie der Brechung
|
Wir betrachten nun den Weg, den das Licht im Inneren eines Mediums zurücklegt.
Wir berücksichtigen, dass die Geschwindigkeit im Medium um den
Brechungsindex ![]() kleiner ist. Aus dem rechtwinkligen Dreieck wissen
wir, dass
kleiner ist. Aus dem rechtwinkligen Dreieck wissen
wir, dass
| (4..6) |
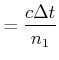 |
||
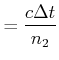 |
(4..7) |
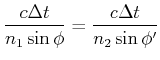 |
(4..8) |
Brechungsgesetz
|
Bei diesem Gesetz gibt es nur dann immer eine Lösung, wenn
![]() ist.
Sonst gibt es den Winkel der Totalreflexion. Wenn der vom optisch
dichteren Medium einfallende Lichtstrahl gegen die Grenzflächennormale den
Winkel
ist.
Sonst gibt es den Winkel der Totalreflexion. Wenn der vom optisch
dichteren Medium einfallende Lichtstrahl gegen die Grenzflächennormale den
Winkel
![]() hat und der Winkel des resultierenden Lichtstrahls gegen
die Grenzflächennormale im optisch dünneren Medium
hat und der Winkel des resultierenden Lichtstrahls gegen
die Grenzflächennormale im optisch dünneren Medium ![]() ist, hat das
Brechungsgesetz gerade noch eine reelle Lösung.
ist, hat das
Brechungsgesetz gerade noch eine reelle Lösung.
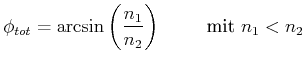 |
(4..10) |
Für Winkel, die grösser als
![]() sind, wird Licht aus dem optisch
dünneren Medium total reflektiert. Die Reflexion geschieht in einer
Tiefe von etwa
sind, wird Licht aus dem optisch
dünneren Medium total reflektiert. Die Reflexion geschieht in einer
Tiefe von etwa ![]() innerhalb des optisch dünneren Mediums.
innerhalb des optisch dünneren Mediums.
(Siehe Hecht, Optik [Hec, pp. 191]) (Siehe Pérez, Optik [Pér96, pp. 21]) (Siehe Tipler, Physik [TM04, pp. 1035]) (Siehe Gerthsen, Physik [Mes06, pp. 485])
|
|
|
|
![\includegraphics[width=0.6\textwidth]{reflexion-glasfaser}](img394.gif)
Transport von Licht in einer Stufenindexfaser
|
Wenn Licht mit einem Winkel nahe der Achse der optischen Faser in diese eingekoppelt wird, dann wird das Licht mit Totalreflexion transportiert. Nur Licht, das innerhalb des Akzeptanzwinkels den Faserkern trifft, wird weiter transportiert. Wenn die Faser gekrümmt wird, dann verlässt ein Teil des Lichtes die Faser: Krümmungen in der Faser erhöhen die Verluste.
Wenn der Faserkern den Durchmesser ![]() hat, ist der effektive Weg vom Winkel
hat, ist der effektive Weg vom Winkel
![]() gegen die Achse abhängig. Die Hypothenuse ist
gegen die Achse abhängig. Die Hypothenuse ist
![]() lang, der direkte Weg wäre
lang, der direkte Weg wäre
![]() . Die relative Längenänderung
ist
. Die relative Längenänderung
ist
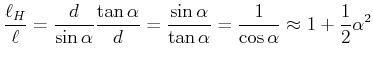 |
(4..11) |
| (4..12) |
| (4..13) |
Othmar Marti