
Weiter: Polarisation Oben: Physikalische Begründung der geometrischen Zurück: Brechung Skript: PDF-Datei Übungen: Blätter
(Siehe Hecht, Optik [Hec, pp. 166]) (Siehe Pérez, Optik [Pér96, pp. 13]) (Siehe Tipler, Physik [TM04, pp. 1042])
Eine alternative Art, die Ausbreitung von Licht zu beschreiben, ist das Fermatsche Prinzip.
| Der Weg, den das Licht nimmt, um von einem Punkt zu einem anderen zu gelangen, ist stets so, dass die benötigte Zeit minimal ist. |
Die genauere Formulierung lautet:
| Der Weg, den das Licht nimmt, um von einem Punkt zu einem anderen zu gelangen, ist stets so, dass die Zeit, die das Licht benötigt, invariant gegen kleine Änderungen des Weges ist. |
Mathematisch lautet das Fermatsche Prinzip: Die Zeit
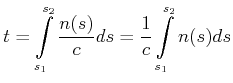 |
(4..14) |
Wenn man den Weg nicht kennt, kann man Testfunktionen
![]() verwenden.
Diejenige, die die kürzeste Zeit ergibt, ist die wahrscheinlichste.
verwenden.
Diejenige, die die kürzeste Zeit ergibt, ist die wahrscheinlichste.
![\includegraphics[width=0.3\textwidth]{fermat-reflexion}](img404.gif)
|
Ein Beispiel für das Fermatsche Prinzip ist die Reflexion. In der
obigen Zeichnung ist ![]() das an der Grenzfläche gespiegelte Bild von
das an der Grenzfläche gespiegelte Bild von ![]() . In
dem Dreieck
. In
dem Dreieck ![]() ist die Summe der Seitenlängen
ist die Summe der Seitenlängen ![]() und
und ![]() grösser als
die Seitenlänge
grösser als
die Seitenlänge ![]() . Da die Konstruktion mit
. Da die Konstruktion mit ![]() eine Hilfskonstruktion ist
und wir überall die gleiche Ausbreitungsgeschwindigkeit
eine Hilfskonstruktion ist
und wir überall die gleiche Ausbreitungsgeschwindigkeit ![]() haben, ist die
direkte Verbindung
haben, ist die
direkte Verbindung ![]() die kürzeste Strecke zwischen den beiden Punkten.
Damit ist aber das Gesetz Einfallswinkel = Ausfallswinkel gezeigt.
die kürzeste Strecke zwischen den beiden Punkten.
Damit ist aber das Gesetz Einfallswinkel = Ausfallswinkel gezeigt.
![\includegraphics[width=0.4\textwidth]{fermat-brechung}](img409.gif)
|
Zur Berechnung des Brechungsgesetzes nehmen wir an, dass das Licht von ![]() (gegeben) über 0 (verschiebbar, Koordinate
(gegeben) über 0 (verschiebbar, Koordinate ![]() ) nach
) nach ![]() (gegeben) sich
ausbreitet. Die Zeit, um von
(gegeben) sich
ausbreitet. Die Zeit, um von ![]() nach
nach ![]() ist
ist
| (4..15) |
 |
(4..16) |
 |
(4..17) |
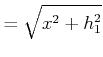 |
(4..18) | |
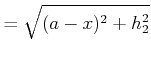 |
| 0 | 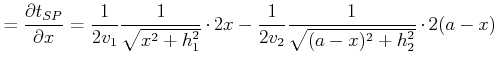 |
(4..19) |
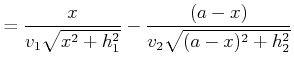 |
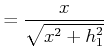 |
(4..20) | |
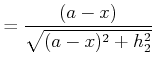 |
| (4..21) |
![\includegraphics[width=0.6\textwidth]{fermat-wege}](img427.gif)
Der kürzeste Weg
|
Vom Punkte ![]() soll Licht zum Punkte
soll Licht zum Punkte ![]() gelangen. Es gibt viele mögliche Wege.
nach dem Fermatschen Prinzip folgt Licht dem Weg, der sich am wenigsten in der
optischen Länge4.2 von seinen benachbarten Wegen unterscheidet. Wenn die
Weglängenfunktion stetig differenzierbar ist, ist dies auch der kürzeste Weg.
Wir berechnen nun die Phase einer Welle, die entlang eines beliebigen Weges
sich ausbreitet, wobei
gelangen. Es gibt viele mögliche Wege.
nach dem Fermatschen Prinzip folgt Licht dem Weg, der sich am wenigsten in der
optischen Länge4.2 von seinen benachbarten Wegen unterscheidet. Wenn die
Weglängenfunktion stetig differenzierbar ist, ist dies auch der kürzeste Weg.
Wir berechnen nun die Phase einer Welle, die entlang eines beliebigen Weges
sich ausbreitet, wobei ![]() ein Parameter ist, der die möglichen Wege
beschreibt.
ein Parameter ist, der die möglichen Wege
beschreibt.
Man nimmt an, dass alle Amplituden gleich sind und erhält
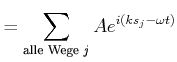 |
(4..22) | |
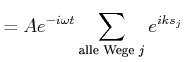 |
Die verbleibende Summation wird auf graphischem Wege in der komplexen Ebene durchgeführt. Die im Punkte B beobachtete Intensität ist das Resultat der Interferenz aller möglichen Wege.
![\includegraphics[width=0.6\textwidth]{kaenzig}](img435.gif)
Diese Darstellung zeigt grafisch die Summenbildung zur Berechnung der
Interferenz für alle möglichen Wege. Die einzelnen Amplituden werden
aufsummiert. Rot ist das Resultat dargestellt.
|
In dieser Abbildung tragen nur die Wege in der Nähe des kürzesten Weges zur
konstruktiven Interferenz bei. Nur dort ist die Ableitung der Weglänge gegen
den Parameter ![]() null: Alle Summanden interferieren konstruktiv. Die Wege über
null: Alle Summanden interferieren konstruktiv. Die Wege über
![]() und
und ![]() ändern die Länge schnell mit
ändern die Länge schnell mit ![]() . Sie bilden die beiden Spiralen
auf der linken und auf der rechten Seite und tragen nichts zur Summe bei. Wir
können das Fermatsche Prinzip auch so formulieren:
. Sie bilden die beiden Spiralen
auf der linken und auf der rechten Seite und tragen nichts zur Summe bei. Wir
können das Fermatsche Prinzip auch so formulieren:
| In der Quantenelektrodynamik werden Prozesse durch das Aufsummieren aller möglichen Feynmanschen Diagramme berechnet. Nur wenige Diagramme tragen zum Resultat wesentliches bei, die anderen sind Korrekturen höherer Ordnung. Die Summe Feynmanschen Diagramme ist nichts anderes als das Fermatsche Prinzip angewandt auf die Quantenelektrodynamik. |
Othmar Marti