
Weiter: Brechung Oben: Physikalische Begründung der geometrischen Zurück: Das Fresnel-Huygenssche Prinzip Skript: PDF-Datei Übungen: Blätter
|
|
![\includegraphics[width=0.6\textwidth]{reflexion-geometrie}](img339.gif)
|
Wir betrachten eine Welle, die sich mit dem Wellenvektor ![]() sich auf die Grenzfläche Luft-Glas hin bewegt. Eingezeichnet ist rot der
Wellenberg, der durch
sich auf die Grenzfläche Luft-Glas hin bewegt. Eingezeichnet ist rot der
Wellenberg, der durch ![]() zur Zeit
zur Zeit ![]() geht. Dieser Wellenberg berührt die
Grenzfläche in
geht. Dieser Wellenberg berührt die
Grenzfläche in ![]() . An beiden orten wird eine Huygenssche
Elementarwelle ausgelöst. nach der Zeit
. An beiden orten wird eine Huygenssche
Elementarwelle ausgelöst. nach der Zeit ![]() hat
der Wellenberg, der zur Zeit
hat
der Wellenberg, der zur Zeit ![]() durch
durch ![]() ging,
ging, ![]() erreicht. Nach dem
Huygensschen Prinzip hat auch die in
erreicht. Nach dem
Huygensschen Prinzip hat auch die in ![]() startende
Elementarwelle
startende
Elementarwelle ![]() erreicht. Die Elementarwelle aus
erreicht. Die Elementarwelle aus ![]() ist
nun bei
ist
nun bei ![]() . Da wir keine Annahme über Zeiten und Abstände gemacht haben, muss
diese Elementarwelle Teil eines konstruktiv überlagernden Systems von
Elementarwellen sein, die eine zweite ebene Welle mit dem Wellenvektor
. Da wir keine Annahme über Zeiten und Abstände gemacht haben, muss
diese Elementarwelle Teil eines konstruktiv überlagernden Systems von
Elementarwellen sein, die eine zweite ebene Welle mit dem Wellenvektor
![]() erzeugen. Da die Ausbreitungsgeschwindigkeit für die beiden
Elementarwellen gleich ist, da die Verbindungsstrecken
erzeugen. Da die Ausbreitungsgeschwindigkeit für die beiden
Elementarwellen gleich ist, da die Verbindungsstrecken
![]() und
und
![]() gleich lang sind und beide Teile eines rechtwinkligen Dreiecks
sind, müssen alle Winkel gleich sein. Deshalb ist der Neigungswinkel von
gleich lang sind und beide Teile eines rechtwinkligen Dreiecks
sind, müssen alle Winkel gleich sein. Deshalb ist der Neigungswinkel von ![]() zur Senkrechten gleich dem Neigungswinkel von
zur Senkrechten gleich dem Neigungswinkel von ![]() zur Senkrechten. Es
folgt das Reflexionsgesetz
zur Senkrechten. Es
folgt das Reflexionsgesetz
In einem Medium bewegt sich Licht langsamer: die Lichtwelle regt die gebundenen Elektronen zum Schwingen an. Diese erzeugen Huygenssche Elementarwellen, aber mit einer Phasenverschiebung oder, in anderen Worten, einer Zeitverzögerung. Dies bedeutet, dass Licht sich langsamer ausbreitet. Die Ausbreitungsgeschwindigkeit von Licht im Medium ist
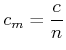 |
(4..1) |
wenn ![]() das elektrische Feld, d.h. die Amplitude der Lichtwelle ist.
das elektrische Feld, d.h. die Amplitude der Lichtwelle ist.
![]() ist die Dielektrische
Feldkonstante und
ist die Dielektrische
Feldkonstante und
![]() die Lichtgeschwindigkeit im Vakuum. Der Vorfaktor
die Lichtgeschwindigkeit im Vakuum. Der Vorfaktor
![]() kommt von der
Mittelung über viele Wellen her. Gleichung (4.2) kann auch so geschrieben
werden:
kommt von der
Mittelung über viele Wellen her. Gleichung (4.2) kann auch so geschrieben
werden:
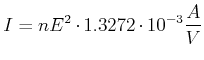 |
(4..3) |
Bei senkrechtem Einfall ist die Intensität des reflektierten Lichtes (ohne Beweis)
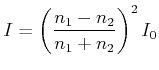 |
(4..4) |
Dabei sind ![]() und
und ![]() die Brechzahlen der beiden Medien und
die Brechzahlen der beiden Medien und ![]() die
einfallende Intensität. Bei
die
einfallende Intensität. Bei ![]() (Luft) und
(Luft) und ![]() (Wasser) ist
(Wasser) ist
![]() . Für
. Für ![]() (Glas) ist
(Glas) ist
![]() und für
und für ![]() (etwa Diamant) ist
(etwa Diamant) ist
![]() . Bei
. Bei ![]() ist
ist
![]() !
!
| Bei zwei Medien mit unterschiedlichen Brechzahlen heisst dasjenige das optisch dichtere Medium, dessen Brechzahl grösser ist. |
Othmar Marti