
Weiter: Die Fresnelschen Formeln Oben: Physikalische Begründung der geometrischen Zurück: Das Fermatsche Prinzip Skript: PDF-Datei Übungen: Blätter
(Siehe Hecht, Optik [Hec, pp. 475]) (Siehe Tipler, Physik [TM04, pp. 1044])
|
|
Licht ist eine transversale elektromagnetische Welle. Das heisst, dass das
elektrische und das magnetische Feld senkrecht zur Ausbreitungsrichtung
schwingen. Die Wellengleichung für das elektrische Feld und damit auch für
Licht ist durch
![]() ,
,![]() gegeben. Die Tatsache, dass wir
eine Transversalwelle haben erfordert, dass
gegeben. Die Tatsache, dass wir
eine Transversalwelle haben erfordert, dass ![]() der Bedingung
der Bedingung
| (4..23) |
Wenn wir nun, ohne Einschränkung der Allgemeinheit, die Ausbreitungsrichtung der Welle in die x-Richtung legen, dann sind
Diese Wahl erfüllt die Bedingung der Transversalität.
|
Es gibt zwei mögliche orthogonale Orientierungen von |
(Siehe Pérez, Optik [Pér96, pp. 323]) (Siehe Hecht, Optik [Hec, pp. 487]) (Siehe Tipler, Physik [TM04, pp. 1044])
|
|
![\includegraphics[width=0.6\textwidth]{Polarisation-Absorption}](img443.gif)
Polarisation durch Absorption in einem Drahtpolarisator
|
Wenn das elektrische Feld einer Mikrowellen entlang eines Drahtes zeigt, kann dieses Feld im Draht Ladungen bewegen und so Energie abgeben. Die Intensität der Welle und damit die die Absorption hängen von der Polarisation ab.
Ebenso gibt es Moleküle mit Doppelbindungen zwischen den Kohlenstoffatomen, bei
denen ![]() -Elektronen beweglich sind, die wie Drähte wirken. Werden diese
Moleküle orientiert zu einer Folie gemacht, so erhält man eine polarisierende
Folie.
-Elektronen beweglich sind, die wie Drähte wirken. Werden diese
Moleküle orientiert zu einer Folie gemacht, so erhält man eine polarisierende
Folie.
![\includegraphics[width=0.6\textwidth]{polarisator-analysator}](img445.gif)
![\includegraphics[width=0.6\textwidth]{polarisator-analysator-schraeg}](img446.gif)
Licht durch einen Polarisator und einen Analysator mit
gekreuzten Polarisationsrichtungen. Darunter die gleiche Anordnung, aber der
Analysator ist nun um
|
Bei einer Anordnung von Analysator und Polarisator
polarisiert der Polarisator das Licht. Der Analysator lässt
nur die Projektion des ![]() -Feldes auf seine Durchlassachse durch. Für die
Amplitude gilt
-Feldes auf seine Durchlassachse durch. Für die
Amplitude gilt
| (4..24) |
| (4..25) |
![\includegraphics[width=0.8\textwidth]{Dichroismus-NaVO4Mn}](img452.gif)
Dichroismus in einem
|
|
|
![\includegraphics[width=0.8\textwidth]{polarisation-streuung}](img453.gif)
Polarisation durch Streuung an einem Teilchen
|
Wenn Licht von links auf ein streuendes Teilchen (z.B. ein Wassertröpfchen)
fällt, dann kann nur die Komponente des ![]() -Feldes, die auch senkrecht
zur Streurichtung steht, eine Lichtwelle anregen. Die dazu senkrechte
Komponente würde eine propagierende, longitudinal polarisierte Welle erzeugen.
Propagierende, longitudinale Lichtwellen stehen aber im Widerspruch zu den
Maxwellschen Gleichungen und treten deshalb nicht auf.
-Feldes, die auch senkrecht
zur Streurichtung steht, eine Lichtwelle anregen. Die dazu senkrechte
Komponente würde eine propagierende, longitudinal polarisierte Welle erzeugen.
Propagierende, longitudinale Lichtwellen stehen aber im Widerspruch zu den
Maxwellschen Gleichungen und treten deshalb nicht auf.
(Siehe Hecht, Optik [Hec, pp. 509]) (Siehe Pérez, Optik [Pér96, pp. 320]) (Siehe Tipler, Physik [TM04, pp. 1047])
|
|
![\includegraphics[width=0.6\textwidth]{Polarisation-Brewster-Winkel}](img454.gif)
|
Wenn Licht in ein dichteres Medium eindringt und es zur Reflexion und zur Brechung kommt gelten zwei Gesetze
| (4..26) |
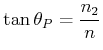 |
(4..27) |
(Siehe Hecht, Optik [Hec, pp. 492]) (Siehe Pérez, Optik [Pér96, pp. 322]) (Siehe Tipler, Physik [TM04, pp. 1048])
|
|
Viele Materialien haben isotrope optische Eigenschaften. Analog zu den
elastomechanischen Eigenschaften von isotropen Materialien, die durch den
Elastizitätsmodul ![]() beschrieben werden, werden isotrope optische Materialien
durch eine Brechzahl
beschrieben werden, werden isotrope optische Materialien
durch eine Brechzahl
![]() beschrieben. Die mechanischen
Eigenschaften anisotroper Materialien werden durch Tensoren beschrieben. Analog
werden optische Eigenschaften anisotroper Medien durch Tensoren
beschrieben. Die mechanischen
Eigenschaften anisotroper Materialien werden durch Tensoren beschrieben. Analog
werden optische Eigenschaften anisotroper Medien durch Tensoren
![]() oder
oder ![]() beschrieben. Die Mathematik sagt, dass solche Tensoren in einem
Hauptachsensystem Nur Komponenten auf ihrer Hauptdiagonalen haben. Für den
Brechungsindex heisst dies, dass nicht einer,
beschrieben. Die Mathematik sagt, dass solche Tensoren in einem
Hauptachsensystem Nur Komponenten auf ihrer Hauptdiagonalen haben. Für den
Brechungsindex heisst dies, dass nicht einer, ![]() sondern drei Indizes
sondern drei Indizes
![]() ,
, ![]() und
und ![]() angegeben werden müssen.
angegeben werden müssen.
|
![\includegraphics[width=0.6\textwidth]{lambda-viertel}](img465.gif)
Wirkungsweise eines
|
Bei einem ![]() - oder einem
- oder einem ![]() -Plättchen wird die
Polarisationsrichtung des einfallenden Lichtes so gewählt, dass sie
-Plättchen wird die
Polarisationsrichtung des einfallenden Lichtes so gewählt, dass sie ![]() zu
den beiden Hauptachsen mit
zu
den beiden Hauptachsen mit
![]() ist. Dann wird
die eine Welle wie in der unten stehenden
Zeichnung gezeigt, langsamer propagiert als die
andere (die rote). Es entsteht eine Phasenverschiebeung, die bei
ist. Dann wird
die eine Welle wie in der unten stehenden
Zeichnung gezeigt, langsamer propagiert als die
andere (die rote). Es entsteht eine Phasenverschiebeung, die bei
![]() -Plättchen gerade eine viertel Wellenlänge ausmacht. Das Licht ist
dann zirkular polarisiert.
-Plättchen gerade eine viertel Wellenlänge ausmacht. Das Licht ist
dann zirkular polarisiert.
![\includegraphics[width=0.9\textwidth]{lambda-viertel-welle}](img467.gif)
Wellen in einem
|
Ist der Gangunterschied ![]() , wie in der oben stehenden Zeichnung, dann
wird die Polarisationsrichtung um
, wie in der oben stehenden Zeichnung, dann
wird die Polarisationsrichtung um ![]() gedreht.
gedreht.
Wir beschreiben kohärentes Licht durch die Gleichung
| (4..28) |
wobei
![]() ist (Transversalität) und
ist (Transversalität) und ![]() die
Polarisationsrichtung angibt.
die
Polarisationsrichtung angibt. ![]() ist die Phase, die die Anfangsbedungung am
Ort 0 und zur Zeit 0 angibt.
ist die Phase, die die Anfangsbedungung am
Ort 0 und zur Zeit 0 angibt.
Ohne Einschränkung der Allgemeinheit können wir
![]() setzen.
Dann ist
setzen.
Dann ist
![]() die möglichen Polarisationsrichtungen. Der
Vektor des elektrischen Feldes hat also nur Komponenten in die
die möglichen Polarisationsrichtungen. Der
Vektor des elektrischen Feldes hat also nur Komponenten in die ![]() - und die
- und die
![]() -Richtung.
-Richtung.
Unser dichroitisches Plättchen habe die schnelle Achse (Brechungsindex
![]() ) entlang
) entlang ![]() und die langsame Achse (Brechungsindex
und die langsame Achse (Brechungsindex ![]() )
entlang
)
entlang ![]() und die Dicke
und die Dicke ![]() . Die
. Die ![]() -Achse sollen übereinstimmen. Das
gestrichene Koordinatensystem sei um den Winkel
-Achse sollen übereinstimmen. Das
gestrichene Koordinatensystem sei um den Winkel ![]() gegen das
ungestrichene verdreht. Dann ist
gegen das
ungestrichene verdreht. Dann ist
| (4..29) |
Für Licht mit einer beliebigen Polarisation und einer Ausbreitung entlang der
![]() -Achse muss das elektrische Feld auf das gestrichene Koordinatensystem
projiziert werden. Am Anfang des Plättchens sei zudem die Phase
-Achse muss das elektrische Feld auf das gestrichene Koordinatensystem
projiziert werden. Am Anfang des Plättchens sei zudem die Phase ![]() . Wir
bekommen dann
. Wir
bekommen dann
| (4..30) |
Die Feldkomponente mit der Polarisation ![]() breitet sich mit der
Geschwindigkeit
breitet sich mit der
Geschwindigkeit
![]() aus, die Polarisation
aus, die Polarisation ![]() mit der
Geschwindigkeit
mit der
Geschwindigkeit
![]() . Damit sind die Wellenlängen der Polarisation
entlang
. Damit sind die Wellenlängen der Polarisation
entlang ![]()
![]() und entlang
und entlang ![]()
![]() . Für die
. Für die ![]() gilt dann
gilt dann
| (4..31) |
Die Laufzeit durch ein Plättchen der Dicke ![]() ist dann
ist dann
![]() und
und
![]() . Wir betrachten zu einer
feststehenden Zeit (praktischerweise
. Wir betrachten zu einer
feststehenden Zeit (praktischerweise ![]() das Wellenmuster. Am Ausgang des
Plättchens haben wir
das Wellenmuster. Am Ausgang des
Plättchens haben wir
| (4..32) |
Der Phasenunterschied der beiden Wellen ist die Differenz der Argumente der
Exponentialfunktion, also
![]() Wir können also auch
schreiben
Wir können also auch
schreiben
| (4..33) |
Wenn wir den gemeinsamen Faktor abspalten, dann wird die ![]() -Komponente gegen
der
-Komponente gegen
der ![]() -Komponente um
-Komponente um
![]() phasenverschoben. Diese neuen
Polarisationen müssen wir auf das
phasenverschoben. Diese neuen
Polarisationen müssen wir auf das
![]() ,
,![]() ,
,![]() -Koordinatensystem mit
-Koordinatensystem mit
| (4..34) |
projizieren. Damit ist
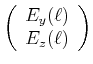 |
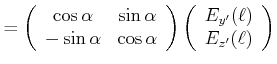 |
|
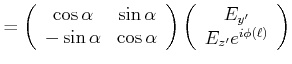 |
||
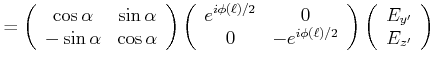 |
(4..35) | |
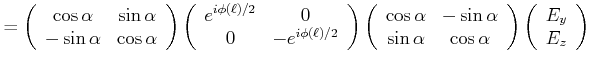 |
Ausmultipliziert erhält man für die Matrix
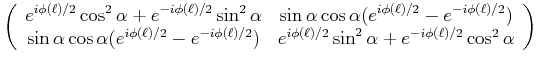 |
(4..36) |
oder (nur für die Matrix)
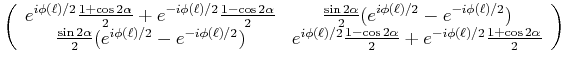 |
(4..37) |
Wir vereinfachen und erhalten die Matrix
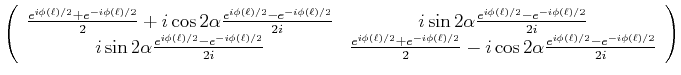 |
(4..38) |
und erhalten
Wir betrachten nun den Spezialfall, dass
![]() und
und
![]() ist. Die obige Matrix wird dann
ist. Die obige Matrix wird dann
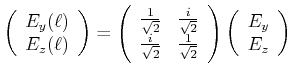 |
(4..40) |
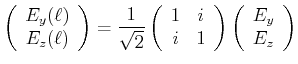 |
(4..41) |
Eine Lichtwelle, die nur in ![]() -Richtung polarisiert ist, wird zu einer Welle, die sowohl in die
-Richtung polarisiert ist, wird zu einer Welle, die sowohl in die ![]() wie
auch in die
wie
auch in die ![]() -Richtung polarisiert ist, aber mit einem Phasenfaktor von
-Richtung polarisiert ist, aber mit einem Phasenfaktor von
![]() . Die Wellengleichung ist dann
. Die Wellengleichung ist dann
| (4..42) |
Diese Art Wellen heisst zirkular polarisierte
Welle. Es gibt zwei Arten, mit rechtsläufigem und
linksläufigem Drehsinn. Ein dichroitisches Objekt, dass die obigen
Eigenschaften hat, heisst ![]() -Plättchen.
-Plättchen.
![\includegraphics[width=0.9\textwidth]{lambda-halbe-welle}](img535.gif)
Wellen in einem
|
Der zweite wichtige Spezialfall ist
![]() und
und
![]() .
Die obige Matrix wird dann
.
Die obige Matrix wird dann
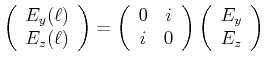 |
(4..43) |
Licht mit einer Polarisationsrichtung in ![]() -Richtung wird in Licht mit einer
Polarisationsrichtung
-Richtung wird in Licht mit einer
Polarisationsrichtung ![]() überführt. Eine solche Anordnung heisst
überführt. Eine solche Anordnung heisst
![]() -Plättchen. Zwei
-Plättchen. Zwei ![]() -Plättchen hintereinander geschaltet
haben die gleiche Wirkung. Anwendung: optisches Lesesystem in CDs.
-Plättchen hintereinander geschaltet
haben die gleiche Wirkung. Anwendung: optisches Lesesystem in CDs.
(Siehe Hecht, Optik [Hec, pp. 544])
Die Änderung der Polarisation von kohärentem Licht beim Durchgang durch Polarisatoren oder doppelbrechende Materialien kann mit Jones-Vektoren und Jones-Matrizen beschrieben werden. Jones-Vektoren und Jones-Matrizen sind eine Verallgemeinerung der obigen Rechnung. Formal läuft dies darauf hinaus, dass wir den Ausgangszustand al Vektor beschreiben und auf ihn die Operatoren der polarisationsändernden Objekte anwenden.
Aus der Darstellung im vorhergehenden Kapitel geht hervor, dass nur die ![]() -
und die
-
und die ![]() -Richtung die Polarisation beschreiben. Wir können also
Zweiervektoren verwenden. Weiter soll die Phase der Welle als komplexe Zahl
dargestellt werden. Schliesslich normieren wir die Länge des Vektors auf
-Richtung die Polarisation beschreiben. Wir können also
Zweiervektoren verwenden. Weiter soll die Phase der Welle als komplexe Zahl
dargestellt werden. Schliesslich normieren wir die Länge des Vektors auf ![]() .
Eine Welle polarisiert in die
.
Eine Welle polarisiert in die ![]() -Richtung wird also durch den Vektor
-Richtung wird also durch den Vektor
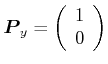 |
(4..44) |
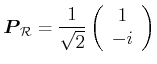 |
(4..45) |
| Jones-Vektoren | Beschreibung |
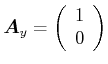 |
Linear polarisiert in |
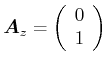 |
Linear polarisiert in |
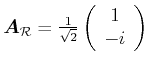 |
Rechtshändig zirkular polarisiert |
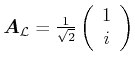 |
Linkshändig zirkular polarisiert |
Polarisationen in andere Richtungen können durch die Anwendung von Drehmatrizen
berechnet werden. Die Drehung aus dem Koordinatensystem
![]() ,
,![]() nach
nach
![]() ,
,![]() wird durch
wird durch
| (4..46) |
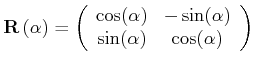 |
(4..47) |
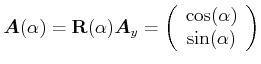 |
(4..48) |
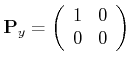 |
(4..49) |
| (4..50) | ||
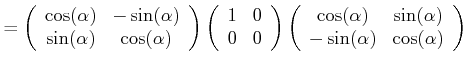 |
||
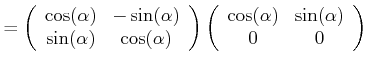 |
||
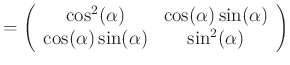 |
(4..51) |
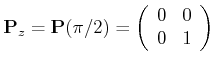 |
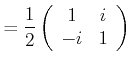 |
(4..52) | |
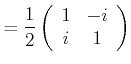 |
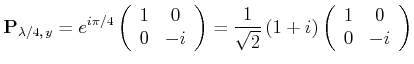 |
(4..53) |
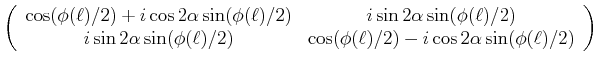 |
(4..54) |
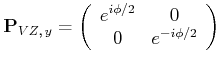 |
(4..55) |
| Jones-Matrix | Bedeutung |
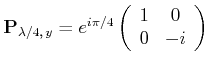 |
|
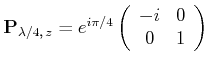 |
|
|
|
|
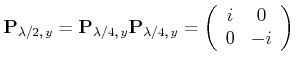 |
|
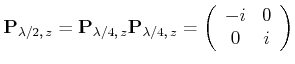 |
|
|
|
Wenn ein Lichtstrahl mit der Polarisation ![]() durch die Objekte
durch die Objekte
![]() ,
,![]() ,
,![]() ,
,![]() geht, ist die
resultierende Welle
geht, ist die
resultierende Welle
| (4..56) |
![\includegraphics[width=0.7\textwidth]{kalkspat}](img578.gif)
Aufspaltung eines Lichtstrahls in einem doppelbrechenden Material wie
Kalkspat
|
(Siehe Gerthsen, Physik [Mes06, pp. 535])
![\includegraphics[width=0.8\textwidth]{Doppelbrechung-NaVO4Mn}](img579.gif)
Doppelbrechung in einem
|
Viele Kristalle sind nicht isotrop. Es gib auch in diesen Kristallen Achsen,
die eine höhere Symmetrie aufweisen, als die anderen Achsen. Diese Achse wird
Hauptachse genannt. Alle physikalischen Eigenschaften eines Kristalls,
also auch die optischen Eigenschaften, müssen die Symmetrie des Kristalls
haben. Die physikalischen Eigenschaften und insbesondere die
Lichtgeschwindigkeit sind in allen Ebenen senkrecht zur Hauptachse
isotrop. Dabei ist die Lichtgeschwindigkeit aber von der Polarisationsrichtung
des Lichtes abhängig. In Richtung der Hauptachse ist die Lichtgeschwindigkeit
unabhängig von der Polarisationsrichtung ![]() . Licht, das sich senkrecht zur
Polarisationsrichtung ausbreitet, bewegt sich ebenfalls mit
. Licht, das sich senkrecht zur
Polarisationsrichtung ausbreitet, bewegt sich ebenfalls mit ![]() , wenn der
, wenn der
![]() -Vektor in Richtung der Hauptachse zeigt, die Polarisationsrichtung
also senkrecht zur Hauptachse liegt. Dieses licht heisst ordentliches
Licht. Licht mit der anderen Polarisationsrichtung läuft im Kalkspat
schneller, und zwar mit
-Vektor in Richtung der Hauptachse zeigt, die Polarisationsrichtung
also senkrecht zur Hauptachse liegt. Dieses licht heisst ordentliches
Licht. Licht mit der anderen Polarisationsrichtung läuft im Kalkspat
schneller, und zwar mit
![]() . Dieses Licht heisst
ausserordentliches Licht. Wenn die Einfallsrichtung dazwischen liegt,
ist die Geschwindigkeit des ordentlichen Lichts immer noch
. Dieses Licht heisst
ausserordentliches Licht. Wenn die Einfallsrichtung dazwischen liegt,
ist die Geschwindigkeit des ordentlichen Lichts immer noch ![]() , die des
ausserordentlichen Lichts liegt zwischen
, die des
ausserordentlichen Lichts liegt zwischen ![]() und
und ![]() .
.
Die Wellenflächen des ordentlichen Lichts stammend von einer punktförmigen Quelle sind also Kugelflächen, während die Wellenflächen des ausserordentlichen Lichts Rotationsellipsoide sind, deren Rotationsachse mit der Hauptachse parallel ist. Bei Kalkspat ist das Rotationsellipsoid abgeplattet, das Material heisst einachsig negativ. Bei Quarz ist das Rotationsellipsoid länglich (die ordentliche Lichtgeschwindigkeit ist grösser als die ausserordentliche.). Man nennt Quarz deshalb einachsig positiv.
Wenn Licht senkrecht auf eine Fläche fällt, die schräg zur Hauptachse liegt, müssen zwei verschiedene Konstruktionen verwendet werden:
Da die resultierenden Flächen Tangentenflächen sind, bleibt die Richtung des ordentlichen Lichtes senkrecht zur Oberfläche, während das ausserordentliche Licht sich schräg weiter ausbreitet. Zur Berechnung des Lichtweges müssen Tensoren verwendet werden.
In der Technik war die spannungsinduzierte Doppelbrechung lange das einzige Mittel, unzulässige Beanspruchungen in Bauteilen festzustellen.
|
|
Othmar Marti