
Weiter: Interferenz und Beugung Oben: Physikalische Begründung der geometrischen Zurück: Polarisation Skript: PDF-Datei Übungen: Blätter
(Siehe Hecht, Optik [Hec, pp. 175]) (Siehe Gerthsen, Physik [Mes06, pp. 539])
|
|
![\includegraphics[width=0.6\textwidth]{s-p-polarisation}](img585.gif)
|
Die Reflexion und die Brechung von Licht wird durch die Fresnelschen Formeln bestimmt. Wir verwenden die Definitionen
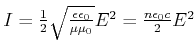 für sinusförmige Wellen
mit der Amplitude
für sinusförmige Wellen
mit der Amplitude Im folgenden betrachten wir nur nichtmagnetische Materialien.
Wir beginnen die Rechnungen für Licht mit einer Polarisation senkrecht zur Einfallsebene (s-Polarisation).
Wenn in den beiden angrenzenden Medien die Dielektrizitätskonstanten
![]() und
und
![]() sind, dann muss der Energiestrom an
der Grenzfläche kontinuierlich sein, also
sind, dann muss der Energiestrom an
der Grenzfläche kontinuierlich sein, also
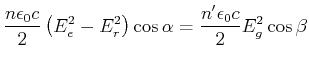 |
(4..57) |
wobei ![]() und
und ![]() die Winkel zur Oberflächennormalen sind,
die Winkel zur Oberflächennormalen sind,
![]() ist die
ist die ![]() -Feldkomponente des einfallenden Lichtes parallel zur
Oberfläche,
-Feldkomponente des einfallenden Lichtes parallel zur
Oberfläche, ![]() die des reflektierten (beachte das Vorzeichen) und
die des reflektierten (beachte das Vorzeichen) und
![]() die des gebrochenen.
die des gebrochenen.
Vereinfacht kann man die Energieerhaltung schreiben als
| (4..58) |
Die Komponente von ![]() parallel zur Oberfläche muss stetig sein,
also ist
parallel zur Oberfläche muss stetig sein,
also ist
![]() .
.
Wir beachten, dass
![]() ist und dividieren die beiden
Gleichungen durcheinander. Wir erhalten
ist und dividieren die beiden
Gleichungen durcheinander. Wir erhalten
| (4..59) |
Nach dem Brechungsgesetz ist
![]() . Wir setzen dies
ein und erhalten
. Wir setzen dies
ein und erhalten
| (4..60) |
Mit
![]() bekommen wir
bekommen wir
Fresnelsche Formeln für die Intensität bei der s-Polarisation für
nichtmagnetische Materialien
|
Wir haben die einfallende Intensität
![]() als
Referenz verwendet. Deshalb erscheint der Vorfaktor
als
Referenz verwendet. Deshalb erscheint der Vorfaktor
![]() für
für ![]() .
.
![\includegraphics[width=0.8\textwidth]{reflexion-parallel}](img619.gif)
Stetigkeitsbedingungen für Licht mit
p-Polarisation. Die dicken Vektoren stellen die
|
Bei ![]() -polarisiertem Licht ist die Bedingung für die Stetigkeit der
Parallelkomponente von
-polarisiertem Licht ist die Bedingung für die Stetigkeit der
Parallelkomponente von ![]() durch
durch
| (4..63) |
gegeben. Weiter gilt immer noch die Energieerhaltung
| (4..64) |
Teilen wir die beiden Gleichungen, erhalten wir
| (4..65) |
Wir wenden wieder das Snelliussche Gesetz an
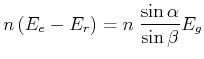 |
(4..66) |
Damit müssen wir das Gleichungssystem
lösen. Wir multiplizieren die erste Gleichung mit
![]() und die zweite
mit
und die zweite
mit ![]() und addieren
und addieren
| (4..68) |
Mit
![]() wird die obige Gleichung
wird die obige Gleichung
| (4..69) |
Um ![]() zu bekommen multiplizieren wir die obere Gleichung in
Gleichung (4.67) mit
zu bekommen multiplizieren wir die obere Gleichung in
Gleichung (4.67) mit ![]() und die untere mit
und die untere mit
![]() ,
subtrahieren und erhalten
,
subtrahieren und erhalten
| (4..70) |
Dies ist auch
| (4..71) |
Damit erhält man
Wenn in der Gleichung für ![]()
![]() ist, divergiert
der Nenner, wir erhalten also
ist, divergiert
der Nenner, wir erhalten also
![]() . Dies ist
der Brewster-Winkel.
. Dies ist
der Brewster-Winkel.
Die Fresnelschen Formeln für die Intensität lauten
![\includegraphics[width=0.8\textwidth]{fresnel-e}](img644.gif)
Verlauf der Amplitude des elektrischen Feldes für
p- und
s-Polarisation, wenn Licht aus dem dünneren
Medium (
|
![\includegraphics[width=0.8\textwidth]{fresnel-er}](img648.gif)
Verlauf der Amplitude des elektrischen Feldes für
p- und
s-Polarisation, wenn Licht aus dem dichteren
(
|
Wir können kontrollieren, ob im Energiefluss senkrecht zur Grenzfläche die Energie erhalten bleibt. Dazu müssen wir den Energiefluss durch eine Fläche parallel zur Oberfläche berechnen. Der einfallende Energiefluss ist
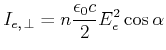 |
(4..74) |
Der Fluss der reflektierten Energie durch eine Fläche parallel zur Grenzfläche ist
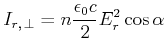 |
(4..75) |
Ebenso ist der Fluss der gebrochenen Energie durch eine Fläche parallel zur Grenzfläche
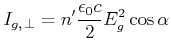 |
(4..76) |
Die Energieerhaltung sagt nun, dass für die ![]() -Polarisation
-Polarisation
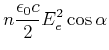 |
||
![$\displaystyle n \frac{\epsilon_0 c}{2}E_e^2\frac{\tan^2[\alpha-\beta(\alpha)]}{\tan^2[\alpha+\beta(\alpha)]}\cos{\alpha}$](img659.gif) |
||
![$\displaystyle + n' \frac{\epsilon_0 c}{2} E_e^2\frac{4\sin^2\beta(\alpha)\cos^2...
...a}{\sin^2[\alpha+\beta(\alpha)]\cos^2[\alpha-\beta(\alpha)]}\cos(\beta(\alpha))$](img660.gif) |
||
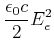 |
||
![$\displaystyle \left[n\frac{\sin^2[\alpha-\beta(\alpha)] \cos^2[\alpha-\beta(\alpha)]\cos\alpha}{\sin^2[\alpha+\beta(\alpha)]\cos^2[\alpha-\beta(\alpha)]}\right.$](img662.gif) |
||
![$\displaystyle +\left.n' \frac{4\sin^2\beta(\alpha)\cos^2\alpha\cos(\beta(\alpha))}{\sin^2[\alpha+\beta(\alpha)]\cos^2[\alpha-\beta(\alpha)]}\right]$](img663.gif) |
||
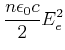 |
||
![$\displaystyle +\left. \frac{\sin\alpha}{\sin\beta\left(\alpha\right)}4\sin^2\beta\left(\alpha\right)\cos^2\alpha\cos\left(\beta\left(\alpha\right)\right)\right]$](img666.gif) |
||
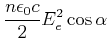 |
||
| (4..77) |
gilt.
Wir müssen also den Wert des Bruches
| (4..78) | ||
![$\displaystyle \left\{\frac{1}{2}\left(1-\cos[2\alpha-2\beta]\right)\frac{1}{2}\left(1+\cos[2\alpha+2\beta]\right)\right.$](img677.gif) |
||
![$\displaystyle \cdot\left\{\frac{1}{2}\left(1-\cos[2\alpha+2\beta]\right)\frac{1}{2}\left(1+\cos[2\alpha-2\beta]\right)\right\}^{-1}$](img679.gif) |
||
Wir setzen
![]() und
und
![]() und
schreiben die Gleichung um
und
schreiben die Gleichung um
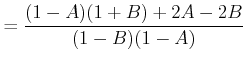 |
(4..79) | |
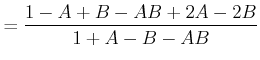 |
||
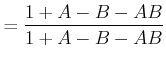 |
||
Da ![]() ist, ist gezeigt, dass für den Energiefluss durch die Grenzfläche für
ist, ist gezeigt, dass für den Energiefluss durch die Grenzfläche für
![]() -Polarisation Energieerhaltung gilt.
-Polarisation Energieerhaltung gilt.
Eine ähnliche Gleichung kann man für die ![]() -Polarisation berechnen. In der
Elektrizitätslehre würde man sagen, dass der Fluss des Pointing-Vektors
berechnet wurde.
-Polarisation berechnen. In der
Elektrizitätslehre würde man sagen, dass der Fluss des Pointing-Vektors
berechnet wurde.
Parallel zur Oberfläche ist es wegen der Translationssymmetrie schwieriger Energieerhaltungsgrössen zu definieren.
Die dritte Stetigkeitsbedingung an der Grenzfläche, die der Normalkomponente
von
![]() liefert das Snelliussche Gesetz.
liefert das Snelliussche Gesetz.
(Siehe Hecht, Optik [Hec, pp. 193,196])
|
|
Aus den letzten Abbildungen ist ersichtlich, dass wenn Licht aus dem dichteren
Medium in das dünnere eintritt, es Winkel gibt (
![]() , für die es
keine reelle Lösung der Fresnelschen Formeln gibt. Die Lösung ist rein
imaginär. Was bedeutet dies? Dies heisst, dass auch der
, für die es
keine reelle Lösung der Fresnelschen Formeln gibt. Die Lösung ist rein
imaginär. Was bedeutet dies? Dies heisst, dass auch der ![]() -Vektor des
Lichtes im dünneren Medium imaginär wird. Darum wird aus
-Vektor des
Lichtes im dünneren Medium imaginär wird. Darum wird aus ![]() mit
mit
![]() der exponentielle Dämpfungsfaktor
der exponentielle Dämpfungsfaktor
![]() , wobei
, wobei ![]() vom
Einfallswinkel abhängt. Licht im dünneren Medium kann also nicht propagieren:
Wegen der Energieerhaltung ist die Reflexion perfekt.
vom
Einfallswinkel abhängt. Licht im dünneren Medium kann also nicht propagieren:
Wegen der Energieerhaltung ist die Reflexion perfekt.
![\includegraphics[width=0.8\textwidth]{totalreflexion}](img703.gif)
Momentaufnahme der Interferenz einer
total reflektierten Welle mit sich selber sowie der evaneszenten Wellen.
|
Othmar Marti