
Weiter: Phasendifferenz und Kohärenz Oben: Vorlesungsskript PHYS2110 Grundlagen der Zurück: Die Fresnelschen Formeln Skript: PDF-Datei Übungen: Blätter
|
|
In diesem Abschnitt sollen die Eigenschaften von Licht, die auf der Wellennatur beruhen, diskutiert werden.
![\includegraphics[width=0.6\textwidth]{welle_interferenz}](img704.gif)
Interferenz zweier Wellen mit der gleichen Amplitude und der
gleichen Frequenz und einer Phase, die von
|
Mathematisch setzen wir zwei Wellen an
| (5..1) |
| (5..2) |
| (5..3) |
Wir wenden die Additionstheoreme für die Winkelfunktionen an. Wir verwenden
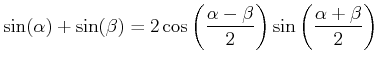 |
(5..4) |
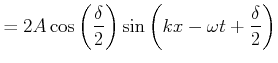 |
(5..5) |
|