Wellen in 2 und mehr Dimensionen

(Siehe Gerthsen, Physik [Mes06, pp. 160]) (Siehe Hecht, Optik [Hec, pp. 41])

Versuch zur Vorlesung: Wellenwanne (Versuchskarte O-021)

Die Wellenfunktion für eine zeitunabhängige Welle in zwei oder drei Dimensionen wird wie

$$\Psi(\vec{x},t) = \Psi_0(\vec{x}) \cos[\vec{k}(\vec{x}) \cdot \vec{x}-\omega t]$$ (5..43)

für eine longitudinale Welle und

$$\vec{A}(\vec{x},t) = \vec{A}_0(\vec{x}) \cos[\vec{k}(\vec{x}) \cdot \vec{x}-\omega t]$$ (5..44)

für transversale Wellen. $\vec{A}$ ist ein Vektor, der auch komplexe Komponenten haben kann (Die komplexen Komponenten geben die Phasen an.). Der Vektor, der aus dem Betrag der einzelnen Komponenten gebildet wird, gibt die Schwingungsrichtung der Welle an. Für eine transversale Welle gilt

$$\vec{A}(\vec{x}) \cdot \vec{k}(\vec{x}) = 0$$ (5..45)

Ebene Wellen

Bild einer ebenen Welle

Eine ebene Welle entsteht aus der allgemeinen Wellengleichung dadurch, dass die Amplitude und der Wellenvektor nicht vom Ort abhängen. Eine ebene Transversalwelle ist durch

$$\vec{A}(\vec{x}) = \vec{A}_0 \cos(\vec{k}\cdot \vec{x}- \omega t)$$ (5..46)

eine Longitudinalwelle durch

$$\Psi(\vec{x}) = \Psi_0 \cos(\vec{k}\cdot \vec{x}- \omega t)$$ (5..47)

gegeben. Ebene Wellen können durch einen Vektor, der die Ausbreitungsrichtung anzeigt, dargestellt werden. Bei ebenen Lichwellen spricht man dann von Lichtstrahlen.

Kugelwellen

(Siehe Hecht, Optik [Hec, pp. 48, 710]) (Siehe Pérez, Optik [Pér96, pp. 287])

Versuch zur Vorlesung: Wellenwanne (Versuchskarte O-021)

Eine weitere häufig vorkommende Form von Wellen sind die Kugelwellen. Wir können die Amplitudenabhängigkeit durch folgende Überlegung erhalten.

• Wir denken uns eine Kugeloberfläche um die Quelle, wobei die Quelle im Mittelpunkt der Kugel sein soll.
• Der Energiefluss pro Zeit, die Leistung, die durch die gesamte Kugeloberfläche fliesst ist konstant, unabhängig vom Radius der Kugel.
• Damit diese Gleichung für alle $r$ gilt muss $A(r) = A_0\frac{r_0}{r}$ sein.

Amplitude und Intensität einer Kugelwelle in Abhängigkeit der Distanz $r$ von der Quelle. Links eine lineare, rechts eine logarithmische Darstellung.

Bei einer Kugelwelle ist

• die Amplitude: $A(r) = A_0\frac{r_0}{r}$
• die Intensität $I(r) = I_0\frac{r_0^2}{r^2}$

Versuch zur Vorlesung: Moire-Modell der Interferenz von Kugelwellen (Versuchskarte O-019)

Interferenz bei Moire-Mustern

Der erste Summand beschreibt die Interferenz, während der zweite die nur vorhanden ist, wenn die beiden Amplituden $E_1$ und $E_2$ verschieden sind.

Interferenz zweier Wellen aus $A$ und $B$

Aus der Zeichnung ist ersichtlich, dass der Weglängenunterschied von $A$ nach $P$ und von $B$ nach $P$ $\Delta\ell = d\sin \varphi$ ist. Aus Gleichung (5.6) wissen wir, dass konstruktive Interferenz auftritt, wenn

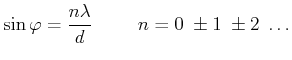$$\sin\varphi = \frac{n\lambda}{d}\hspace{1cm} n = 0,\;\pm 1,\;\pm 2,\;\ldots$$ (5..48)

ist. In der paraxialen Näherung (kleine $\varphi$) gilt auch

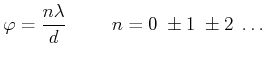$$\varphi = \frac{n\lambda}{d}\hspace{1cm} n = 0,\;\pm 1,\;\pm 2,\;\ldots$$ (5..49)

Interferenzminima treten bei

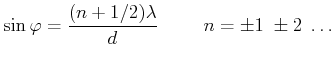$$\sin\varphi = \frac{(n+1/2)\lambda}{d}\hspace{1cm} n = \pm 1,\;\pm 2,\;\ldots$$ (5..50)

oder, in der paraxialen Näherung (kleine $\phi$), bei

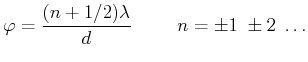$$\varphi = \frac{(n+1/2)\lambda}{d}\hspace{1cm} n = \pm 1,\;\pm 2,\;\ldots$$ (5..51)

Die Lage der Interferenzextrema hängen von der Wellenlänge ab.