
Weiter: Vektoraddition von harmonischen Wellen Oben: Interferenz und Beugung Zurück: Wellen in 2 und Skript: PDF-Datei Übungen: Blätter
(Siehe Hecht, Optik [Hec, pp. 572]) (Siehe Pérez, Optik [Pér96, pp. 358]) (Siehe Tipler, Physik [TM04, pp. 1116])
|
|
![\includegraphics[width=0.8\textwidth]{doppelspalt}](img874.gif)
Strahlengang bei einem Doppelspalt
|
Aus den Interferenzbedingungen wissen wir, dass wir
konstruktive Interferenz (helle Streifen) bei
destruktive Interferenz (dunkle Streifen) bei
|
haben. Wir berechnen nun den Verlauf der Intensität.
Am Punkt ![]() ist die Phasendifferenz
ist die Phasendifferenz
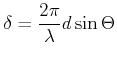 |
(5..54) |
Der ![]() -te helle Streifen hat von der Achse den Abstand
-te helle Streifen hat von der Achse den Abstand ![]() . Nach der Skizze
ist der Winkel dann durch
. Nach der Skizze
ist der Winkel dann durch
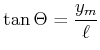 |
(5..55) |
gegeben. Wir verwenden, dass für kleine Winkel ![]() gilt:
gilt:
![]() . Damit folgt
. Damit folgt
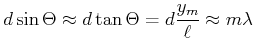 |
(5..56) |
Der ![]() -te helle Streifen liegt also bei
-te helle Streifen liegt also bei
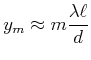 |
(5..57) |
Der Abstand zweier Streifen ist
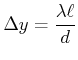 |
(5..58) |
Wenn wir die Amplituden der Felder verwenden (die elektrischen Felder ![]() ),
können wir sagen, dass die beiden Felder
),
können wir sagen, dass die beiden Felder
![]() und
und
![]() am Punkt
am Punkt ![]() interferieren.
interferieren.
| (5..59) |
Mit
![]()
bekommt man
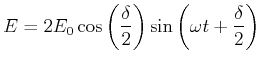 |
(5..60) |
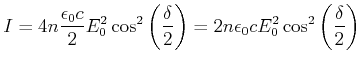 |
(5..61) |
wobei ![]() der Brechungsindex des Mediums ist. Mit
der Brechungsindex des Mediums ist. Mit
![]() wird die Phase
wird die Phase
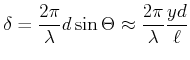 |
(5..62) |
und
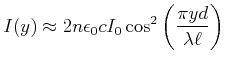 |
(5..63) |
![\includegraphics[width=0.25\textwidth]{doppelspalt-3}](img893.gif)
![\includegraphics[width=0.25\textwidth]{doppelspalt-10}](img894.gif)
![\includegraphics[width=0.25\textwidth]{doppelspalt-30}](img895.gif)
Beugung an einem Doppelspalt. Links ist
|
Die Interferenz an einem Doppelspalt hängt von der Polarisationsrichtung ab.
|
|
Othmar Marti