
Weiter: Wellen in 2 und Oben: Interferenz und Beugung Zurück: Interferenz und Beugung Skript: PDF-Datei Übungen: Blätter
(Siehe Hecht, Optik [Hec, pp. 570]) (Siehe Pérez, Optik [Pér96, pp. 367]) (Siehe Tipler, Physik [TM04, pp. 1109]) (Siehe Gerthsen, Physik [Mes06, pp. 514])
Wir betrachten Wellen, die sich auf verschiedenen Wegen ausbreiten.
| Zwei Wellen heissen kohärent, wenn sie, bis auf eine Phase die gleiche Zeitabhängigkeit haben. |
|
|
Die Kohärenz von Wellen ist nur im Idealfall überall und zu jeder Zeit gegeben.
Hat eine Quelle (ein gedämpfter harmonischer Oszillator) eine Bandbreite
![]() , dann ist die Kohärenzzeit
, dann ist die Kohärenzzeit
![]() und
und
![]() .
.
Ist die Lichtquelle ausgedehnt (Breite ![]() ), dann gibt es nur im Winkelbereich
), dann gibt es nur im Winkelbereich
![]() eine kohärente Überlagerung.
eine kohärente Überlagerung.
Die Intensität muss verschieden berechnet werden, je nachdem ob die
beiden Wellenzüge mit den Amplituden ![]() und
und ![]() kohärent oder nicht sind.
kohärent oder nicht sind.
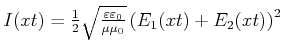
![$ I(x,t) =
\frac{1}{2}\sqrt{\frac{\varepsilon\varepsilon_0}{\mu\mu_0}}\left[E_1(x,t)^2+E_2(x,t)^2\right]$](img730.gif)
Bei kohärenten Wellen mit dem Phasenunterschied ![]() und den Amplituden
und den Amplituden ![]() und
und ![]() ist die resultierende Amplitude
ist die resultierende Amplitude
(Siehe Hecht, Optik [Hec, pp. 431]) (Siehe Pérez, Optik [Pér96, pp. 293]) (Siehe Tipler, Physik [TM04, pp. 435]) (Siehe Gerthsen, Physik [Mes06, pp. 513])
Wenn wir eine nach links laufende Welle
![]() und
eine nach rechts laufende Welle
und
eine nach rechts laufende Welle
![]() zur
Interferenz kommen lassen, erhalten wir
zur
Interferenz kommen lassen, erhalten wir
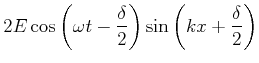 |
(5..7) |
| Stehende Wellen als Resultat zweier gegenläufiger Wellen gibt es in jedem Resonator, insbesondere in Laserresonatoren. |
(Siehe Hecht, Optik [Hec, pp. 596]) (Siehe Pérez, Optik [Pér96, pp. 360]) (Siehe Tipler, Physik [TM04, pp. 1114])
|
|
![\includegraphics[width=0.6\textwidth]{michelson}](img743.gif)
Aufbau des Michelson-Interferometers.
|
Beim Michelson-Interferometer wird Licht durch einen Strahlteiler in zwei
Lichtwege aufgespalten. Der Weg vom Strahlteiler zum festen Spiegel sei
![]() , der zum beweglichen
, der zum beweglichen ![]() . Deshalb ist der gesamte
Weglängenunterschied
. Deshalb ist der gesamte
Weglängenunterschied
![]() . Immer wenn
. Immer wenn
![]() ein ganzzahliges Vielfaches der Wellenlänge
ein ganzzahliges Vielfaches der Wellenlänge ![]() ist, tritt konstruktive
Interferenz auf. Wird der bewegliche Spiegel um
ist, tritt konstruktive
Interferenz auf. Wird der bewegliche Spiegel um ![]() verschoben, ändert
sich
verschoben, ändert
sich
![]() um
um ![]() , dann haben wir destruktive Interferenz.
, dann haben wir destruktive Interferenz.
Wenn wir das Interferometer mit einer Intensität von ![]() betreiben
und wenn wir eine Intensitätsänderung von
betreiben
und wenn wir eine Intensitätsänderung von ![]() noch messen können, dann
können wir die mögliche Distanzauflösung in nichtmagnetischen Medien wie folgt
berechnen:
noch messen können, dann
können wir die mögliche Distanzauflösung in nichtmagnetischen Medien wie folgt
berechnen:
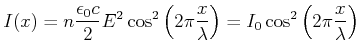 |
(5..8) |
oder umgeschrieben
![$\displaystyle I(x) = \frac{I_0}{2}\left[1+\cos\left(4\pi \frac{x}{\lambda}\right)\right]$](img750.gif) |
(5..9) |
Die Ableitung dieser Gleichung ist
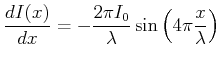 |
(5..10) |
Die maximale Steigung, also die höchste Empfindlichkeit ist
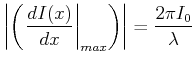 |
(5..11) |
Wir können also die Distanz
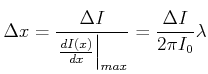 |
(5..12) |
Wenn zum Beispiel
![]() ist und
ist und
![]() ist, ist
ist, ist
![]()
(Siehe Hecht, Optik [Hec, pp. 212]) (Siehe Hecht, Optik [Hec, pp. 609]) (Siehe Pérez, Optik [Pér96, pp. 399])
|
|
![\includegraphics[width=0.9\textwidth]{stokes-reflexion-brechung}](img757.gif)
Stokessche Behandlung von Reflexion und Brechung (nach Hecht
[Hec])
|
Wir nehmen an, dass eine Welle mit der Amplitude ![]() , die vom oberen
Medium her auf die Grenzfläche auftritt, mit dem Faktor
, die vom oberen
Medium her auf die Grenzfläche auftritt, mit dem Faktor ![]() reflektiert wird,
sowie mit dem Faktor
reflektiert wird,
sowie mit dem Faktor ![]() gebrochen wird. Die Amplitude der gebrochenen Welle
ist dann
gebrochen wird. Die Amplitude der gebrochenen Welle
ist dann ![]() , die der reflektierten Welle
, die der reflektierten Welle ![]() . Das Fermatsche
Prinzip bedeutet, dass auch die zeitumgekehrte Situation eine physikalisch
realisierbare ist. Also ist auch die Strahlführung im Teilbild (b) oben eine
realisierbare Situation. Dabei müssen wir uns klar machen, dass sowohl die
einfallende Welle mit der Amplitude
. Das Fermatsche
Prinzip bedeutet, dass auch die zeitumgekehrte Situation eine physikalisch
realisierbare ist. Also ist auch die Strahlführung im Teilbild (b) oben eine
realisierbare Situation. Dabei müssen wir uns klar machen, dass sowohl die
einfallende Welle mit der Amplitude ![]() und diejenige mit
und diejenige mit ![]() eine
reflektierte und eine transmittierte, gebrochene Welle erzeugen. Dabei ist für
die Welle, die von unten kommt der Reflexionsfaktor
eine
reflektierte und eine transmittierte, gebrochene Welle erzeugen. Dabei ist für
die Welle, die von unten kommt der Reflexionsfaktor ![]() und der
Transmissionsfaktor
und der
Transmissionsfaktor ![]() . Die Situation in (c) ist nur dann äquivalent zu der
in (b), wenn gilt
. Die Situation in (c) ist nur dann äquivalent zu der
in (b), wenn gilt
| (5..13) | |||
![\includegraphics[width=0.9\textwidth]{fabry-perot-etalon}](img772.gif)
Strahlengang bei einem Fabry-Perot-Etalon (nach Hecht
[Hec] )
|
Wir betrachten nun die Reflexion an einem Etalon, also einer
Glasplatte mit dem Brechungsindex ![]() mit planparallelen Oberflächen. Im
Aussenraum sei auf beiden Seiten
mit planparallelen Oberflächen. Im
Aussenraum sei auf beiden Seiten ![]() . Die Abbildung zeigt die reflektierten
und gebrochenen Strahlen, wobei die Konvention der Gleichung (5.14)
verwendet wurde. Die reflektierten strahlen interferieren in dem weit
entfernten Punkt
. Die Abbildung zeigt die reflektierten
und gebrochenen Strahlen, wobei die Konvention der Gleichung (5.14)
verwendet wurde. Die reflektierten strahlen interferieren in dem weit
entfernten Punkt ![]() , die transmittierten Strahlen im weit entfernten Punkt
, die transmittierten Strahlen im weit entfernten Punkt
![]() . Wenn das Etalon die Dicke
. Wenn das Etalon die Dicke ![]() hat und der Winkel der Strahlen zur
Normalen im Inneren des Etalons
hat und der Winkel der Strahlen zur
Normalen im Inneren des Etalons ![]() ist, dann ist der Gangunterschied
zweier benachbarter Strahlen
ist, dann ist der Gangunterschied
zweier benachbarter Strahlen
| (5..15) |
| (5..16) |
| (5..17) |
![$\displaystyle E_{0r} =E_0\left[r-\frac{t'rt}{1-r^2}\right] = E_0 r \left(1-\frac{tt'}{1-r^2}\right)$](img782.gif) |
(5..18) |
| (5..19) |
Der zweite Spezialfall ist
![]() . Dann
sind die relativen Phasen benachbarter Wellen, unter der Berücksichtigung dass
. Dann
sind die relativen Phasen benachbarter Wellen, unter der Berücksichtigung dass
![]() und dass die innere Phase
und dass die innere Phase ![]() ist, die Phasenverschiebung
ist, die Phasenverschiebung ![]() ,
ausser bei den ersten beiden Wellen, die gleichphasig sind. Wir erhalten für
die skalare Amplitude
,
ausser bei den ersten beiden Wellen, die gleichphasig sind. Wir erhalten für
die skalare Amplitude
| (5..20) |
| (5..21) |
![$\displaystyle E_{0r}=E_0\; r\left[1+\frac{t't}{1+r^2}\right]$](img791.gif) |
(5..22) |
![$\displaystyle E_{0r}=E_0\;r\left[1+\frac{1-r^2}{1+r^2}\right]= E_0\;r\frac{1+r^2+1-r^2}{1+r^2}=E_0\frac{2r}{1+r^2}$](img793.gif) |
(5..23) |
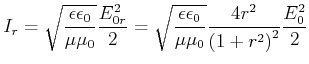 |
(5..24) |
| (5..25) | |||
| (5..26) |
| (5..27) |
| (5..28) | |||
![$\displaystyle E_0e^{i\omega t}\left\{r+t'r'te^{-i\delta}\left[1+\left(r'^2te^{-...
...^2te^{-i\delta}\right)^2+\left(r'^2te^{-i\delta}\right)^3+\ldots\right]\right\}$](img812.gif) |
![$\displaystyle \tilde{E}_r = E_0e^{i\omega t}\left[r+\frac{t'r'te^{-i\delta}}{1-r'^2e^{-i\delta}}\right]$](img814.gif) |
(5..29) |
![$\displaystyle \tilde{E}_r = E_0e^{i\omega t}\left[r-\frac{r(1-r^2)e^{-i\delta}}...
...ight]= E_0e^{i\omega t}\left[\frac{r(1-e^{-i\delta})}{1-r^2e^{-i\delta}}\right]$](img815.gif) |
(5..30) |
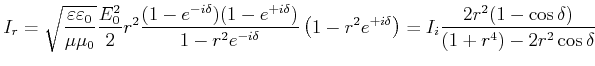 |
(5..31) |
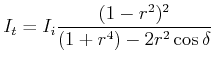 |
(5..32) |
![$\displaystyle I_i\frac{\left[\frac{2r}{1-r^2}\right]^2\sin^2(\delta/2)}{1+\left[\frac{2r}{1-r^2}\right]^2\sin^2(\delta/2)}$](img822.gif) |
(5..33) | ||
![$\displaystyle I_i \frac{1}{1+\left[\frac{2r}{1-r^2}\right]^2\sin^2(\delta/2)}$](img824.gif) |
| (5..34) |
| (5..35) |
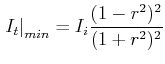 |
(5..36) |
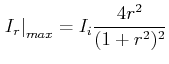 |
(5..37) |
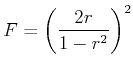 |
(5..38) |
| (5..39) | |||
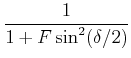 |
![\includegraphics[width=0.7\textwidth]{fabry-perot-trans}](img839.gif)
Transmission durch ein Fabry-Perot-Etalon in Abhängigkeit von der
Finesse
|
![\includegraphics[width=0.7\textwidth]{fabry-perot-refl}](img850.gif)
Reflexion an einem Fabry-Perot-Etalon in Abhängigkeit von der Finesse
|
Die Halbwertsbreite der Transmissionskurven ist durch
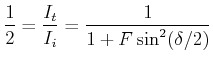 |
(5..40) |
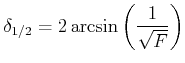 |
(5..41) |
Das Verhältnis des Abstandes benachbarter Maxima zu der Halbwertsbreite heisst Finesse und ist
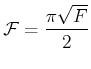 |
(5..42) |
Othmar Marti