Vektoraddition von harmonischen Wellen

(Siehe Hecht, Optik [Hec, pp. 420]) (Siehe Tipler, Physik [TM04, pp. 1120])

Wir betrachten zwei Wellen

$$E_1 = \hat E_1\sin\left(\omega t\right) \hspace{0.1\textwidth} E_2 = \hat E_2\sin\left(\omega t\right)+\delta)$$ (5..64)

Beide Schwingungen haben die gleiche Frequenz: die Zeiger der Schwingung behalten ihre relative Stellung und rotieren gemeinsam. Die Summe muss sein

$$E_1 + E_2 = \hat E_1\sin\left(\omega t\right)+\hat E_2\sin\left(\omega t\right)+\delta) = E' = \hat E' \sin\left(\omega t + \delta'\right)$$ (5..65)

Wir legen die ''1''-Achse so, dass der Vektor $E_1$ entlang dieser Achse ist. Die Komponenten von $E_2$ sind entlang der ''1''-Achse $E_{2,1} = \hat E_2\cos\delta$ und entlang der ''2''-Achse $E_{2,2} = \hat E_2\sin\delta$. Damit sind die Komponenten

$$E'_1 = \hat E_1 + \hat E_2\cos\delta$$

$$E'_2 = \hat E_2\sin\delta$$ (5..66)

Damit ist

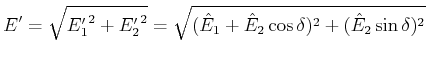$$E' = \sqrt{{E'_1}^2+{E'_2}^2} = \sqrt{(\hat E_1+\hat E_2\cos\delta)^2 +(\hat E_2\sin\delta)^2}$$ (5..67)

oder

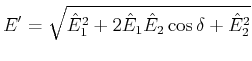$$E' = \sqrt{\hat E_1^2 + 2\hat E_1 \hat E_2 \cos\delta +\hat E_2^2}$$ (5..68)

Die Phase ist

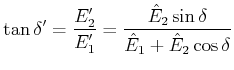$$\tan\delta' = \frac{E'_2}{E'_1} = \frac{\hat E_2\sin\delta}{\hat E_1 +\hat E_2\cos\delta}$$ (5..69)

Grafische Darstellung der Vektoraddition