Induktionsgesetz von Faraday, Integral- und Differentialform

Dieser Stoff wurde am 27. 1. 2005 behandelt

Wir betrachten die Situation in der Abbildung im Ruhesystem $S'$ der Schleife. Im Laborsystem $S$ ist das Magnetfeld

$$\vec{B}= (0;0;B)$$

in die $z$-Richtung gerichtet. Die Geschwindigkeit zeigt in die $y$-Richtung. Mit derLorentztransformation berechnen wir die Felder im System $S'$. Wir erhalten

$$\vec{B}' = (0;0;B') =(0;0;\gamma(v)\cdot B)$$ (4.304)

$$\vec{E}' = (E';0;0) = (v\cdot \gamma(v)\cdot B;0;0)$$

$$ = (v\cdot B';0;0)$$

Die Leiterschleife ist im System $S'$ in Ruhe. Also muss die EMK durch das elektrische Feld erzeugt werden.

$$U_{EMK}' = E'\cdot b = v\cdot B'\cdot b$$ (4.305)

Die Flussänderung ist

$$d\phi_B' = -B'\cdot v\cdot b\cdot dt'$$ (4.306)

Somit lauten das Induktionsgesetz und das Ohmsche Gesetz

$$U_{EMK}' = -\frac{d\phi_B'}{d t'}$$ (4.307)

$$U_{EMK}' = R\cdot I'$$

Somit gilt für die EMK die Transformation

$$U_{EMK}' = \gamma(v)U_{EMK}$$ (4.308)

Die Gleichungen (4.12) gelten in jedem Falle. Wenn $v\ll c$ ist, kann man die Unterschiede im Strom $I$, in der EMK $U_{EMK}$ und im Magnetfeld $\vec{B}$ vernachlässigen.

Die Transformationseigenschaften zeigen, dass das Induktionsgesetz auch bei stationären Leiterschleifen und zeitlich ändernden Magnetfeldern gelten muss (wir begeben uns in das System $S'$). Die Wirkung der Felder $\vec{B}$ und $\vec{E}$ sind unabhängig von ihrer Entstehung.

Versuch zur Vorlesung: Magnetische Induktion (Versuchskarte EM051)

Für einen beliebig geformten ruhenden Leiter (gegeben durch die Kurve $S$) in einem zeitlich ändernden Magnetfeld gilt für die EMK

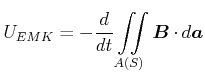$$U_{EMK} = -\frac{d}{dt}\displaystyle\iint\limits_{A(S)}^{}\vec{B}\cdot d\vec{a}$$ (4.309)

Da der Leiter in Ruhe ist, muss die EMK durch ein elektrisches Feld erzeugt sein.

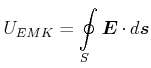$$U_{EMK} = \oint\limits_S \vec{E}\cdot d\vec{s}$$ (4.310)

Ist der Leiter nicht in Ruhe, dann ist mit Gleichung(A.40) und dem Satz von Stokes

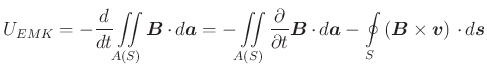$$U_{EMK} = -\frac{d}{dt}\displaystyle\iint\limits_{A(S)}^{}\vec{B}... ...cdot d\vec{a}-\oint\limits_{S} \left(\vec{B}\times\vec{v}\right) \cdot d\vec{s}$$ (4.311)

Bei einer bewegten Leiterschlaufe ist nur die EMK relevant die im mitbewegten Bezugssystem gemessen wird. Also ist dasuniverselle Induktionsgesetz von Faraday

$$\oint\limits_S \vec{E}\cdot d\vec{s}= -\displaystyle\iint\limits_{A(S)}^{}\frac{\partial}{\partial t}\vec{B}\cdot d\vec{a}$$ (4.312)

Mit dem Satz von Stokes erhält man

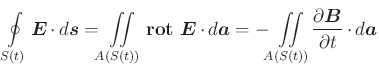$$\oint\limits_{S(t)} \vec{E}\cdot d\vec{s}= \displaystyle\iint\lim... ...style\iint\limits_{A(S(t))}^{}\frac{\partial\vec{B}}{\partial t} \cdot d\vec{a}$$ (4.313)

Für zeitunabhängige Berandungen $A(S)$ kann man auch schreiben

$$\oint\limits_{S} \vec{E}\cdot d\vec{s}= -\frac{d}{dt}\displaystyle\iint\limits_{A(S)}^{}\vec{B}\cdot d\vec{a}$$

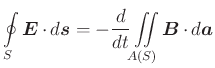Da diese Integralgleichung für beliebige Kurven $S$ gelten muss, also auch für infinitesimal kleine, erhalten wir die differentielle Form des Faradayschen Induktionsgesetzes

$${}\boldsymbol{\mathrm{rot}}{} \vec{E}= - \frac{\partial \vec{B}}{\partial t}$$ (4.314)