




Next: Vektorableitungen bei Skalarfeldern
Up: Vektoridentitšten
Previous: Produkte mit Vektoren
Contents
Index
Ableiten von Vektoren
Ableiten eines Vektors
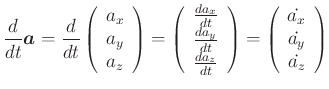 |
(A..538) |
Ableitung eines Produktes
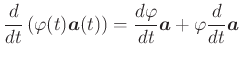 |
(A..539) |
Ableitung des Skalarproduktes
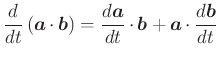 |
(A..540) |
Ableitung des Vektorproduktes
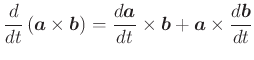 |
(A..541) |
Ableitung eines Vektors mit konstantem Betrag. Hier ist
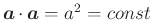 . Aus
Gleichung (A.14) folgt
. Aus
Gleichung (A.14) folgt
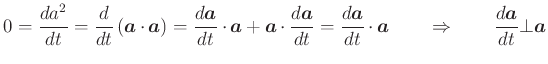 |
(A..542) |
Taylorentwicklung einer Vektorfunktion
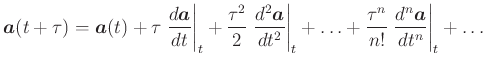 |
(A..543) |





Next: Vektorableitungen bei Skalarfeldern
Up: Vektoridentitšten
Previous: Produkte mit Vektoren
Contents
Index
Marti
2011-10-13
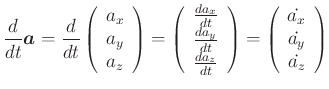

![]() . Aus
Gleichung (A.14) folgt
. Aus
Gleichung (A.14) folgt
