
Als Literatur ist für dieses Kapitel insbesondere die Werke von Haken und Wolf[HW04], von Arfken und Weber[AW95] und das Internetskript von Komma[Kom96] zu empfehlen.
Klassisch ist der Drehimpuls durch
| (6.211) |
oder in Komponenten
 |
Wir ersetzen nun
 |
||
 |
||
 |
und erhalten für die Drehimpulsoperatoren
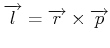 |
(6.212) | |
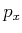 |
(6.213) | |
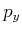 |
(6.214) |
Das Quadrat des Drehimpulses ist
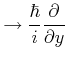 |
(6.215) |
Für Vertauschungsrelationen schreiben wir
| (6.216) |
Eine Möglichkeit diese Operatoren in Maple V zu definieren zeigt qm-defs.mws.
Wir erhalten nun die Vertauschungsrelationen
![$\displaystyle \left[\hat{\ell}_x; \hat{\ell}_y\right]$](img833.gif) |
(6.217) | |
![$\displaystyle \left[\hat{\ell}_y; \hat{\ell}_z\right]$](img835.gif) |
(6.218) | |
![$\displaystyle \left[\hat{\ell}_z; \hat{\ell}_x\right]$](img837.gif) |
(6.219) | |
![$\displaystyle \left[\hat{\ell}^2; \hat{\ell}_j\right]$](img839.gif) |
(6.220) |
Das elektrostatische Potential des Wasserstoffatoms für ein Elektron ist kugelsymmetrisch. Wir verwenden deshalb Kugelkoordinaten.
![\includegraphics[width=0.5\textwidth]{kugelkoord}](img841.gif)
Definition der Kugelkoordinaten.
|
Der Laplace-Operator in Kugelkoordinaten[BSMM00] ist
In Kugelkoordinaten sind
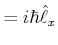 |
(6.222) | |
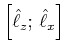 |
(6.223) | |
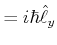 |
(6.224) | |
![$\displaystyle = -\hbar^2\left[\frac{1}{\sin^2\theta}\frac{\partial^2}{\partial ...
...l}{\partial\theta}\left(\sin\theta\frac{\partial}{\partial\theta}\right)\right]$](img849.gif) |
(6.225) |
Die Schrödingergleichung für das Wasserstoffatom ist
![$\displaystyle \left[-\frac{\hbar^2}{2m_0}\Delta +V(r)\right]\Psi=E\Psi$](img850.gif) |
(6.226) |
wobei ![]() ein allgemeines, kugelsymmetrisches Potential ist.
ein allgemeines, kugelsymmetrisches Potential ist.
Mit der Schreibweise von
![]() in Kugelkoordinaten (Gleichung (6.26) ) und Gleichung (6.22) ist
auch
in Kugelkoordinaten (Gleichung (6.26) ) und Gleichung (6.22) ist
auch
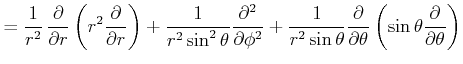 |
Wir beachten, dass Ableitungen nach einer Variablen ![]() mit Funktionen vertauschen, die nicht von
mit Funktionen vertauschen, die nicht von ![]() abhängig
sind und setzen
abhängig
sind und setzen
| (6.227) |
sowie
![$\displaystyle Y(\theta;\phi)\left[-\frac{\hbar^2}{2m_0} \frac{1}{r^2} \frac{\partial}{\partial r}\left(r^2\frac{\partial}{\partial r}\right)+V(r)\right]R(r)$](img857.gif) |
(6.228) | |
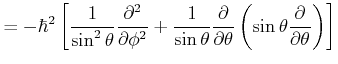 |
||
Da
![$ \left[\hat{\ell}^2;\hat{\ell}_z\right]=0$](img860.gif) ist, können die sowohl die Eigenwerte von
ist, können die sowohl die Eigenwerte von
![]() wie auch
von
wie auch
von
![]() gleichzeitig scharf gemessen werden. Mit anderen Worten, die resultierende Wellenfunktion kann
als Produkt zweier Funktionen geschrieben werden.
gleichzeitig scharf gemessen werden. Mit anderen Worten, die resultierende Wellenfunktion kann
als Produkt zweier Funktionen geschrieben werden.
Also muss man
| (6.229) | ||
| (6.230) |
Eine Mapledatei zum Berechnen der Orbitale ist hydrogen.mws. Das Original
(für eine nicht aktuelle Maple-Version ist
http://www.chemie.uni-konstanz.de/agmetz/hydrogen.mws.
Unter der Annahme, dass ![]() bekannt ist, wird die Gleichung für den Radialteil
bekannt ist, wird die Gleichung für den Radialteil
![$\displaystyle \left[ -\frac{\hbar^{2}}{2m_{0}}\frac{1}{r^{2}}\frac{\partial}{\p...
...{\hbar^{2}\omega}{2m_{0}r^{2}}\right] R\left( r\right) =E\cdot R\left( r\right)$](img867.gif) |
(6.231) |
nach Arfken und Weber[AW95, 736] schreibt man
| (6.232) |
Aus
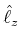 |
||
| (6.233) | ||
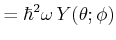 |
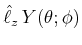 |
|
| (6.234) |
berechnet man für den azimutalen Anteil:
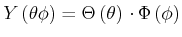 |
(6.235) |
Die Lösung der Gleichung ist
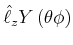 |
(6.236) |
Dies sind orthogonale Funktionen, da
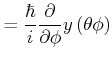 |
(6.237) |
Damit
![]() , die Observable, eindeutig bestimmt ist auf den Intervall
, die Observable, eindeutig bestimmt ist auf den Intervall
![]() muss
muss
![]() ganzzahlig sein.
ganzzahlig sein.
Für ![]() bekommt man
bekommt man
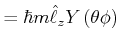 |
(6.238) | |||
| (6.239) |
Subtrahieren ergibt
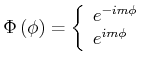 |
(6.240) |
Bezeichnungswechsel
| (6.241) |
Um eine Beziehung zwischen ![]() und
und ![]() zu bekommen multiplizieren wir von links mit
zu bekommen multiplizieren wir von links mit
![]()
| (6.242) |
Nach Haken, Wolf[HW04] ergibt das Integral über ![]() und
und ![]() , dass
, dass
| (6.243) |
sein muss.
Mit
| (6.244) |
kann man die Operatoren
| (6.245) | ||
| (6.246) |
definieren.
Es ist
| (6.247) |
es gilt
| (6.248) | ||
| (6.249) |
Wir setzen
![]() ein
ein
| (6.250) |
![]() sind vertauschbar
sind vertauschbar
| (6.251) |
d.h. wenn
![]() eine Eigenfunktion ist, dann ist auch
eine Eigenfunktion ist, dann ist auch
![]() eine Eigenfunktion
eine Eigenfunktion
Aus der Azimutalgleichung erhalten wir
| (6.252) |
| (6.253) | ||
| (6.254) |
also
| (6.255) |
| (6.256) |
Damit ist auch
![]() eine Eigenfunktion zur Azimutalgleichung, aber mit anderem Eigenwert.
eine Eigenfunktion zur Azimutalgleichung, aber mit anderem Eigenwert.
| (6.257) |
Die folgende Relation gilt
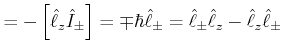 |
||
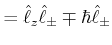 |
||
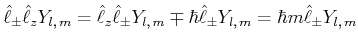 |
||
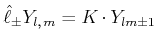 |
(6.258) |
Da
![]() sein muss, gilt auch
sein muss, gilt auch
| (6.259) | ||
| (6.260) | ||
| (6.261) | ||
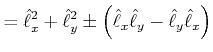 |
||
da
| (6.262) |
Aus
| (6.263) |
| (6.264) |
Nach
![]() aufgelöst
aufgelöst
| (6.265) | ||
| (6.266) | ||
| 0 | (6.267) |
Da
![]() ist, folgt
ist, folgt
![]()
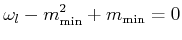 |
(6.268) |
Da die Funktion eindeutig sein muss, muss ![]() eine ganze Zahl sein.
eine ganze Zahl sein.
Wir definieren: ![]()
| (6.269) |
mit
| (6.270) | ||
| (6.271) |
also ist
| (6.272) | ||
| (6.273) |
und
| (6.274) |
mit der Normierung
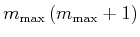 |
(6.275) |
Wir wissen schon, dass
| (6.276) |
es ist
| (6.277) |
Wir wollen
| (6.278) |
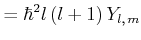 |
||
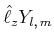 |
||
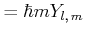 |
||
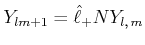 |
||
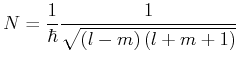 |
||
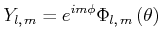 |
||
![$\displaystyle =\hbar\left( \pm\cos\phi+i\sin\phi\right) \left[ \frac{\partial }{\partial\theta}\pm i\cot\theta\frac{\partial}{\partial\phi}\right]$](img968.gif) |
||
![$\displaystyle =\hbar\left( \pm\frac{e^{i\phi}+e^{-i\phi}}{2}+\frac{i\left( e^{i...
...ac{\partial}{\partial\theta}\pm i\cot\theta\frac{\partial}{\partial\phi}\right]$](img969.gif) |
||
![$\displaystyle =\pm\hbar e^{\pm i\phi}\left[ \frac{\partial}{\partial\theta}\pm i\cot\theta\frac{\partial}{\partial\phi}\right]$](img970.gif) |
Wir setzen in die beiden Relationen für
![]() und
und
![]() die Funktion
die Funktion
![]() ein und erhalten
ein und erhalten
![$\displaystyle = \hbar e^{i\phi}\left[ \frac{\partial}{\partial\theta}-m\cot\theta \frac{\partial}{\partial\phi}\right]$](img975.gif) |
(6.279) | |
![$\displaystyle = -\hbar e^{-i\phi}\left[ \frac{\partial}{\partial\theta}+ m\cot\theta \frac{\partial}{\partial\phi}\right]$](img977.gif) |
(6.280) |
Für ![]() wird
wird
![]()
| 0 | ||
![$\displaystyle =-\hbar e^{-i\phi}e^{-il\phi}\left[ \frac{\hbar\Theta e}{\hbar\theta} -i\cot\theta\left( -il\right) \Theta_{e}\right]$](img981.gif) |
||
![$\displaystyle =-\hbar e^{-i\phi}e^{-il\phi}\left[ \frac{\partial}{\partial\theta} -l\cot\theta\right] \Theta_{l}$](img982.gif) |
also bekommen wir die Differentialgleichung
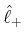 |
(6.281) |
Deren Lösung ist
| (6.282) |
aus
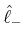 |
(6.283) |
bekommt man
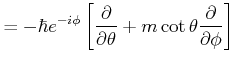 |
(6.284) |
Mit
![$\displaystyle \hat{\ell}_{+}Y_{l\text{,} m}=\hbar e^{i\phi}\left[ \frac{\partial}{\partial\theta }-m\cot\theta\right] Y_{l\text{,} m}$](img987.gif) |
(6.285) |
kann man alle Funktionen konstruieren
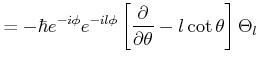 |
(6.286) | |||||
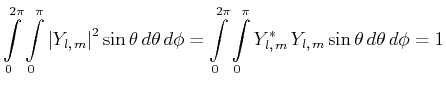 |
(6.287) | |||||
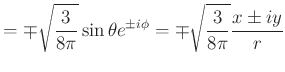 |
(6.288) | |||||
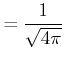 |
(6.289) | |||||
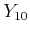 |
(6.290) | |||||
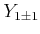 |
(6.291) |
Plots dieser Wellenfunktionen finden Sie im Anhang A.1.
![$\displaystyle \left[ -\frac{\hbar^{2}}{2m_{0}}\frac{1}{r^{2}}\frac{d}{dr}\left(...
...m_{0}r^{2} }+V\left( v\right) \right] R\left( r\right) =E\cdot R\left( r\right)$](img1006.gif) |
(6.292) |
Wir verwenden
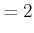 |
(6.293) |
und Multiplizieren die Gleichung mit
![]()
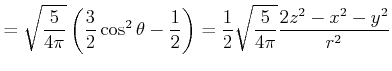 |
(6.294) |
wir setzen
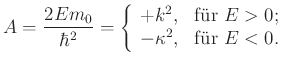 |
(6.295) |
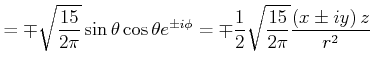 |
(6.296) |
![$\displaystyle \frac{d^{2}R}{dr^{2}}+\frac{2}{r}\frac{dR}{dr}+\left[ A-\widetilde{V}\left( r\right) -\frac{l\left( l+1\right) }{r^{2}}\right] R=0$](img1012.gif) |
(6.297) |
Wir betrachten den Grenzfall:
![]() und verwenden den Ansatz
und verwenden den Ansatz
![]() .
Für die Ableitungen gilt
.
Für die Ableitungen gilt
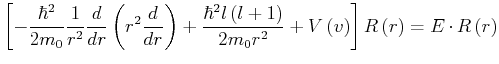 |
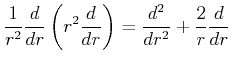 |
|
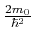 |
||
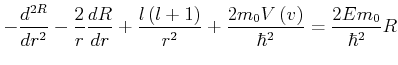 |
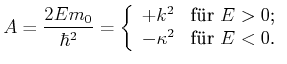 |
|
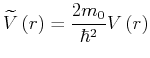 |
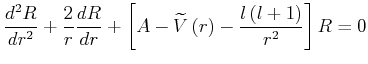 |
![$\displaystyle \frac{1}{r}\frac{d^{2}u}{dr^{2}}+\left[ A-\widetilde{V}\left( r\right) -\frac{l\left( l+1\right) }{r^{2}}\right] \frac{u}{r}$](img1022.gif) |
(6.298) |
oder mit ![]()
![$\displaystyle \frac{d^{2}u}{dr^{2}}+\left[ A-\widetilde{V}\left( r\right) -\frac{l\left( l+1\right) }{r^{2}}\right] u=0$](img1024.gif) |
(6.299) |
Im Grenzfall ![]() gilt
gilt
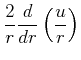 |
Wir erhalten in diesem Grenzfall
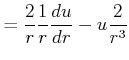 |
(6.300) |
Für die beiden Fälle ![]() und
und ![]() die folgenden Lösungen:
die folgenden Lösungen:
|
||||||||||
|
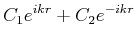 |
(6.305) |
Variablentransformation
| (6.306) |
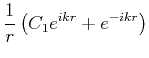 |
(6.307) |
| (6.308) |
mit
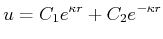 |
||
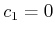 |
wird
| 0 | ![$\displaystyle =\frac{d^{2}\widetilde{R}}{d\rho^{2}}4\kappa^{2}+\frac{4\kappa}{\...
...2} 4\pi\epsilon_{0}\rho}-\frac{l\left( l+1\right) 4\kappa^{2}}{\rho^{2}}\right]$](img1050.gif) |
|
| 0 | ![$\displaystyle = \frac{d^{2}\widetilde{R}}{d\rho^{2}}+\frac{2}{\rho}\frac{d\wide...
...r^{2} 4\pi\epsilon_{0}2\kappa \rho}-\frac{l\left( l+1\right) }{\rho^{2}}\right]$](img1051.gif) |
|
![$\displaystyle =\frac{d^{2}\widetilde{R}}{d\rho^{2}}+\frac{2}{\rho}\frac{d\widet...
...frac{B}{\kappa\rho}-\frac{l\left( l+1\right) }{\rho^{2}}\right]\widetilde{R} =0$](img1052.gif) |
mit
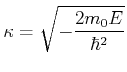 |
(6.309) |
Exponentialansatz
| (6.310) |
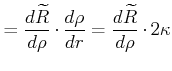 |
||
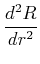 |
||
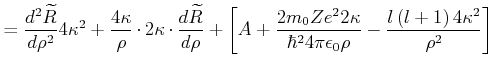 |
||
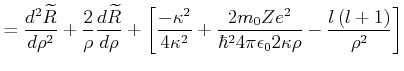 |
||
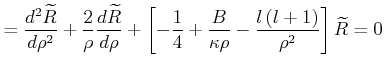 |
![$\displaystyle =e^{-\rho/2}\left[ \frac{ v }{4}-\frac{1}{2}\frac{d v }{d\rho}-\f...
...{d^{2} v }{d\rho^{2}}-\frac{ v }{\rho}+\frac{2}{\rho }\frac{d v }{d\rho}\right]$](img1062.gif) |
|
![$\displaystyle =e^{-\rho/2}\left[ \frac{ v }{4}-\frac{ v }{\rho}+\frac{d v }{d\rho }\left( \frac{2}{\rho}-1\right) +\frac{d^{2} v }{d\rho_{2}}\right]$](img1063.gif) |
||
![$\displaystyle =\frac{e^{-\rho/2}}{4\rho}\left[ v \left( \rho-4\right) +\frac{d v }{d\rho}\left( -4\rho+8\right) +4\rho\frac{d^{2} v }{d\rho^{2}}\right]$](img1064.gif) |
wir spalten
![]() ab.
ab.
![$\displaystyle \frac{d^{2}v}{d\rho^{2}}+\left( \frac{2}{\rho}-1\right) \frac{dv}...
...rho}-\frac{1}{4}+\frac{B}{k\rho} -\frac{l\left( l+1\right) }{\rho^{2}}\right] v$](img1066.gif) |
||
![$\displaystyle \frac{d^{2}v}{d\rho^{2}}+\left( \frac{2}{\rho}-1\right) \frac{dv}...
...}{\rho}\left( \frac{B}{K}-1\right) -\frac{l\left( l+1\right) }{\rho^{2}}\right]$](img1067.gif) |
Rekursionsansatz
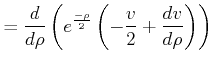 |
(6.311) |
einsetzen ergibt
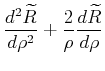 |
||
![$\displaystyle +\left[ \left( \frac{B}{k}-1\right) \frac{1}{\rho}+\frac{l\left( ...
...ght) }{\rho^{2}}\right] \sum\limits_{\nu=0}^{\infty} \alpha_{\nu}\rho^{\nu+\mu}$](img1071.gif) |
niedrigster Exponent ist ![]() , also
, also ![]()
| (6.312) |
und damit
Lösungen
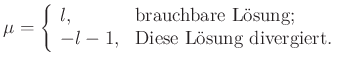 |
Durch Berechnung der höheren Potenzen erhält man
 |
(6.313) |
mit
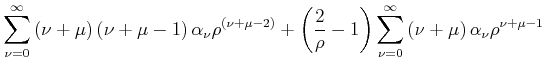 |
(6.314) |
wobei ![]() durch
durch ![]() ersetzt wurde, da
ersetzt wurde, da ![]() von
von ![]() abhängt.
abhängt.
2 Lösungstypen:
Mit ![]() folgt
folgt ![]()
Wir berechnen die ersten
![]() und setzen
und setzen
![]() ;
;
| 0 | 0 | 0 | 0 | |||||||
| 0 |
|
0 |
|
0 |
|
|
|
0 | ||
| 0 | 0 | 0 |
|
0 | 0 |
|
|
0 | 0 | |
| 0 | 0 | 0 | 0 | 0 | 0 |
|
0 | 0 | 0 | |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
Dabei ist
![]() : Hauptquantenzahl
: Hauptquantenzahl
![]() : Drehimpulsquantenzahl
: Drehimpulsquantenzahl
Die dazugehörige nicht normierte Funktion lautet also
 |
(6.315) |
|
|
||
| 0 |
|
|
| 0 |
|
|
|
|
||
| 0 |
|
|
|
|
||
| 2 |
|
|
| 0 |
|
|
|
|
||
|
|
||
|
|
Also ist
|
|
||
| 0 |
|
|
| 0 |
|
|
|
|
||
| 0 |
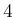 |
|
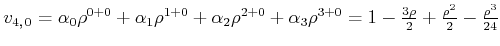 |
||
| 2 |
|
|
| 0 |
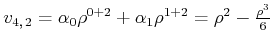 |
|
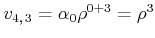 |
||
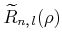 |
||
|
|
und schliesslich mit
![]()
|
|
||
| 0 |
|
|
| 0 |
|
|
|
|
||
| 0 |
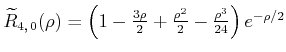 |
|
|
|
||
| 2 |
|
|
| 0 |
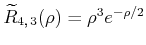 |
|
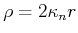 |
||
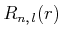 |
||
|
|
wobei
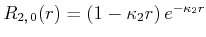 |
ist. Der Energieeigenwert ist weiter
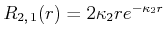 |
(6.316) |
so dass
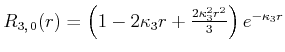 |
und
| (6.317) |
ist.
Der Bohrsche Radius ![]() wird aus
wird aus
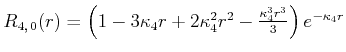
berechnet
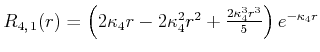 |
(6.318) |
Die normierten Funktionen sind also
|
|
||
| 0 |
|
|
| 0 |
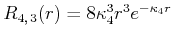 |
|
|
|
||
| 0 |
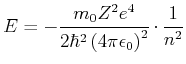 |
|
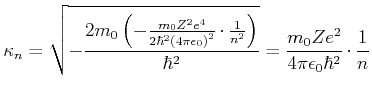 |
||
| 2 |
|
|
| 0 |
 |
|
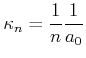 |
||
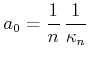 |
||
|
|
Bei Hyperphysics gibt es eine schöne Darstellung dieser Funktionen. Eine Skizze dieser Wellenfunktionen findet sich auch im Anhang A.2.
| (6.319) |
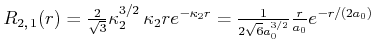 inverser Radius inverser Radius |
(6.320) |
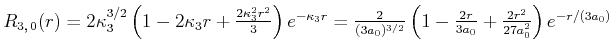 |
(6.321) |
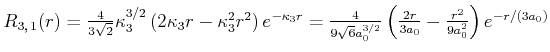 |
(6.322) |
also ist
| (6.323) |
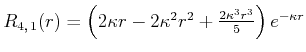 |
Die Wellenfunktion ist dann
wobei
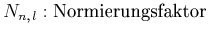 der Bohr-Radius der Bohr-Radius |
(6.325) | |
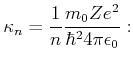 |
(6.326) |
Also lauten die Wasserstofforbitale[AW95]
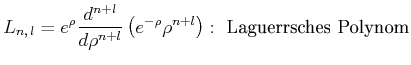 |
||
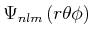 |
||
|
|
|
|
Die folgende Ausarbeitung folgt der Behandlung von Gordon Baym[Bay69, 66]. Eine analoge Darstellung findet sich im Buch von landau und Lifschitz [LL79, 46]
Seien
![]() und
und
![]() normierte Wellenfunktionen.
normierte Wellenfunktionen.
Behauptung:
Beweis:
Sei
Dann ist
| 0 | ||
| (6.328) |
Gleichheit gilt also nur wenn
![]()
Wir wählen das beliebige ![]() so, dass
so, dass
und setzen in Gleichung (6.131) ein
Bei nicht normierten Funktionen verwendet man
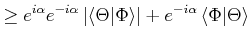 und und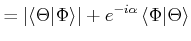 |
Aus Gleichung (6.130) bekommt man
Aus Gleichung (6.131) erhält man
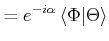 |
||
und damit
Wir erhalten für die Wellenfunktion
![]() für die Standardabweichungen
für die Standardabweichungen
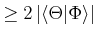 |
(6.331) | |
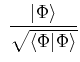 |
(6.332) |
wobei für die Erwartungswerte wie üblich gilt:
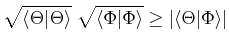 |
Wir nehmen an, dass das zu untersuchende Teilchen die Wellenfunktion
![]() hat. Wir definieren
hat. Wir definieren
| (6.333) | ||
| (6.334) |
Dann ist
| (6.335) | |||
| (6.336) |
Aus Gleichung (6.133) erhält man mit
![]()
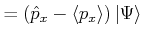 |
||
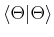 |
||
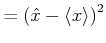 |
||
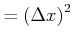 |
||
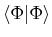 |
||
![$\displaystyle =-\frac{i}{2}\left<{\Psi}\right\vert\left[\hat{x}\text{,} \hat{p}_x\right]\left\vert{\Psi}\right>$](img1229.gif) |
||
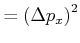 |
||
Unter der Annahme dass
![]() und
und
![]() , was sich immer durch eine
Galilei-Transformation erreichen lässt.
, was sich immer durch eine
Galilei-Transformation erreichen lässt.
Wir haben bei der Berechnung nichts über die Operatoren ![]() und
und ![]() angenommen, so dass auch für
allgemeine Operatoren
angenommen, so dass auch für
allgemeine Operatoren
![]() und
und
![]() , bei denen man über eine Transformation
, bei denen man über eine Transformation
![]() und
und
![]() erreichen kann, für die Unbestimmtheitsrelation gilt
erreichen kann, für die Unbestimmtheitsrelation gilt
|
Nach Landau und Lifschitz [LL79, 46] folgt aus
| (6.338) |
wobei ![]() und
und ![]() beliebige Operatoren zu den klassischen Grössen
beliebige Operatoren zu den klassischen Grössen ![]() und
und ![]() sind und bei der
sind und bei der
![]() der Operator zur klassischen Grösse
der Operator zur klassischen Grösse ![]() (der Poisson-Klammer) ist, dass im klassischen Grenzfall alle
Operatoren vertauschbar sind. In zweiter Näherung kann der Operator
(der Poisson-Klammer) ist, dass im klassischen Grenzfall alle
Operatoren vertauschbar sind. In zweiter Näherung kann der Operator ![]() als Multiplikation mit
als Multiplikation mit ![]() auffassen, so dass
auffassen, so dass
| (6.339) |
und in Analogie zu den Impulsen
| (6.340) |
3 Quantenzahlen
| 0 | ||
Diese drei Quantenzahlen beschreiben den atomaren Zustand
Rydberg-Gesetz: nur ![]() ist wichtig
ist wichtig
![]() alle
alle ![]() - und
- und ![]() -Zustände haben die gleiche Energie
-Zustände haben die gleiche Energie
![]() Entartung
Entartung
Fragen: in welcher Reihenfolge werden die Zustände besetzt?
- Wird die Entartung aufgehoben?
- Grund für die Entartung
- Kepler-Gesetze beschreiben geschlossene Planetenbahnen, wenn das Potential sich wie ![]() verhält.
verhält.
Abweichungen vom
![]() -Gesetz bedeutet Perihel-Drehung.
-Gesetz bedeutet Perihel-Drehung.
![\includegraphics[width=0.7\textwidth]{Quantenzahle-6-3-3-001}](img1254.gif)
Sommerfeld-Bild
|
Modell eines Atoms mit einem Leuchtelektron
![\includegraphics[width=0.7\textwidth]{Quantenzahle-6-3-3-002}](img1255.gif)
Atom mit einem Leuchtelektron
|
für
![]() gilt
gilt
![]() unabhängig vom inneren Aufbau
unabhängig vom inneren Aufbau
für
![]() muss
muss
![]()
![\includegraphics[width=0.5\textwidth]{Quantenzahle-6-3-3-003}](img1259.gif)
Coulombpotential und effektives Potential
|
![]() Innen ist das
Innen ist das ![]() auf einer anderen Bahn als aussen
auf einer anderen Bahn als aussen
![]() andere Energie: Energieentartung aufgehoben.
andere Energie: Energieentartung aufgehoben.
Grotrian-Diagramm
![\includegraphics[width=0.7\textwidth]{grotman}](img1261.gif)
Grotrian-Diagramm für Litium
|
![\begin{displaymath}\begin{array}[c]{rrr}s & l=0 & \text{sharp}\\
p & l=1 & \te...
...f & l=3 & \text{fundamental}\\
g & l=4 & \text{:}\end{array} \end{displaymath}](img1262.gif)
grosse Buchstaben: bezieht sich auf das gesamte System
kleine Buchstaben: bezieht sich auf ein Elektron
Für die Energien gilt:
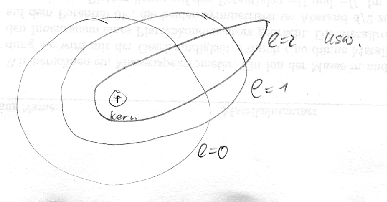
![]() Hauptserie
Hauptserie
![]()
Nebenserien
![]()
![]()
![]()
Elektronenkonfiguration
![]() Argon-Konfiguration
Argon-Konfiguration
Beispiel: K-Atom +1![]()
Argon
![]() oder
oder
![]()
ist der nächste Zustand ein ![]() oder
oder ![]()
![]() -Elektronen sind näher am Kern als
-Elektronen sind näher am Kern als ![]() -Elektronen
-Elektronen
Abschirmung?
![]() kommt zeitweise näher an Kern (unabgeschirmt)
kommt zeitweise näher an Kern (unabgeschirmt)
![]() Zustand ist niedriger als
Zustand ist niedriger als ![]()
![\includegraphics[width=0.7\textwidth]{quantenzahle-6-3-3-005}](img1276.gif)
Radiale Wellenfunktionen des Wasserstoffatoms
|
