
Weiter: Mechanische Maschinen Oben: Mechanik starrer Körper Zurück: Der starre Rotator Skript: PDF-Datei Übungen: Blätter ILIAS: Materialien Korrekturen
| Definition: Ein Kreisel ist ein starrer Körper, dessen Bewegung durch einen Fixpunkt festgelegt ist. |
|
|
Die Lage der Drehachse eines Kreisels hängt von der Zeit ab
| (6.588) |
![\includegraphics[width=0.4\textwidth]{starr-018}](img2296.gif)
Kreisel
|
Die Geschwindigkeit eines Massenelementes
![]() ist gegeben durch
ist gegeben durch
| (6.589) |
![]() ist die momentane Geschwindigkeit von
ist die momentane Geschwindigkeit von
![]() .
.
Die momentane Drehachse ![]() bewegt sich im Raum entlang einer Kegeloberfläche, der Oberfläche des
festen Polkegels
bewegt sich im Raum entlang einer Kegeloberfläche, der Oberfläche des
festen Polkegels ![]() .
.
![\includegraphics[width=0.2\textwidth]{starr-019}](img2299.gif)
Polkegel
|
Bezüglich des Körpers bewegt sich ![]() auf einen beweglichen Polkegel
auf einen beweglichen Polkegel ![]() .
.
![]() (körperfest) rollt auf
(körperfest) rollt auf ![]() ab. Die Berührungslinie der beiden Polkegel ist die momentane Drehachse.
ab. Die Berührungslinie der beiden Polkegel ist die momentane Drehachse.
Wir betrachten den Zusammenhang zwischen
![]() und
und
![]() im
körperfesten Bezugssystem.
im
körperfesten Bezugssystem.
| (6.590) |
oder
| (6.591) |
oder
![]() .
.
![]() heisst der Trägheitstensor des Kreisels (des
starren Rotators) bezüglich dem Fixpunkt 0. Die Komponenten von
heisst der Trägheitstensor des Kreisels (des
starren Rotators) bezüglich dem Fixpunkt 0. Die Komponenten von
![]() sind
sind
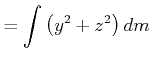 |
||
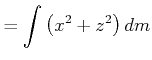 |
||
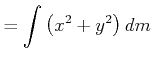 |
(6.592) | |
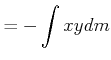 |
||
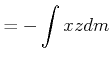 |
||
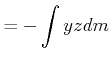 |
(6.593) |
![]() ist symmetrisch, das heisst
ist symmetrisch, das heisst
![]()
Beweis: Die Definition des Drehimpulses ist
Für ein Massenelement ![]() gilt
gilt
Mit
![]() wird
wird
Also wird
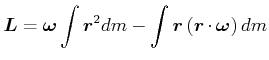 |
(6.594) |
![\begin{displaymath}\vec{r}=\left(
\begin{array}[c]{c}
x\\
y\\
z
\end{array}\right) \end{displaymath}](img2331.gif) und betrachten die
und betrachten die 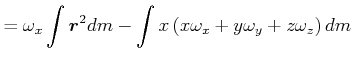 |
||
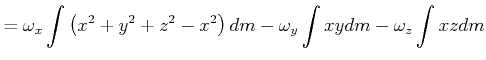 |
(6.595) |
also ist
![]() und
und
![]() und
und
![]() , wie
behauptet.
, wie
behauptet.
Die Grösse
![]() heisst Deviationsmoment.
heisst Deviationsmoment.
Die Spur von
![]() ändert sich nicht bei einer Drehung des Koordinatensystems
ändert sich nicht bei einer Drehung des Koordinatensystems
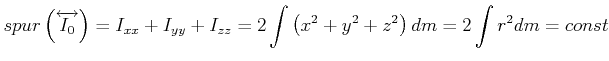 |
(6.596) |
Weiter gilt
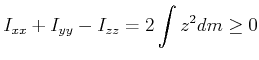 |
(6.597) |
und zyklisch.
Frage: gibt es ein Koordinatensystem, in dem die Deviationsmomente verschwinden?
Diese Frage ist äquivalent zur Frage nach den Eigenvektoren einer Matrix.
Aus der Mathematik weiss man, dass, da
![]() gilt, ein
Hauptachsensystem existiert, in dem
gilt, ein
Hauptachsensystem existiert, in dem
![]() diagonal ist.
diagonal ist.
Wir nennen die Hauptträgheitsmomente:
![]()
Seien
![]() ,
,
![]() ,
,
![]() körperfeste Basisvektoren, die so nummeriert werden, dass
körperfeste Basisvektoren, die so nummeriert werden, dass
![]() ist.
ist.
Sei
![]() die momentane Drehachse und
die momentane Drehachse und
![]() die momentane Winkelgeschwindigkeit. Dann gilt
die momentane Winkelgeschwindigkeit. Dann gilt
Der Drehimpulsvektor entlang der ![]() -Achse ist dann
-Achse ist dann
| (6.599) |
Die Spur des Trägheitstensors ist
![]() .
.
Es gilt
![]() , da der Kreisel ein starrer Rotator ist. Im
Hauptachsensystem haben wir
, da der Kreisel ein starrer Rotator ist. Im
Hauptachsensystem haben wir
Beweis
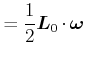 |
||
![$\displaystyle =\frac{1}{2}\left( \begin{array}[c]{c} I_{x}\omega_{x} I_{y}\om...
...t( \begin{array}[c]{c} \omega_{x} \omega_{y} \omega_{z} \end{array} \right)$](img2353.gif) |
||
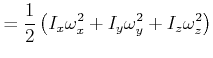 |
||
![$\displaystyle =\frac{1}{2}\left( \begin{array}[c]{c} L_{x} L_{y} L_{z} \end...
...c{L_{x}}{I_{x}} \frac{L_{y}}{I_{y}} \frac{L_{z}}{I_{z}} \end{array} \right)$](img2355.gif) |
||
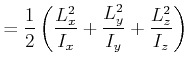 |
Die momentane Drehachse ist durch
![]() gegeben. Wir definieren die
momentane Drehachse durch einen zeitabhängigen Einheitsvektor
gegeben. Wir definieren die
momentane Drehachse durch einen zeitabhängigen Einheitsvektor
![]() mit
mit
![]() . Dann ist
. Dann ist
Durch Umstellen erhalten wir
wobei wir
gesetzt haben. ![]() ist das Trägheitsmoment bezüglich der momentanen Drehachse
ist das Trägheitsmoment bezüglich der momentanen Drehachse ![]() . Wenn die
kinetische Energie des Kreisels erhalten ist, ist auch
. Wenn die
kinetische Energie des Kreisels erhalten ist, ist auch ![]() eine Konstante.
eine Konstante.
|
|
Wir möchten den Körper mit einer allgemeinen Form, der durch den
Trägheitstensor
![]() charakterisiert ist, durch den
einfachst möglichen Körper mit den gleichen Rotationseigenschaften ersetzen.
Dies ist das Trägheitsellipsoid charakterisiert durch den Vektor
charakterisiert ist, durch den
einfachst möglichen Körper mit den gleichen Rotationseigenschaften ersetzen.
Dies ist das Trägheitsellipsoid charakterisiert durch den Vektor ![]() . Wir
verwenden zur Definition von
. Wir
verwenden zur Definition von ![]() die Definition des Trägheitsmomentes
die Definition des Trägheitsmomentes ![]() bezüglich der momentanen Drehachse
bezüglich der momentanen Drehachse ![]() vom vorherigen Abschnitt.
vom vorherigen Abschnitt.
![$\displaystyle \vec{u}=\left( \begin{array}[c]{c} u_{x} u_{y} u_{z} \end{a...
...ft( \frac{e_{x}}{\sqrt{I}},\frac{e_{y}}{\sqrt{I}},\frac{e_{z}}{\sqrt{I}}\right)$](img2368.gif) |
(6.604) |
Wir setzen ![]() in die Ellipsengleichung ein und erhalten
in die Ellipsengleichung ein und erhalten
![]() beschreibt also in der Tat die Oberfläche eines Ellipsoids, das wir Trägheitsellipsoid nennen. Aus der
Konstruktion folgen die Eigenschaften des Trägheitsellipsoides:
beschreibt also in der Tat die Oberfläche eines Ellipsoids, das wir Trägheitsellipsoid nennen. Aus der
Konstruktion folgen die Eigenschaften des Trägheitsellipsoides:
Aus Gleichung (6.84) folgt, dass die Längen der Halbachsen des Trägheitsellipsoides
![]() ,
,
![]() und
und
![]() sind.
sind.
Für einen allgemeinen Kreisel mit dem Fixpunkt 0 im Schwerpunkt ![]() gibt es die folgenden Beziehungen zwischen
den Hauptträgheitsmomenten:
gibt es die folgenden Beziehungen zwischen
den Hauptträgheitsmomenten:
Bemerkung: nur Rotationen eines freien Körpers um die Hauptachsen mit dem grössten und dem kleinsten Hauptträgheitsmoment sind stabil.
|
Definition: Ein Kreisel heisst kräftefrei, wenn |
Dann ist
und
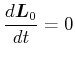
d.h.
Die kinetische Energie ist dann
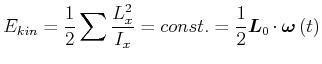 |
(6.606) |
d.h.
![]() bewegt sich auf einem Kegel um
bewegt sich auf einem Kegel um
![]()
Wie realisiert man einen kräftefreien Kreisel?
![\includegraphics[width=0.2\textwidth]{starr-020}](img2388.gif)
Kräftefreier Kreisel
|
Es ist
d.h.
![]() . Dabei ist
. Dabei ist
![]() die Projektion von
die Projektion von
![]() auf
auf
![]() . Es gibt zwei
Fälle:
. Es gibt zwei
Fälle:
Bei einer permanenten Rotation ist
![]() wenn
wenn
![]() zur Hauptachse
ist. Es gilt dann
zur Hauptachse
ist. Es gilt dann
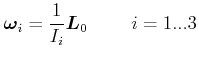
Beim asymmetrischen Kreisel ist
Rotationen um
Nach Gleichung (6.78) und Gleichung (6.80) ist
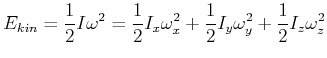
wenn
![]() die Kreisfrequenz im Hauptachsensystem ist. Da
die Kreisfrequenz im Hauptachsensystem ist. Da
![]() ist, sind alle einzelnen Komponenten kleiner als
ist, sind alle einzelnen Komponenten kleiner als ![]() . Also kann
man schreiben
. Also kann
man schreiben
![\includegraphics[width=0.4\textwidth]{starr-021}](img2420.gif)
Poinsotsche Konstruktion
|
Die Zeichnung zeigt, dass damit auch
![]() und damit
und damit
![]() ist. Weiter ist nach Gleichung (6.79)
ist. Weiter ist nach Gleichung (6.79)
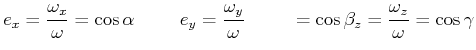
Nach Gleichung (6.82) ist
Wir setzen den Punkt ![]() im Abstand
im Abstand
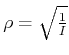 (siehe Gleichung (6.82) ) vom Nullpunkt auf die
Drehachse. Mit
(siehe Gleichung (6.82) ) vom Nullpunkt auf die
Drehachse. Mit
![\begin{displaymath}Q=\left(
\begin{array}[c]{c}
x\\
y\\
z
\end{array}\right) =\vec{\rho}\end{displaymath}](img2427.gif) wird
wird
Diese Gleichung beschreibt also nichts anderes als das Trägheitsellipsoid.
Allgemein gilt, dass eine Funktion
![]() eine Oberfläche beschreibt. Dann ist der
Normalenvektor der Funktion
eine Oberfläche beschreibt. Dann ist der
Normalenvektor der Funktion
![]() ,
,![]() ,
,![]() durch
durch
| (6.608) |
Beweis:
Wir betrachten das totale Differential ![]() . Dieses muss null sein, da die Funktion
. Dieses muss null sein, da die Funktion
![]() eine Konstante
ist. Wir bekommen also
eine Konstante
ist. Wir bekommen also
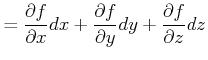 |
||
| (6.609) | ||
| (6.610) |
Damit ist
![]() senkrecht zu
senkrecht zu
![]() . Da
. Da
![]() in der Fläche
in der Fläche
![]() liegt (Die
möglichen Änderungen von
liegt (Die
möglichen Änderungen von
![]() sind durch die durch
sind durch die durch
![]() beschriebene Fläche begrenzt) ist
beschriebene Fläche begrenzt) ist
![]() senkrecht zur Tangentialebene und damit der Normalenvektor.
senkrecht zur Tangentialebene und damit der Normalenvektor.
|
Der Normalenvektor zum Trägheitsellipsoid
|
Im Hauptachsensystem ist
Von der Konstruktion her sind
![]() und
und
![]() parallel. Wir können wie folgt umformen
parallel. Wir können wie folgt umformen
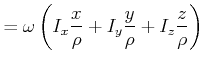 |
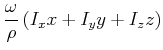 |
|||
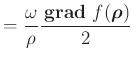 |
Deshalb ist
![]() , das heisst, dass
, das heisst, dass ![]() senkrecht zur Tangentialebene
senkrecht zur Tangentialebene
![]() im Durchstosspunkt
im Durchstosspunkt ![]() von
von
![]() durch das Trägheitsellipsoid ist.
durch das Trägheitsellipsoid ist.
![\includegraphics[width=0.4\textwidth]{starr-022}](img2459.gif)
Trägheitsellipsoid
|
Rezept zur Konstruktion von ![]() :
:
![\includegraphics[width=0.4\textwidth]{starr-023}](img2460.gif)
Interpretation der Poinsotschen Konstruktion
|
Wir bezeichnen mit ![]() den Abstand von 0 zur Tangentialebene
den Abstand von 0 zur Tangentialebene ![]() in
in ![]() . Der Abstand
. Der Abstand ![]() hat die
folgende Bedeutung
hat die
folgende Bedeutung
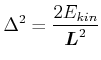 |
(6.611) |
Beweis: Die Tangentialebene ![]() ist durch den Vektor
ist durch den Vektor
![]() ,
,![]() ,
,![]() gegeben. Dann gilt
gegeben. Dann gilt
| (6.612) |
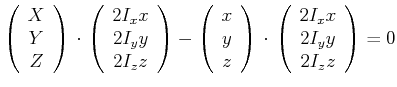
Ausmultipliziert erhält man
Wir bezeichnen mit
![]() den Einheitsvektor entlang
den Einheitsvektor entlang
![]() . Dann ist
. Dann ist ![]()
| (6.614) |
oder
Wir vergleichen Gleichung (6.92) und Gleichung (6.94) . Die Vorfaktoren von ![]() ,
, ![]() und
und ![]() müssen identisch sein, da
bei beliebiger Variation der drei Grössen beide Gleichungen konstant sein müssen. Insbesondere kann man
müssen identisch sein, da
bei beliebiger Variation der drei Grössen beide Gleichungen konstant sein müssen. Insbesondere kann man ![]() setzen und bekommt dann
setzen und bekommt dann
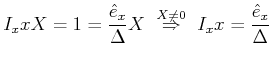
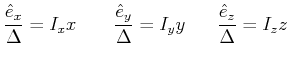 |
(6.616) |
| (6.617) |
Da
![]() ein Einheitsvektor ist, gilt
ein Einheitsvektor ist, gilt
| (6.618) |
![]() und
und
![]() sind parallel, also ist
sind parallel, also ist
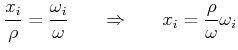 |
(6.619) |
und
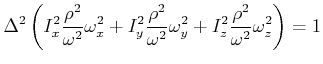 |
(6.620) |
Mit der Definition
![]() bekommt man
bekommt man
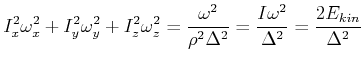 |
(6.621) |
Andererseits ist
| (6.622) |
Damit folgt die Behauptung
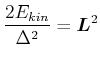 |
(6.623) |
![\includegraphics[width=0.5\textwidth]{starr-024}](img2485.gif)
Poinsot-Ellipsoid
|
Wir betrachten nun ein weiteres Ellipsoid, das Poinsot-Ellipsoid ![]() . Dieses ist ähnlich zum Trägheitsellipsoid
und liegt zu ihm konzentrisch. Wir wollen das Poinsot-Ellipsoid als Funktion von
. Dieses ist ähnlich zum Trägheitsellipsoid
und liegt zu ihm konzentrisch. Wir wollen das Poinsot-Ellipsoid als Funktion von
![]() darstellen. Die
Nutation im raumfesten Koordinatensystem wird nun beschrieben durch das Abrollen des Poinsot-Ellipsoids auf eine
Ebene
darstellen. Die
Nutation im raumfesten Koordinatensystem wird nun beschrieben durch das Abrollen des Poinsot-Ellipsoids auf eine
Ebene ![]() gegeben durch die Gesamtheit der Vektoren
gegeben durch die Gesamtheit der Vektoren
![]() . Diese Ebene
. Diese Ebene ![]() ist durch
ist durch
Am Berührungspunkt des Poinsotschen Ellipsoides muss die vorherige Gleichung auch stimmen. Deshalb ist die Ellipsengleichung im körperfesten Hauptachsensystem
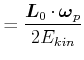 |
||
![$\displaystyle =\frac{1}{2E_{kin}}\left[ \left( I_{x}\omega_{px}\right) \omega _...
...ga_{py}\right) \omega_{py}+\left( I_{y}z\omega _{pz}\right) \omega_{pz}\right)]$](img2491.gif) |
||
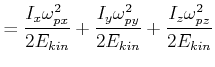 |
||
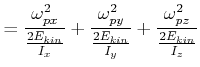 |
(6.624) |
Die drei Halbachsen des Poinsotschen Ellipsoids ![]() sind
sind
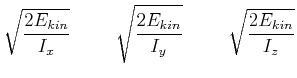
Der Punkt ![]() (Berührungspunkt zwischen dem Poinsot-Ellipsoid
(Berührungspunkt zwischen dem Poinsot-Ellipsoid ![]() und der Ebene
und der Ebene ![]() ) ist gegeben durch
) ist gegeben durch
| (6.625) |
Die Bahnkurve von ![]() auf
auf ![]() heisst Polhoide
heisst Polhoide
Die Bahnkurve von ![]() auf
auf ![]() heisst Herpolhoide
heisst Herpolhoide
Im körperfesten Hauptachsensystem ist der Winkelgeschwindigkeitsvektor
![]() die Verbindung zwischen
dem Fixpunkt 0 (beim freien Körper ist das der Schwerpunkt, beim Kreisel der Auflagepunkt) und der
Polhoide.
die Verbindung zwischen
dem Fixpunkt 0 (beim freien Körper ist das der Schwerpunkt, beim Kreisel der Auflagepunkt) und der
Polhoide.
Die Polhoide ist gegeben als Schnittpunkt des Poinsot-Ellipsoides ![]() und des Drallellipsoides
und des Drallellipsoides ![]() . Das
Drallellipsoid wird als Funktion der Variablen
. Das
Drallellipsoid wird als Funktion der Variablen
![]() ,
,![]() ,
,![]() geschrieben. Nach Gleichung (6.76) ist der Drehimpuls gegeben durch
geschrieben. Nach Gleichung (6.76) ist der Drehimpuls gegeben durch
| (6.626) |
Also können wir schreiben
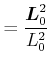 |
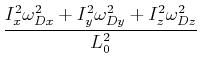 |
(6.627) | ||
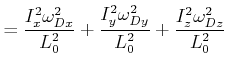 |
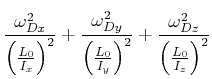 |
Diese Gleichung definiert das Drallellipsoid ![]() . Das Drallellipsoid
. Das Drallellipsoid ![]() hat die Halbachsen
hat die Halbachsen
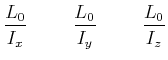
|
Bei einem reibungsfreien Kreisel ist sowohl seine kinetische Energie wie auch der Betrag seines
Drehimpulses erhalten. Die Winkelgeschwindigkeit
|
Um den Vektor
![]() vollständig anzugeben, sind drei Komponenten nötig. Mit der kinetischen Energie
vollständig anzugeben, sind drei Komponenten nötig. Mit der kinetischen Energie
![]() und dem Quadrat des Drehimpulses
und dem Quadrat des Drehimpulses
![]() haben wir erst zwei Bestimmungsgrössen. Wir könnten also
die Komponenten von
haben wir erst zwei Bestimmungsgrössen. Wir könnten also
die Komponenten von ![]() entlang einer Koordinatenachse als dritte Angabe verwenden. Üblicherweise nennt
man diese Koordinatenachse die
entlang einer Koordinatenachse als dritte Angabe verwenden. Üblicherweise nennt
man diese Koordinatenachse die ![]() -Achse: Wir bestimmen also die Komponente
-Achse: Wir bestimmen also die Komponente ![]() .
.
Dieses Tripel (![]() ,
,
![]() und
und ![]() ) ist das gleiche Tripel, das bei der Angabe der Quantenzahlen
für ein Elektron angegeben wird. Der quantenmechanische Zustand eines Elektrons in einem Atom ist also äquivalent
zu einem Bewegungszustand eines Kreisels.
) ist das gleiche Tripel, das bei der Angabe der Quantenzahlen
für ein Elektron angegeben wird. Der quantenmechanische Zustand eines Elektrons in einem Atom ist also äquivalent
zu einem Bewegungszustand eines Kreisels.
|
|
Wirkt ein externes Drehmoment
![]() bezüglich 0 so gilt
bezüglich 0 so gilt
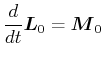 |
(6.628) |
Bemerkung: Durch den Drallsatz ist
![]() bis auf eine Konstante
bis auf eine Konstante
![]() bestimmt.
bestimmt.
|
|
|
|
Unter Präzession versteht man die Rotation von
![]() mit
mit
![]()
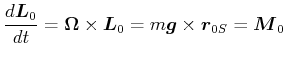 |
(6.629) |
![\includegraphics[width=0.4\textwidth]{starr-025}](img2514.gif)
Präzedierender Kreisel
|
Hier ist ![]() der Abstand des Schwerpunktes vom Fixpunkt. Dann ist
der Abstand des Schwerpunktes vom Fixpunkt. Dann ist
und daraus
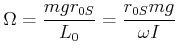 |
(6.630) |
![]() ist unabhängig von
ist unabhängig von ![]() . Wir können auch eine Energiebetrachtung machen:
. Wir können auch eine Energiebetrachtung machen:
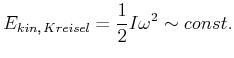 |
(6.631) |
Da ![]() konstant ist, ist auch die kinetische Energie
konstant. Die totale Energie ist konstant, also
konstant ist, ist auch die kinetische Energie
konstant. Die totale Energie ist konstant, also
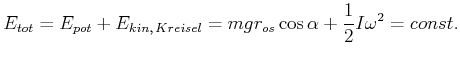 |
(6.632) |
|
|
das heisst, ![]() und
und ![]() sind auch einzeln konstant. Das heisst der präzedierende Kreisel fällt nicht.
sind auch einzeln konstant. Das heisst der präzedierende Kreisel fällt nicht.
Othmar Marti