Weiter: Kräfte und Newtonsche Gesetze Oben: Mechanik in einer Dimension Zurück: Kinematik Skript: PDF-Datei Übungen: Blätter ILIAS: Materialien Korrekturen
|
|
Wir betrachten den Stoss zweier Massen ![]() und
und ![]() auf einer reibungsarmen Luftkissenbahn. Der
Stoss soll dabei so vonstatten gehen, dass die beiden Massen nicht verändert werden. Sie sollen
also weder deformiert werden, noch soll durch den Stoss sich ihre Temperatur ändern. Wir wollen
aber keine Annahme machen über das Massenverhältnis und die Anfangsgeschwindigkeiten, sondern
mögliche Gesetze empirisch bestimmen.
auf einer reibungsarmen Luftkissenbahn. Der
Stoss soll dabei so vonstatten gehen, dass die beiden Massen nicht verändert werden. Sie sollen
also weder deformiert werden, noch soll durch den Stoss sich ihre Temperatur ändern. Wir wollen
aber keine Annahme machen über das Massenverhältnis und die Anfangsgeschwindigkeiten, sondern
mögliche Gesetze empirisch bestimmen.
![\includegraphics[width=0.99\textwidth]{mechanik-072}](img163.gif)
Situation der beiden Massen vor dem Stoss (oben) und nach
dem Stoss (unten).
|
Viele Experimente könnten die Messgrössen in Tabelle 3.1ergeben.
|
|
Wir suchen nun nach Erhaltungsgrössen, das heisst Messwerte, die alleine oder als Funktion und in Kombination summiert über beide Massen vor dem Stoss und nach dem Stoss gleich sind.
Wir haben in unserem Falle die Geschwindigkeiten ![]() und die Massen
und die Massen ![]() zur Verfügung. Ein Erhaltungssatz
könnte also wie
zur Verfügung. Ein Erhaltungssatz
könnte also wie
|
Wir finden zuerst, dass ![]() und
und ![]() zu einer Erhaltungsgrösse führt
zu einer Erhaltungsgrösse führt
| (3.16) |
Allgemein, wenn ![]() Massen involviert sind, gilt
Massen involviert sind, gilt
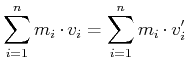 |
(3.18) |
Das heisst:
| In einem abgeschlossenen System ist der Gesamtimpuls eine Erhaltungsgrösse. |
Im Detail besprechen wir die Konsequenzen der Impulserhaltung im Abschnitt 4.4.
|
Weiter finden wir, dass für ![]() und
und ![]() die linke Seite der Gleichung
Gleichung (3.8) innerhalb der Fehlergenauigkeit gleich der rechten Seite ist. Damit
haben wir eine Erhaltungsgrösse gefunden. Die Erhaltungsgrösse ist
die linke Seite der Gleichung
Gleichung (3.8) innerhalb der Fehlergenauigkeit gleich der rechten Seite ist. Damit
haben wir eine Erhaltungsgrösse gefunden. Die Erhaltungsgrösse ist
| (3.19) |
Den Faktor
![]() begründen wir später.
begründen wir später.
Allgemein gilt
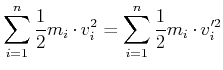 |
(3.20) |
Das heisst:
Hier ist die Gesamtenergie die kinetische Energie. Im Allgemeinen besteht die Gesamtenergie nicht nur aus der kinetischen Energie, sondern auch aus anderen Energieformen wie der potentiellen Energie, der elektrischen Energie oder der Wärme.
Für mechanische Systeme sind dies die innere Energie ![]() und die Lageenergie oder
potentielle Energie
und die Lageenergie oder
potentielle Energie ![]() . Die innere Energie ist eine Grösse, die den Energieinhalt im Teilchen
angibt. Dies kann die chemische Energie sein, aber auch die relativistische Masseenergie. Wir haben also
. Die innere Energie ist eine Grösse, die den Energieinhalt im Teilchen
angibt. Dies kann die chemische Energie sein, aber auch die relativistische Masseenergie. Wir haben also
| (3.21) |
| Energieerhaltung gilt für alle Energieformen. |
Bei inelastischen Stössen werden die beteiligten Massen verändert, sei es, dass die Massen zusammenkleben oder dass sie deformiert werden. In diesem Falle gilt die Impulserhaltung ohne jede Einschränkung. Die Energieerhaltung gilt nur, wenn die sogenannten inneren Energien berücksichtigt werden.
| Bei jedem Stoss und in jedem Teilchensystem, ob klassisch berechnet, ob relativistisch oder qunatenmechanisch berechnet gilt die Impulserhaltung. |
| Damit die Energieerhaltung gilt, muss man in der Regel neben den klassischen mechanischen Energieformen noch weitere Energieformen berücksichtigen. |
|
Stoss zweier Massen
|
Impulserhaltung (eindimensionales Problem, also kann man mit Zahlen rechnen)
Stösse heissen elastisch wenn gilt
Dann kann aus Gleichung (3.15) und Gleichung (3.16) ![]() und
und ![]() ausgerechnet werden.
ausgerechnet werden.
Wir schreiben die Gleichungen um und erhalten
| (3.24) |
und
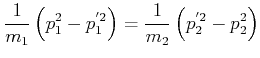 |
Ausmultipliziert bekommen wir
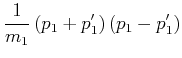 |
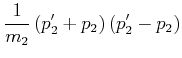 |
(3.25) | |
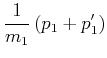 |
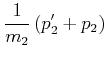 |
(3.26) |
| (3.27) |
Also ist die Relativgeschwindigkeit nach dem Stoss (
![]() ) das Negative der Relativgeschwindigkeit vor
dem Stoss (
) das Negative der Relativgeschwindigkeit vor
dem Stoss (
![]() ).
).
Das bedeutet, dass bei einer Frontalkollision von einem Auto (
![]() ) mit einem Fussgänger
(
) mit einem Fussgänger
(
![]() ) die Relativgeschwindigkeit vorher (
) die Relativgeschwindigkeit vorher (
![]() ) gleich dem negativen der
Relativgeschwindigkeit nach dem Stoss ist. Da das Auto aber (siehe unten) nur unwesentlich abgebremst wird, fliegt
der Fussgänger nach dem Stoss mit
) gleich dem negativen der
Relativgeschwindigkeit nach dem Stoss ist. Da das Auto aber (siehe unten) nur unwesentlich abgebremst wird, fliegt
der Fussgänger nach dem Stoss mit
![]() durch die Gegend.
durch die Gegend.
Die Impulse nach dem Stoss sind dann
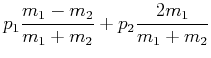 |
(3.28) | ||
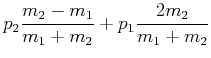 |
(3.29) |
Es gibt die folgenden Spezialfälle:
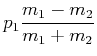 |
(3.30) | ||
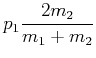 |
(3.31) |
| (3.32) | |||
| (3.33) |
| (3.34) | |||
| (3.35) |
Wir nennen einen Stoss vollkommen plastisch, wenn die beiden Körper nach dem Stoss aneinander kleben, wenn sie
quasi zu einer Masse (
![]() ) mit einer Geschwindigkeit (
) mit einer Geschwindigkeit (
![]() ) geworden
sind. Dann ist
) geworden
sind. Dann ist
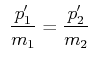 |
(3.36) |
Die Impulserhaltung ergibt dann
| (3.37) | |||
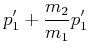 |
(3.38) | ||
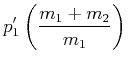 |
(3.39) | ||
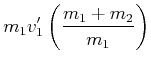 |
(3.40) | ||
| (3.41) | |||
| (3.42) |
und damit für die Teilimpulse
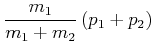 |
(3.43) | ||
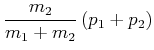 |
(3.44) |
Beim plastischen Stoss ist die Energie nicht erhalten. Wir bezeichnen mit ![]() die Energie, die in Wärme und
Deformation gespeichert wird.
die Energie, die in Wärme und
Deformation gespeichert wird.
| (3.45) | |||
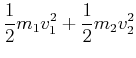 |
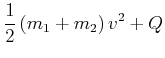 |
(3.46) |
Für die Endgeschwindigkeit hatten wir
![]() und damit
und damit
![]() . Eingesetzt
. Eingesetzt
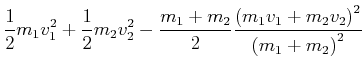 |
(3.47) | ||
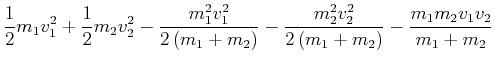 |
(3.48) | ||
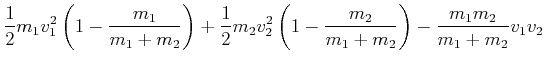 |
(3.49) | ||
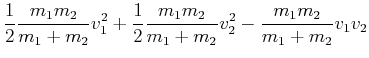 |
(3.50) | ||
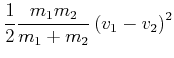 |
(3.51) |
Die Grösse
![]() heisst auch die reduzierte Masse. Mit
ihr können Zweikörper-Probleme im Schwerpunktssystem einfacher gelöst werden.
heisst auch die reduzierte Masse. Mit
ihr können Zweikörper-Probleme im Schwerpunktssystem einfacher gelöst werden.
Othmar Marti