 | Versuch zur Vorlesung: |
| Auflösungsvermögen eines Mikroskops (Versuchskarte O-001) | |
Wir verwenden die Tatsache, dass optische Systeme in den einfachsten Fällen lineare Systeme sind. Wenn f(x,y) und g(x,y) Intensitätsverteilungen senkrecht zur optischen Achse sind, und f die Ausgangsverteilung und g die Bildverteilung ist, schreibt man für die Abbildung
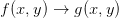 | (5.1) |
Die Abbildung ist linear, das heisst, wenn f1 → g1 und f2 → g2 ist, ist
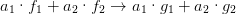 | (5.2) |
Wir nennen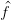 
(u,v) die Fouriertransformation von f(x,y).
Es gilt
![∫
f(x,y ) = f^(u, v)e2πi[ux+vy]dudv
∫
^f(u,v ) = f (x, y)e-2πi[ux+vy]dxdy (5.3)](op-2015-2016796x.png)
Wir schreiben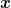 
= (x,y) und 
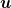= (u,v) Die
Fouriertransformation lässt sich dann kompakt schreiben
als
![∫ ^ 2πi[u· ]
f (x) = f(u )e du
∫ - 2πi[u·x]
f^(u) = f(x )e dx (5.4)](op-2015-2016799x.png)
 | Versuch zur Vorlesung: |
| Fourier-Transformation (Versuchskarte O-067) | |
Ein Lichtfleck an der Position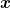 
′ der Eingangsebene erzeugt
eine Intensitätsverteilung in der Ausgangsebene, die sowohl
vom Beobachtungspunkt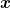 
wie auch von 
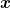′ abhängt. Die
Impulsantwort ist
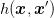 | (5.5) |
Ein optisches System ist translationsinvariant, wenn
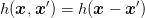 | (5.6) |
gilt. Bei einem kontinuierlichen linearen optischen System gilt zwischen der Bildebene und der Eingangsebene die Beziehung
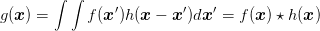 | (5.7) |
Dies ist das Faltungstheorem aus der Fourieroptik. Im Fourierraum wird aus einer Faltung eine Multiplikation, also
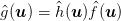 | (5.8) |
Wenn die optische Übertragung kohärent verläuft, dann verwendet man die oben definierte kohärente Übertragungsfunktion, die Amplituden verknüpft. Ist die Übertragung nicht kohärent, muss man mit Intensitäten rechnen.
__________________________________________________________________________
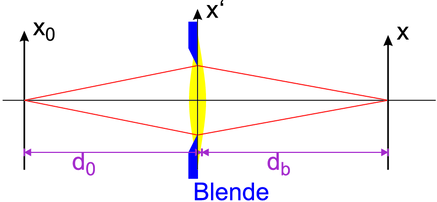
Berechnung der Beugung an einer Öffnung
_____________________________________________________________________
Das entstehende Beugungsbild eines Punktes ist das Fraunhofersche Beugungsmuster der Blendenöffnung. Die inkohärente Impulsantwort wird
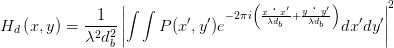 | (5.9) |
Dies bedeutet, dass Hd das Betragsquadrat der Fouriertransformation der Pupillenfunktion P ist.
Für eine kreisförmige Öffnung ist die Pupillenfunktion
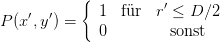 | (5.10) |
wobei D den Durchmesser der Öffnung und r′ =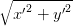 
den Radius darstellt.
Die Rechnung ist in Polarkoordinaten einfacher.
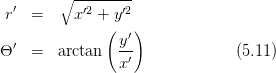
sowie in der Bildebene
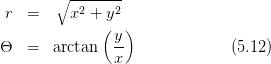
Mit ρb = r∕(λdb) bekommt man
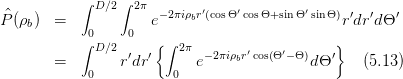
Dabei ist die Grösse
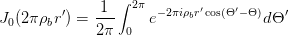 | (5.14) |
die sogenannte Besselfunktion nullter Ordnung. Die Fouriertransformation einer runden Pupille wird also
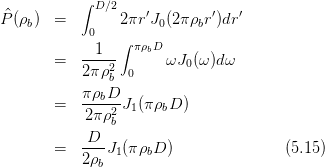
J1(α) = ∫ 0αωJ 0(ω)dω ist die Besselfunktion erster Ordnung. Mit r = λdbρb, Θ und S = πD2∕4, der Pupillenfläche, bekommt man für die komplexe Amplitude
![[ ]
^ 2J1-(πρbD-)
ψ(r) = P(ρb) = S πρbD
[ ]2
2 2 2J1-(πρbD-)
I(r) = |ψ (r)| = S πρbD (5.16)](op-2015-2016815x.png)
Die Intensitäten als Funktion von X = ρbD sind
| X | 0 | 1.22 | 1.63 | 2.33 | 2.68 | 3.33 |
![[2J1(πX )∕ (πX )]](op-2015-2016816x.png) 2 | 1 | 0 | 0.017 | 0 | 0.004 | 0 |
_______________________________________________
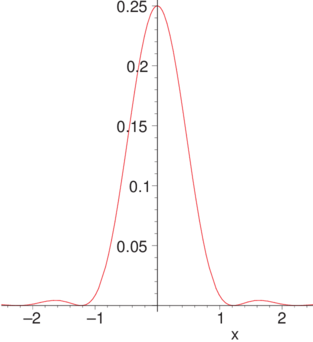
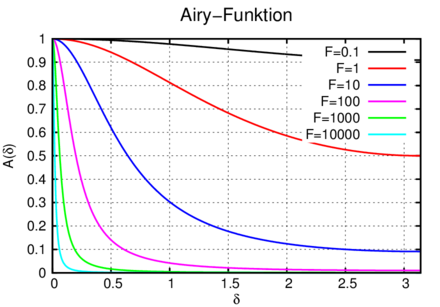
Die Beugung an einer ringförmigen Apertur.
_____________________________________________________________________
Bei der Beugungsfigur an einer kreisförmigen Öffnung mit
dem Durchmesser d ist das erste Minimum bei sin Θ = 1.22
.
__________________________________________________________________________
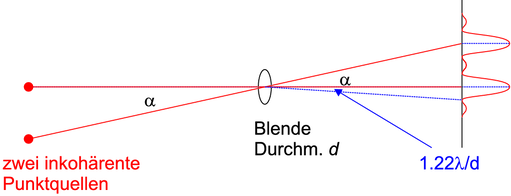
Abbildung zweier punktförmiger, inkohärenter Quellen durch eine Blende mit der Öffnung d.
_____________________________________________________________________
Bei dem sogenannten kritischen Winkel αK, der durch
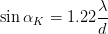 | (5.17) |
gegeben ist, fällt das Minimum der einen Beugungsfigur gerade auf das Maximum der anderen. Das obige Kriterium wird das Rayleighsche Auflösungskriterium genannt.
__________________________________________________________________________
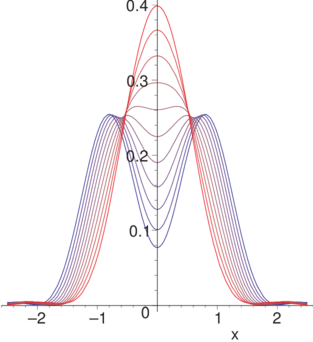
Form der Intensität bei der Überlagerung zweier inkohärenter Punktquellen. Der Abstand variiert von 0.6 (rot) bis 1.6 (blau) in Schritten von 0.1.
_____________________________________________________________________
Diese Abbildung zeigt, dass die Definition des Auflösungsvermögens an das mögliche Signal-Rausch-Verhältnis gebunden ist. Mit modernen Detektoren mit 16 Bit Auflösung sind deshalb leicht bessere Grenzen der Auflösung möglich.
__________________________________________________________________________
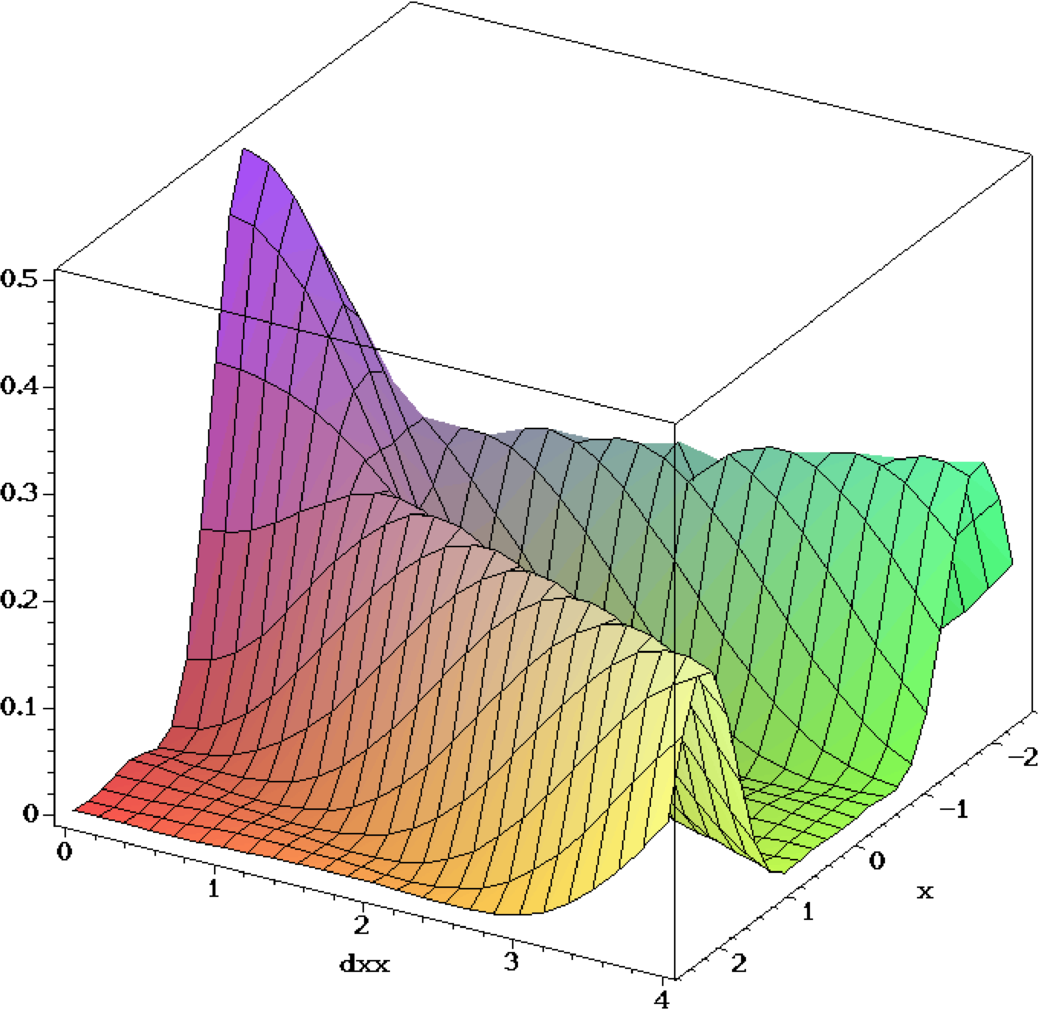
Querschnitt zweier inkohärenter Punktquellen als Funktion des Abstandes (links) und Bild der Intensitätsverteilung bei einem Abstand von 1.
_____________________________________________________________________
Wenn das zu untersuchende Objekt in ein Medium mit dem
Brechungsindex n eingebettet ist, dann verbessert sich die
Auflösung auf sin αK = 1.22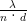
, da in diesem Medium die
Wellenlänge ja λ′ = λ∕n ist.
Lizenzinformationen