__________________________________________________________________________
Prinzip einer Faltung
_____________________________________________________________________

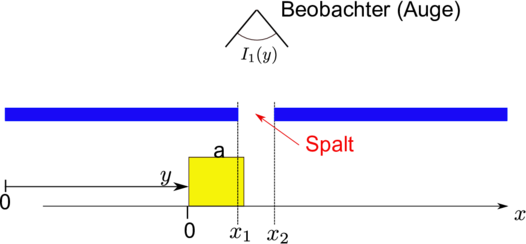
Die im Abschnitt 3.3.3 vorgestellte Fouriertransformation ist eine lineare Transformation (siehe z.B. [AW95, BSMM08]). Hier soll die Faltung diskutiert werden. Dazu überlegen wir, wie hoch die Gesamtenergie von Licht ist, das von einer begrenzten Leuchte mit konstanter Intensität durch einen Spalt geschickt wird, wobei die Leuchte am Spalt vorbei bewegt wird.
__________________________________________________________________________

Prinzip einer Faltung
_____________________________________________________________________
Abbildung 3.10.1 zeigt das Prinzip einer Faltung. Wenn die Leuchte ganz vom Spalt abgedeckt wird, ist die Intensität I1 = 0. Wenn die Leuchte teilweise vom Spalt abgedeckt wird, hängt die Intensität I1 von der Position ab. Ist die Leuchte im Spalt, ist die Intensität I1 wieder konstant.
__________________________________________________________________________
Faltung einer Rechteckfunktion an einem Spalt
_____________________________________________________________________
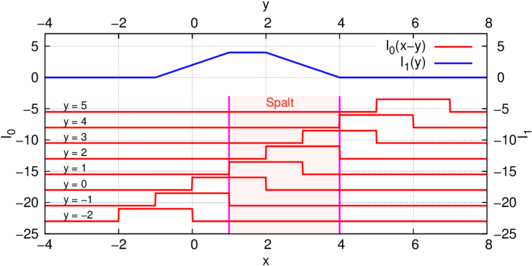
Abbildung 3.10.1 zeigt ein gerechnetes Beispiel. Die rote rechteckförmige Kurve I0 wird am Spalt vorbeigeschoben. Die blaue Kurve I1 zeigt das Resultat. Formal wird eine Faltung in einer Dimension durch die Integralgleichung
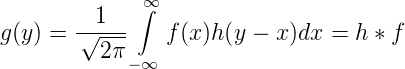 | (3.1) |
beschrieben (Siehe [AW95, p865]). ∗ ist das Operationszeichen für eine Faltung. Hecht [Hec05, p 859] schreibt
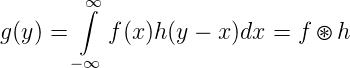 | (3.2) |
Der Unterschied rührt wieder von der Verteilung des Faktors 1∕(2π) her. Beachten Sie auch, dass bei Hecht ⊛ das Operatorzeichen für eine Faltung ist.
Faltungen können besonders effizient über die Fouriertransformation berechnet werden:
| Die Fouriertransformation einer Faltung zweier Funktionen ist das Produkt der Fouriertransformationen der beiden Funktionen. |
Die Diracsche Deltafunktion nach Gleichung (B.3) hat eine besonders einfache Fouriertransformation
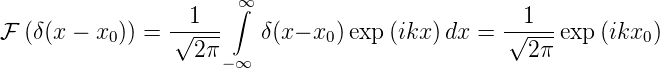 | (3.4) |
Das Resultat ist also eine Funktion mit konstanter komplexer Amplitude. Umgekehrt ist die Fouriertransformation einer konstanten Funktion eine Dirac-Delta-Funktion
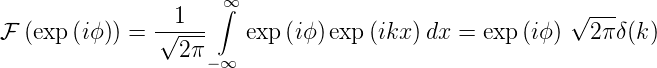 | (3.5) |
Die Interpretation dieser Gleichungen zum Beispiel für Schall ist: ein extrem kurzer Knall enthält alle Schallfrequenzen.
| Literatur | |
| Versuch zur Vorlesung: | |
| Beugung am Doppelspalt (Versuchskarte O-123) | |
Perfekte Spalte, also Spalte mit verschwindender Breite können über Dirac-Deltafunktionen (B.3) modelliert werden. Ein Beugungsobjekt mit mehreren gleichabständigen identischen Spalten kann als Faltung
Dies kann auch so formuliert werden:
| Bei Doppelspalten oder bei Gittern mit N Linien setzt sich das Beugungsmuster aus dem Muster des Einzelspaltes multipliziert mit dem Beugungsmuster des Gitters zusammen. |
Da die charakteristische Länge des Einzelspaltes kleiner ist als die Gitterperiode, ist das Beugungsmuster des Einzelspaltes breiter als das des Gitters. Die Beugungsfunktion des Einzelspaltes gibt die Umhüllende des Beugungsmusters.
Wir hatten für das Beugungsmuster des Doppelspalts mit linienförmigen Spalten
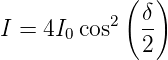 | (3.6) |
wenn wir n = 1 setzen. Das gesamte Beugungsmuster ist dann durch
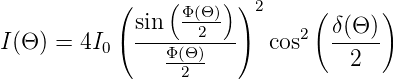 | (3.7) |
wobei Φ(Θ) = 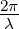 a sin Θ und δ(Θ) =
a sin Θ und δ(Θ) = 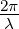 d sin Θ sind mit a
der Spaltbreite und d dem Abstand der beiden Spalte. Wir
können nun noch mit Θ(y) = arctan
d sin Θ sind mit a
der Spaltbreite und d dem Abstand der beiden Spalte. Wir
können nun noch mit Θ(y) = arctan 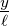 das Beugungsmuster
für einen ebenen Schirm berechnen.
das Beugungsmuster
für einen ebenen Schirm berechnen.
__________________________________________________________________________
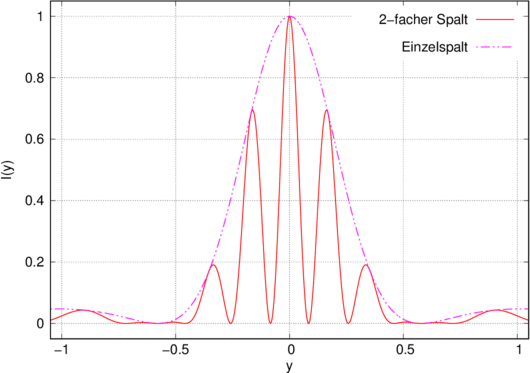
Beugung an einem Doppelspalt mit dem Spaltabstand d = 6 und der Spaltbreite a = 2.
_____________________________________________________________________
_____________________________________________________________________
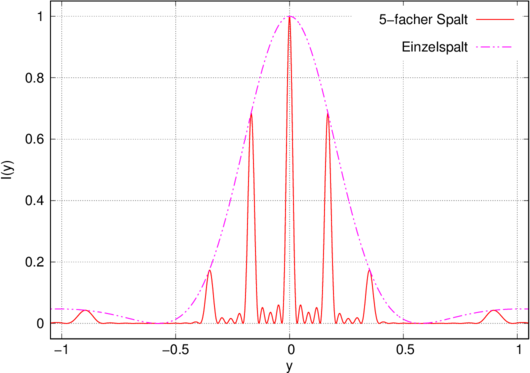
Beugung an einem 5-fach Spalt mit dem Spaltabstand d = 6 und der Spaltbreite a = 2
__________________________________________________________________________
 Lizenzinformationen
Lizenzinformationen