![Ψ (x, t) = Ψ0(x )exp [iu(x, t)] = Ψ0 (x)exp [i(k(x )·x − ωt)]](op-2016-2017287x.png)

| Literatur | |
| Versuch zur Vorlesung: | |
| Wellenwanne (Versuchskarte O-021) | |
Die Wellenfunktion für eine zeitunabhängige Welle in zwei oder drei Dimensionen wird wie
![Ψ (x, t) = Ψ0(x )exp [iu(x, t)] = Ψ0 (x)exp [i(k(x )·x − ωt)]](op-2016-2017287x.png) | (3.1) |
für eine longitudinale Welle und
![A (x,t) = A0(x )exp [iu (x, t)] = A0 (x)exp [i(k(x )·x − ωt)]](op-2016-2017288x.png) | (3.2) |
für transversale Wellen. 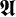 (
(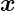 ) ist ein Vektor, der auch
komplexe Komponenten haben kann (Die komplexen
Komponenten geben die Phasen an.). Der Vektor, der aus
dem Betrag der einzelnen Komponenten gebildet wird, gibt
die Schwingungsrichtung der Welle an. Für eine transversale
Welle gilt
) ist ein Vektor, der auch
komplexe Komponenten haben kann (Die komplexen
Komponenten geben die Phasen an.). Der Vektor, der aus
dem Betrag der einzelnen Komponenten gebildet wird, gibt
die Schwingungsrichtung der Welle an. Für eine transversale
Welle gilt
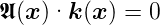 | (3.3) |
__________________________________________________________________________
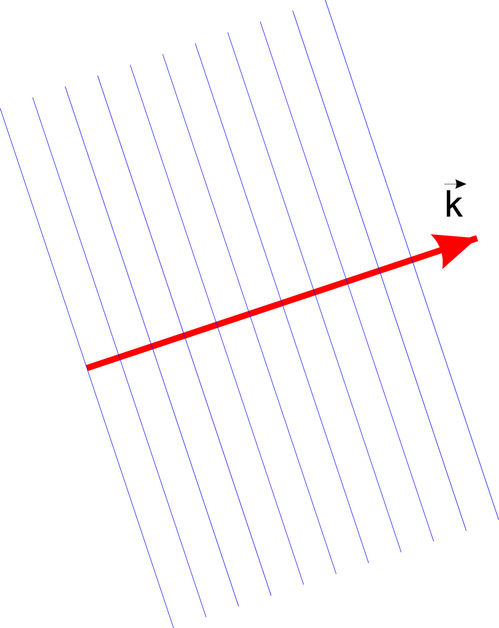
Bild einer ebenen Welle
_____________________________________________________________________
Eine ebene Welle entsteht aus der allgemeinen Lösung der
Wellengleichung dadurch, dass die Amplitude und der
Wellenvektor 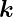 nicht vom Ort abhängen. Eine ebene
Transversalwelle ist durch
nicht vom Ort abhängen. Eine ebene
Transversalwelle ist durch
![A (x,t) = A0 exp [i(k·x − ωt)],](op-2016-2017293x.png) | (3.4) |
eine Longitudinalwelle durch
![Ψ (x,t) = Ψ0 exp [i (k ·x − ωt)].](op-2016-2017294x.png) | (3.5) |
gegeben.
Die Ausbreitungsrichtung ebener Wellen ist durch den
Wellenvektor 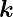 gegeben. Eine Vektor gezeichnet parallel zu
gegeben. Eine Vektor gezeichnet parallel zu 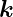 kann so die Ausbreitungsrichtung anzeigen. Bei ebenen
Lichtwellen spricht man dann von Lichtstrahlen.
kann so die Ausbreitungsrichtung anzeigen. Bei ebenen
Lichtwellen spricht man dann von Lichtstrahlen.
| Achtung! Mathematisch streng muss eine ebene Welle eine unendliche Ausdehnung haben. Sie beginnt und endet nur im Unendlichen. Alle „ebenen Wellen“ und alle „Lichtstrahlen“ sind nur mehr oder weniger gute Approximationen der physikalisch nicht realisierbaren Mathematik. |
| Literatur | |
| Versuch zur Vorlesung: | |
| Wellenwanne (Versuchskarte O-021) | |
Eine weitere häufig vorkommende Form von Wellen sind die Kugelwellen. Auch sie sind eine Lösung der aus den Maxwellgleichungen abgeleiteten Wellengleichung (2.1), aber in Kugelkoordinaten. Wir verwenden den Laplace-Operator in Kugelkoordinaten aus Gleichung (B.12)
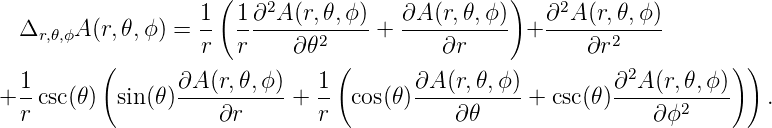 |
Wir interessieren uns hier zuerst nur für kugelsymmetrische Lösungen, also Lösungen, die nicht von 𝜃 und ϕ abhängen. Alle Ableitungen nach 𝜃 und ϕ sind dann null. Der Laplace-Operator hat für kugelsymmmetrische Probleme die Form
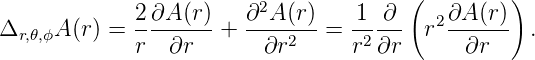 | (3.6) |
Damit ist die Wellengleichung
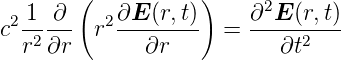 | (3.7) |
Gleichung (3.7) ist in Wirklichkeit drei Gleichungen. Diese Gleichungen können durch einen Separationsansatz gelöst werden (siehe z.B. Bücher zur Atomphysik). Wir nehmen eine Koordinate und raten, dass die Amplitude
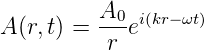 | (3.8) |
eine Lösung ist. Eingesetzt erhalten wir
Wenn die Bedingung in Gleichung (3.9f) erfüllt ist, ist Gleichung (3.8) eine Lösung eine Lösung der Wellengleichung (3.7) in Kugelkoordinaten für kugelsymmetrische Probleme. Für eine auslaufende Welle ist c = ω∕k, für eine einlaufende Welle ist c = −ω∕k.
Alternativ hätten wir die Amplitudenabhängigkeit durch folgende Überlegung erhalten können:
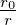 sein.
sein.
__________________________________________________________________________
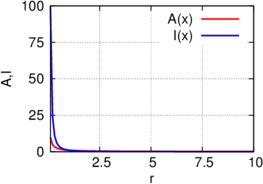
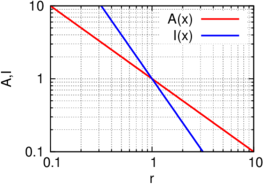
Amplitude und Intensität einer Kugelwelle in Abhängigkeit der Distanz r von der Quelle. Links eine lineare, rechts eine logarithmische Darstellung.
_____________________________________________________________________
| Bei einer Kugelwelle ist
|
| Versuch zur Vorlesung: | |
| Moire-Modell der Interferenz von Kugelwellen (Versuchskarte O-019) | |
Eine beliebige in der Zeit periodische Funktion f(t) (mit der Periode T = 2π∕ω), die genügend oft stetig differenzierbar ist, kann durch Sinus- und Cosinusfunktionen dargestellt werden [AW95, p 808ff].
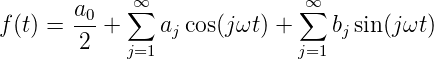 | (3.10) |
Wir können aj und bj wie folgt ausdrücken [AW95, p 808ff]:
Mit komplexen Funktionen und komplexen Koeffizienten lauten die Gleichungen (3.10)
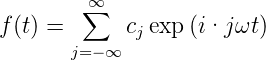 | (3.12) |
und (3.11)
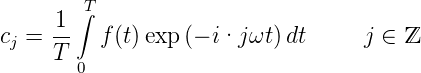 | (3.13) |
Auf dem Einheitskreis z = exp(i𝜃) entspricht dies der Entwicklung von
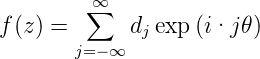 | (3.14) |
in eine Laurent-Reihe [AW95, p 809].
Eine Erweiterung der Laurent-Reihen ist die Fourier-Transformation für beliebige genügend oft stetig differenzierbare komplexwertige Funktionen eines komplexen Arguments [AW95, p 846ff]:
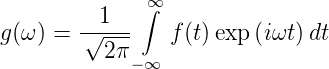 | (3.15) |
sowie die Rücktransformation
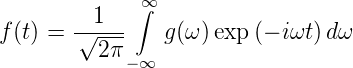 | (3.16) |
Die Literatur ist nicht eindeutig, wie der Faktor (2π)−1 verteilt wird. So schreibt zum Beispiel [Hec05, p 839] für die Transformation
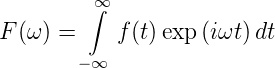 | (3.17) |
sowie für die Rücktransformation
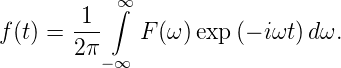 | (3.18) |
Hecht hat dabei noch die Konvention verwendet, dass grosse Buchstaben die Fouriertransformierte beschreiben.
Anstelle der Integrale wird oft auch F für die Transformation und F−1 für die Rücktransformation verwendet, also in der Hechtschen Notation
 | (3.19) |
Würden wir in Gleichung (3.15) t durch t = a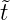 ersetzen,
hätten wir also auch dt = ad
ersetzen,
hätten wir also auch dt = ad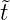 und
und
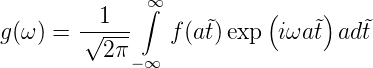 | (3.20) |
Nun sieht natürlich Gleichung (3.20) nicht mehr wie die
Definition der Fouriertransformation aus. Wir können dies
beheben, indem wir nun mit 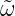 = aω rechnen und den
zusätzlichen Faktor a weglassen. Dann haben wir
= aω rechnen und den
zusätzlichen Faktor a weglassen. Dann haben wir
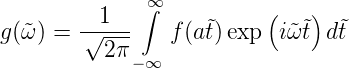 | (3.21) |
In der Hechtschen Notation folgt jetzt aus G(ω) = F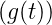 dass für eine gestreckte Achse t∕a die Fouriertransformation
dass für eine gestreckte Achse t∕a die Fouriertransformation
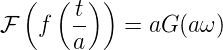 | (3.22) |
ist.
In 2 Dimensionen, wichtig für die Optik lauten die
Gleichungen mit 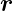 = (x,y)T und
= (x,y)T und 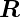 = (u,v)T
= (u,v)T
Dabei wurden zwei Konventionen verwendet:
In drei Dimensionen lauten die Fourier-Transformationen
mit 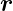 = (x,y,z)T und
= (x,y,z)T und 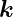 = (k
x,ky,kz)T :
= (k
x,ky,kz)T :
 Lizenzinformationen
Lizenzinformationen