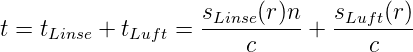

| Literatur | |
Als Vorstufe betrachten wir die durch eine Linse induzierte abstandsabhängige Phasendifferenz für paraxiale Strahlen. Die Linsenkrümmung sei R. Die x,y-Ebene sei senkrecht zur optischen Achse. Dann ist die Dicke der Sammellinse durch d(x,y) = d0 − (x2 + y2)∕2R 1 − (x2 + y2)∕2R 2 gegeben. Der optische Weg setzt sich dann aus s = sLinse(r) + sLuft(r) zusammen. Die Zeit, die Das Licht für das durchlaufen dieser Strecke benötigt ist
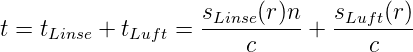 | (7.1) |
Mit sLuft = s0 −sLinse und unter Weglassung aller konstanten Terme bekommt man
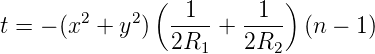 | (7.2) |
Mit 1∕f = (n − 1)(1∕R1 + 1∕R2) ist das Resultat
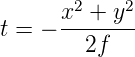 | (7.3) |
Wenn wir mit EL(x,y) die Amplitudenverteilung links von der Linse und mit ER(x,y) die Verteilung rechts von der Linse beschreiben, gilt
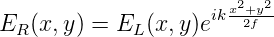 | (7.4) |
Den gleichen Effekt erreicht man mit einem Medium, das die folgende Variation des Brechungsindexes hat
![[ ]
k2 2 2
n(x,y ) = n0 1 − 2k-(x + y )](op-2016-2017881x.png) | (7.5) |
Das Resultat aus Abschnitt 7.1.6 lautet
Aus der Elektrizitätslehre folgt (ohne Ableitung), dass für das elektrische Feld
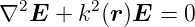 | (7.7) |
gilt. Wir beschränken uns auf den Fall wo k2(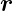 ) = k2 −kk
2r2
gilt. Der Laplace-Operator in Zylinderkoordinaten für
Funktionen, die nur von r =
) = k2 −kk
2r2
gilt. Der Laplace-Operator in Zylinderkoordinaten für
Funktionen, die nur von r = 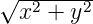 abhängen, ist
abhängen, ist
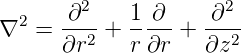 | (7.8) |
Wir verwenden die Abkürzung ∇t2 = 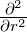 +
+ 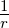
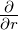 . Weiter
setzen wir an:
. Weiter
setzen wir an:
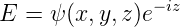 | (7.9) |
und erhalten
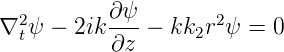 | (7.10) |
Wenn die Intensität entlang z sich nur wenig ändert (k(∂ψ∕∂z) » ∂2ψ∕∂z2 « k2ψ, ist, können wir für ψ ansetzen
![{ [ ]}
1- 2
ψ (x,y,z) = exp − i P (z) + 2Q (z)r](op-2016-2017892x.png) | (7.11) |
Wir setzen dies ein und bekommen
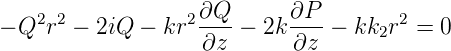 | (7.12) |
Da dies Gleichung für alle r gelten soll, müssen die Koeffizienten der verschiedenen Potenzen von r einzeln verschwinden. Also ist
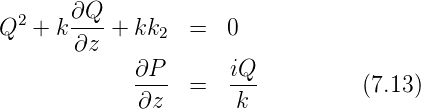
In einem homogenen Medium ist k2 = 0 so dass wir die Gleichung
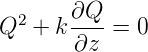 | (7.14) |
erhalten. Wir definieren die Funktion s(z) über
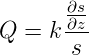 | (7.15) |
Durch Einsetzen sehen wir, dass
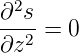 | (7.16) |
Damit muss s(z) = az + b sein. Somit ist Q
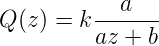 | (7.17) |
Bequemer ist es im weiteren, wenn wir die Funktion
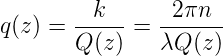 | (7.18) |
verwenden. Diese hat die Form
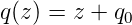 | (7.19) |
Wir setzen Q(z) in die Gleichung für P(z) ein und erhalten
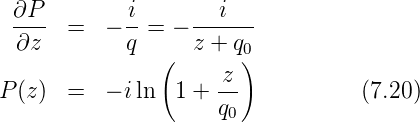
Wir nehmen an, dass q0 rein imaginär ist. Dann gilt für die örtliche Amplitudenverteilung
![{ [ ( ) ]}
ψ (r,z ) = exp − i − iln 1 + z- + ----k----r2
q0 2(q0 + z)](op-2016-2017902x.png) | (7.21) |
Wir setzen q0 := i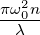 , berücksichtigen λ = 2πn∕k und
verwenden die Identität ln(a + ib) = ln
, berücksichtigen λ = 2πn∕k und
verwenden die Identität ln(a + ib) = ln 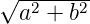 + i arctan(b∕a)
und erhalten für den ersten Term im obigen Produkt
+ i arctan(b∕a)
und erhalten für den ersten Term im obigen Produkt
![[ ( )] [ ( ) ]
exp − ln 1 − i-λz--- = ∘----1------exp iarctan -λz--
πω20n 1 + -λ2z2- πω0n
π2ω40n2](op-2016-2017905x.png) | (7.22) |
Der zweite Term wird
![( )
[ 2 ] ||{ 2 2 ||}
exp -−-ikr--- = exp ---[--−(r----)-]-− ---[--ikr(----)-]
2(q0 + z) ||( ω2 1 + -λz2- 2 2z 1 + πω0n 2 ||)
0 πω0n λz](op-2016-2017906x.png) | (7.23) |
Die folgenden Definitionen sind üblich
![⌊ ⌋
( λz )2 ( z2 )
ω2 (z) = ω20⌈1 + ---2-- ⌉ = ω20 1 + -2- (7.24)
πω 0n z0
[ ( )2] ( 2)
R (z) = 1 + πω0n- = z 1 + z0- (7.25)
λz z2
( λz ) ( z )
η(z) = arctan --2--- = arctan -- (7.26)
πω0n z0
πω20n
z0 ≡ ------ (7.27)
λ](op-2016-2017907x.png)
Die Parameter haben die folgende Bedeutung:
| ω(z) | Der halbe Strahldurchmesser an der Position z |
| R(z) | Der Krümmungsradius der Wellenfront an der Stelle z |
| η(z) | Phasenfaktor |
| z0 | Ort der maximalen Krümmung der Wellenfront |
Mit dieser abgekürzten Schreibweise wird
![[ ( ) ]
E (x,y,z) = E -ω0--exp − i (kz − η(z)) − r2 ---1--+ -ik---
0ω(z) ω2 (z) 2r(z)](op-2016-2017908x.png) | (7.28) |
Weiter ist
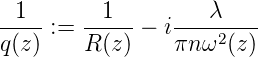 | (7.29) |
Die Grösse 1∕q(z) beschreibt die Gaussschen Strahlen. Der Realteil gibt den Krümmungsradius der Wellenfronten, der Imaginärteil den Strahldurchmesser.
| Die Grösse q(z) ist deshalb sehr wichtig, weil mit Hilfe der Transfermatrizen q(z) propagiert werden kann. Die Transfermatrizen geben deshalb auch die Änderung der Strahlform durch optische Elemente an. |
| Literatur | |
Die obigen Parameter haben die folgende Bedeutung
Die transversale Amplitudenverteilung folgt einer Gausskurve, wie man aus dem Term exp[r2∕ω2(z)] ersehen kann. ω(z) ist die Distanz zur optischen Achse, bei der die Intensität um den Faktor e vom Maximum abgefallen ist. ω0 beschreibt den minimalen Strahldurchmesser.
R(z) ist der Krümmungsradius der Wellenfronten. Aus
R(z) = z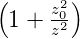 ist ersichtlich, dass lim z→0R(z) = ∞ ist.
Damit nähern Gausssche Wellen im Fokus eine ebene Welle
an. Ebenso ist lim z→±∞R(z) = ±∞. Auch für sehr grosse
Distanzen sind Gausssche wellen eine gute Approximation für
ebene Wellen.
ist ersichtlich, dass lim z→0R(z) = ∞ ist.
Damit nähern Gausssche Wellen im Fokus eine ebene Welle
an. Ebenso ist lim z→±∞R(z) = ±∞. Auch für sehr grosse
Distanzen sind Gausssche wellen eine gute Approximation für
ebene Wellen.
Weit weg vom minimalen Strahldurchmesser kann ein Gaussscher Strahl durch einen Öffnungswinkel
 | (7.30) |
beschrieben werden. Es gilt deshalb die folgende Gleichung
 | (7.31) |
die formal äquivalent zur Unschärferelation ist. Damit ist
klar, dass ein kleinerer Brennfleck unweigerlich einen grösseren
Öffnungswinkel bedeutet. In einer nullten Approximation sieht
man auch, dass ω0 ≥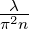 sein muss.
sein muss.
Die Transformation eines Gaussschen Strahls mit optischen Elementen, die durch die Matrix
![[ ]
A B
C D](op-2016-2017914x.png) |
charakterisiert sind, wird durch
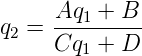 | (7.32) |
beschrieben. Zum Beispiel wirkt eine Linse mit der Brennweite −f, also der Matrix
![[ ]
1 0
− 1∕f 1](op-2016-2017916x.png) |
so auf einen Gaussschen Strahl
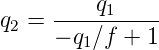 | (7.33) |
Wir nehmen den Kehrwert und bekommen
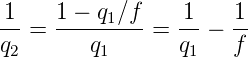 | (7.34) |
Mit der Definition 1∕q = 1∕R + iλ∕(πnω2) wird die Gleichung
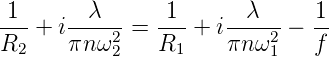 | (7.35) |
Diese Gleichung muss für den Real- und den Imaginärteil separat erfüllt sein. Also haben wir
Wenn zwei optische Elemente mit den Matrizen
![[ ]
A1 B1
C1 D1](op-2016-2017921x.png) |
und
![[ ]
A2 B2
C2 D2](op-2016-2017922x.png) |
hintereinander geschaltet, ist das Resultat durch
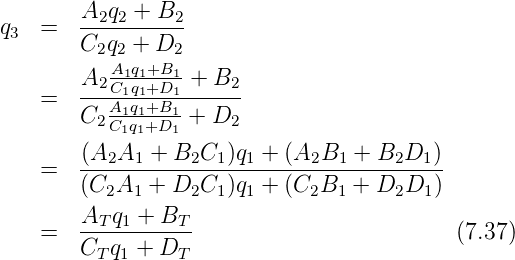
gegeben. Die Analyse dieser Gleichung zeigt, dass für die Koeffizienten auch
![[ A B ] [ A B ] [ A B ]
T T = 2 2 1 1
CT DT C2 D2 C1 D1](op-2016-2017924x.png) | (7.38) |
gilt. Damit gelten für Gausssche Strahlen die gleichen mathematischen Formeln für die Berechnung von optischen Systemen wie bei Lichtstrahlen.
__________________________________________________________________________
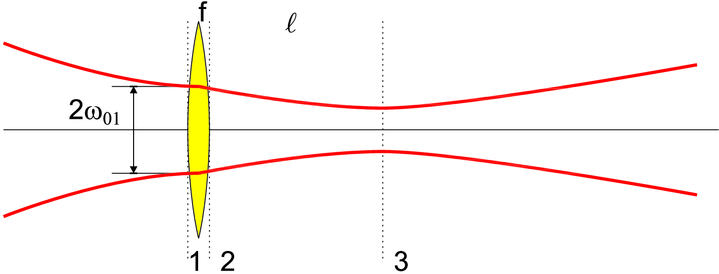
Fokussierung eines Gaussschen Strahls.
_____________________________________________________________________
In der Eingangsebene 1 ist R1 = ∞ und ω = ω01. Dann ist
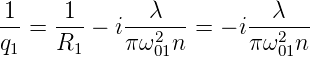 | (7.39) |
In der Ebene 2 ist
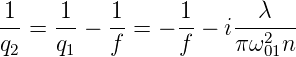 | (7.40) |
Damit ist
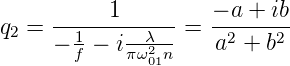 | (7.41) |
wobei a = 1∕f und b = λ∕(πω012n). In der Ebene 3 ist
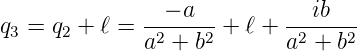 | (7.42) |
Nun muss in der Ebene 3 auch gelten
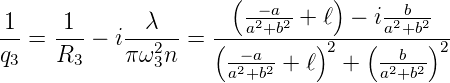 | (7.43) |
In der Ebene 3 soll der Durchmesser minimal sein, also ist R3 = ∞. Damit muss in der obigen Gleichung der Realteil null sein. Damit ergibt sich die Bedingung
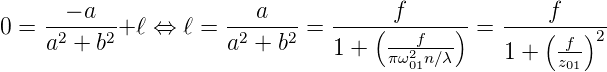 | (7.44) |
Und damit ist auch der Ort des Strahlminimums gegeben. Der neue Strahldurchmesser ist
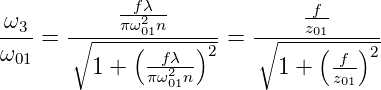 | (7.45) |
Der Parameter z0 ist der konfokale Parameter, der angibt, in
welcher Distanz vom Strahlminimum der Strahldurchmesser
um 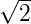 zunimmt. Der Wert des konfokalen Parameters
ist
zunimmt. Der Wert des konfokalen Parameters
ist
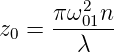 | (7.46) |
| Literatur | |
| Versuch zur Vorlesung: | |
| Laser (Versuchskarte AT-052) | |
Die Gaussschen Strahlen sind die Grundmode von Laserstrahlung. Sie zeichnen sich dadurch aus, dass sie keine Knotenlinie hat. Es existieren weiter Moden, die durch die Anzahl Knotenlinien in horizontaler und vertikaler Richtung charakterisiert sind. Die möglichen Moden sind durch die Randbedingungen vorgegeben. So erzeugt eine vertikale Störung durch die Resonatorachse eine Mode mit zwei Maxima, die durch eine vertikale Knotenlinie getrennt sind.
Im folgenden werden Messungen von Moden gezeigt, die im Institut für Experimentelle Physik an vertikal emittierenden Laserdioden (VCSEL) aus der Abteilung Optoelektronik gemessen wurden.
__________________________________________________________________________
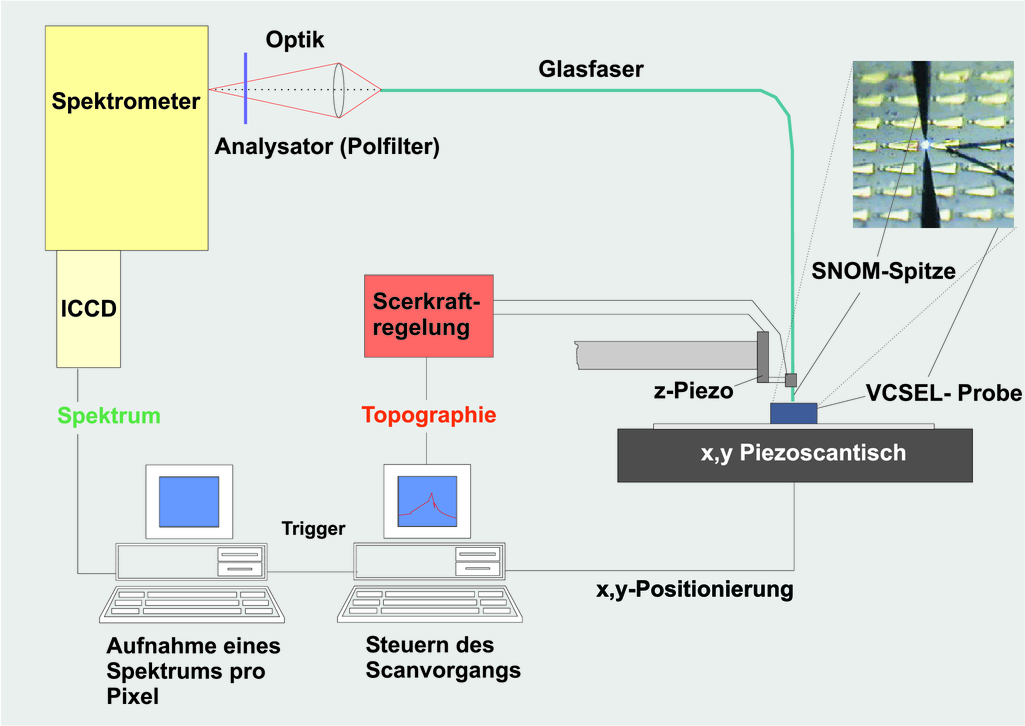
Aufbau der Nahfeld-Messeinrichtung für Modenverteilungen. (Zeichnung von Markus Fischer[Fis97]).
_____________________________________________________________________
_____________________________________________________________________

Nahaufnahme von Glasfaser-Nahfeldsonden. (Daten gemessen von Markus Fischer[Fis97]).
_____________________________________________________________________
_____________________________________________________________________
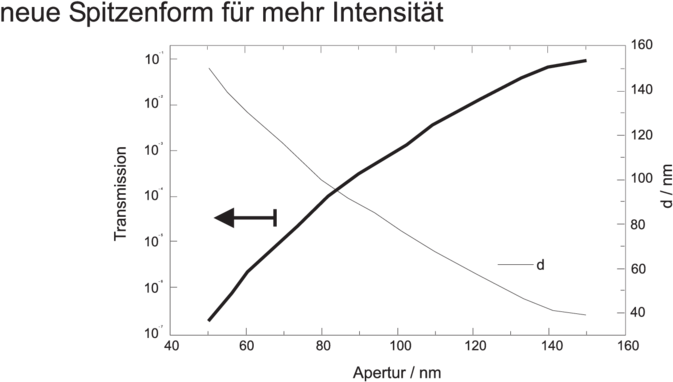
Transmission von Nahfeld-Glasfasersonden. (Schaubild gezeichnet von Markus Fischer[Fis97]).
_____________________________________________________________________
_____________________________________________________________________
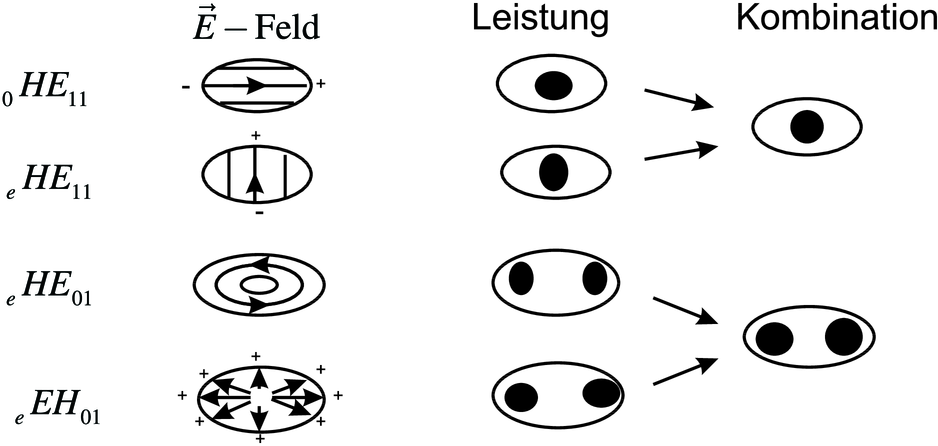
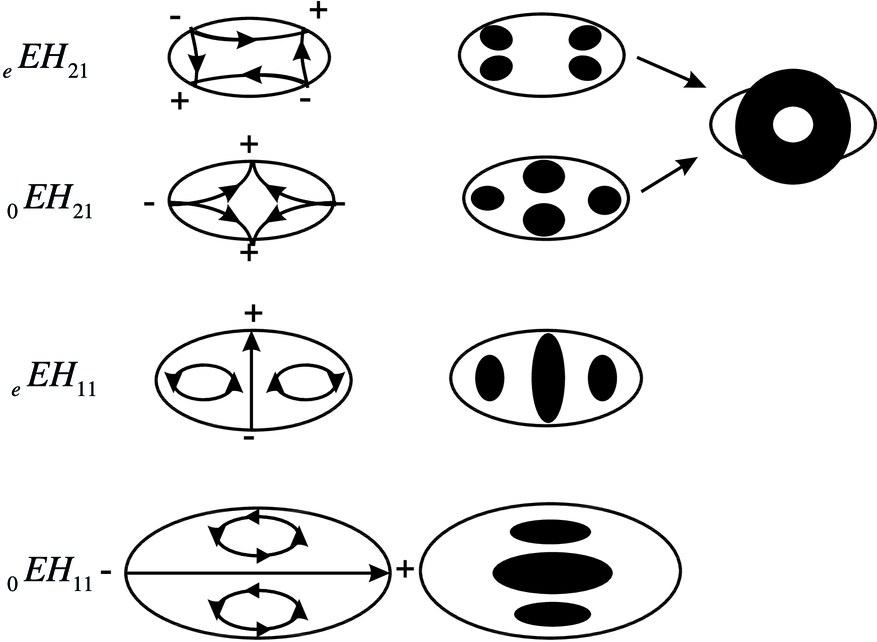
Wellenleitermoden für elliptische Wellenleiter. Links sind die Bezeichnungen, dann die Anordnung der elektrischen Felder und schliesslich die Intensitätsmuster gezeigt. (gezeichnet nach [Dyo95].)
_____________________________________________________________________
_____________________________________________________________________
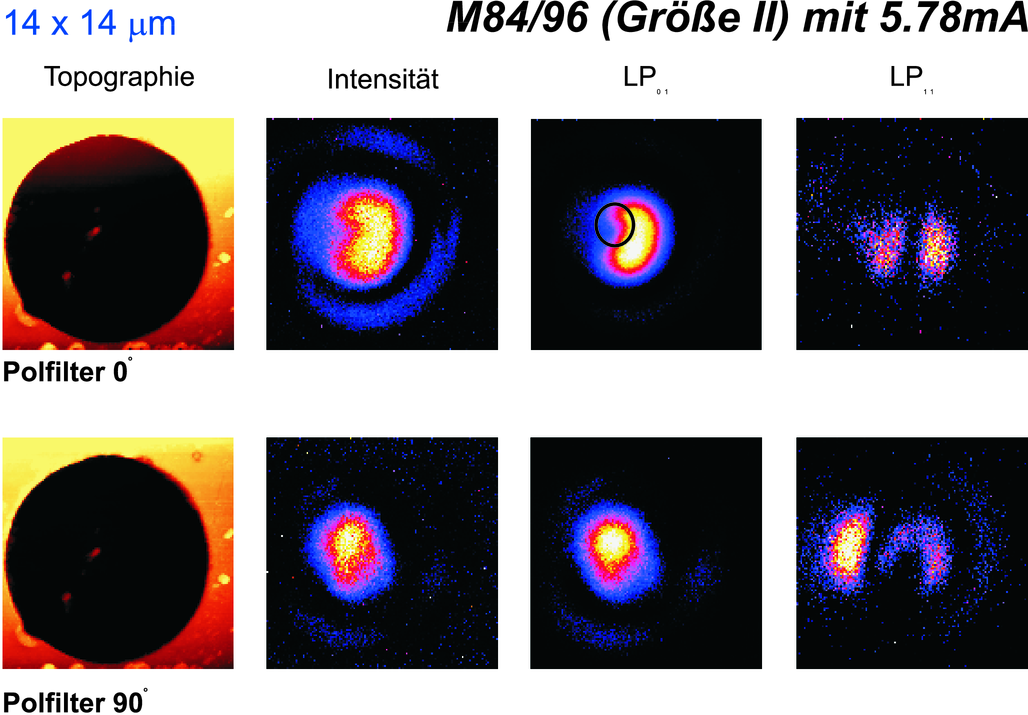
Diese Aufnahme zeigt Moden bei relativ geringen Strömen. Deshalb können nur die Grundmode sowie noch wenige Oberwellen anschwingen. Die Modenform wird durch die Verunreinigungen auf den Laserspiegeln (rechts sichtbar) hervorgerufen. In der Unteren Reihe ist der Analysator für die Polarisation um π∕2 gedreht worden. Die beiden Reihen zeigen also die beiden orthogonalen Polarisationszustände des Lichtes. (Daten gemessen von Markus Fischer[Fis97]).
_____________________________________________________________________
_____________________________________________________________________
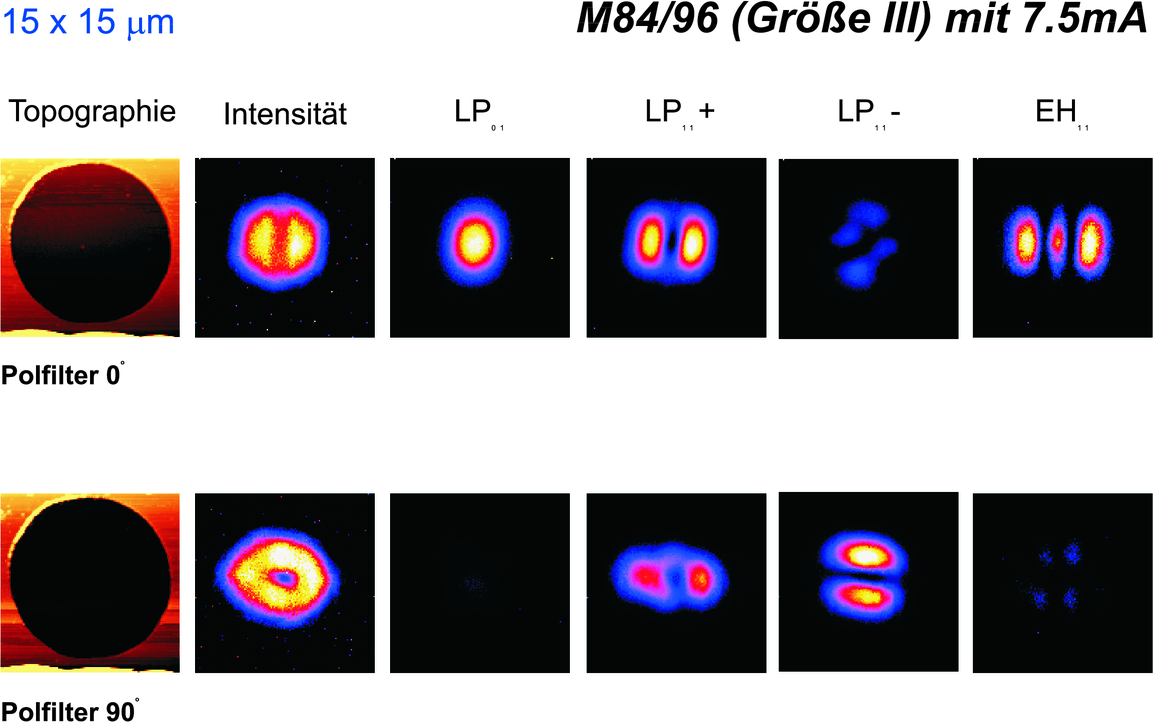
Bei ähnlichem Strom hängen die möglichen Moden auch vom Durchmesser des Resonators ab. Dieser Resonator ist grösser als der im vorherigen Bild. (Daten gemessen von Markus Fischer[Fis97]).
_____________________________________________________________________
_____________________________________________________________________
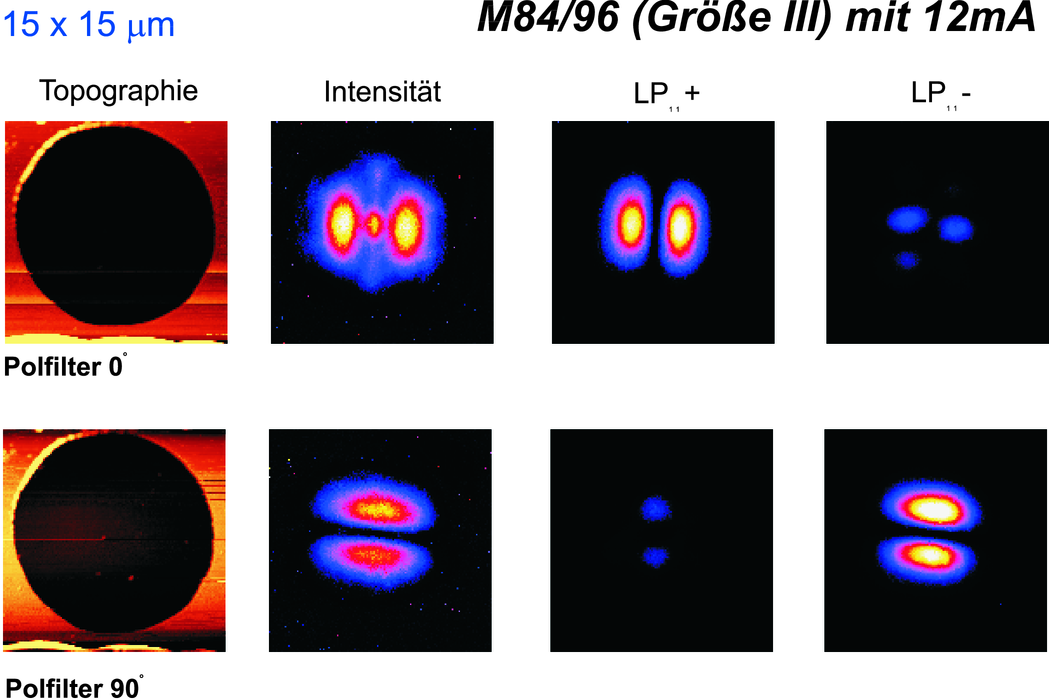
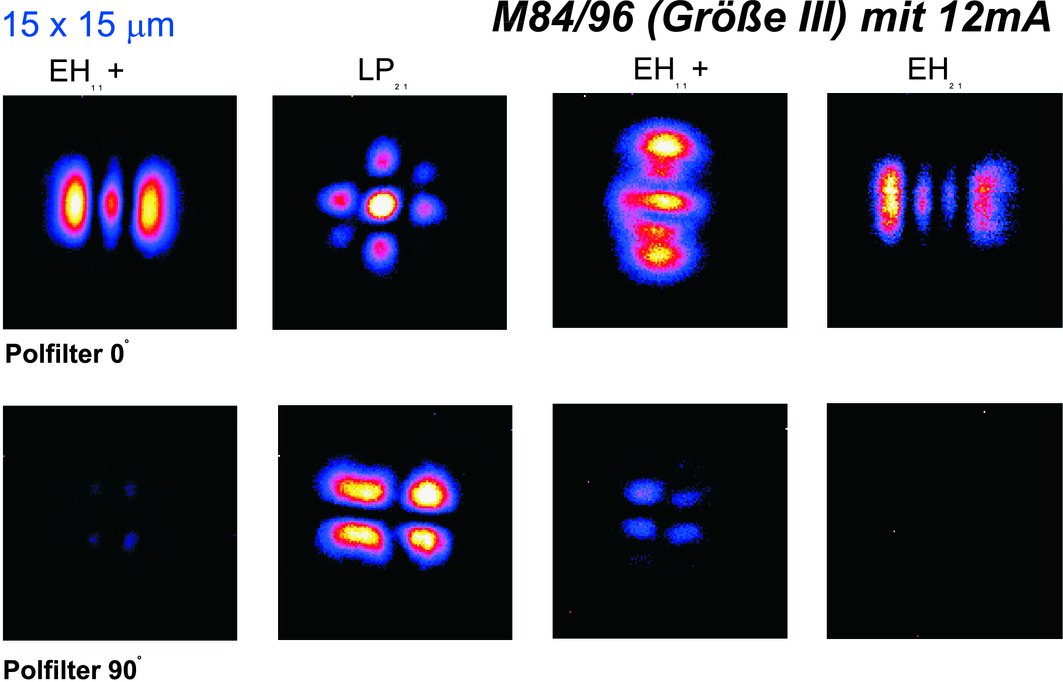
Hier ist der Strom bei gleicher Geometrie grösser als im vorherigen Bild. Entsprechend schwingen mehr Moden an. Beachten Sie, dass die Knotenlinien von Moden mit einer orthogonalen Polarisation auch orthogonal sind. (Daten gemessen von Markus Fischer[Fis97]).
_____________________________________________________________________
_____________________________________________________________________
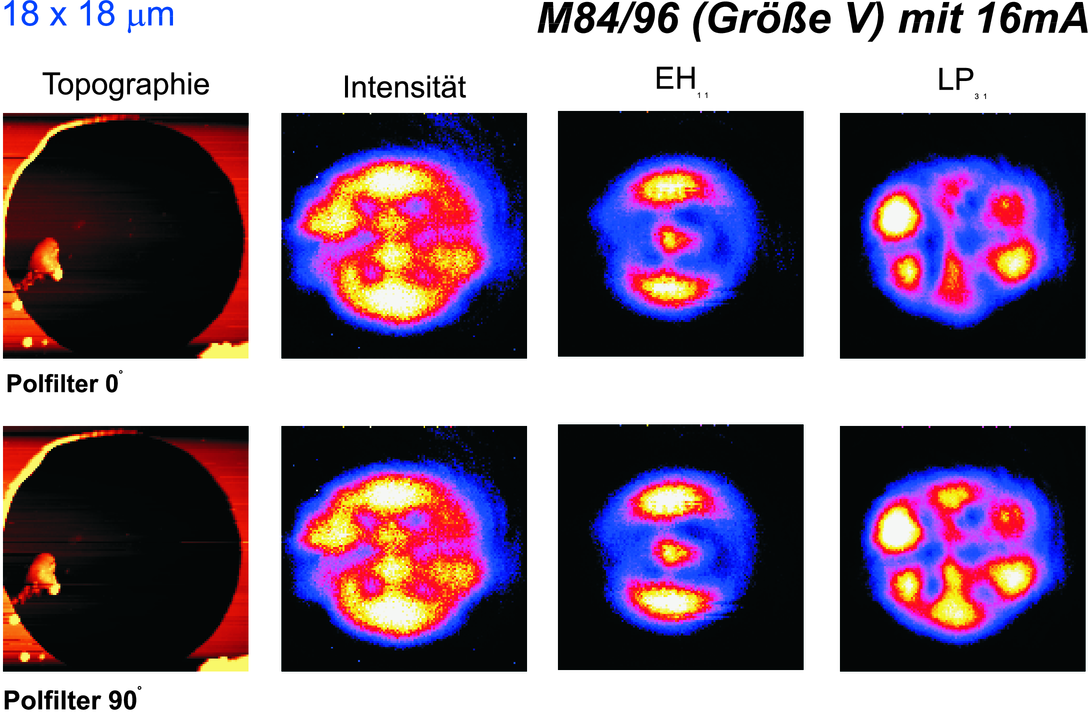
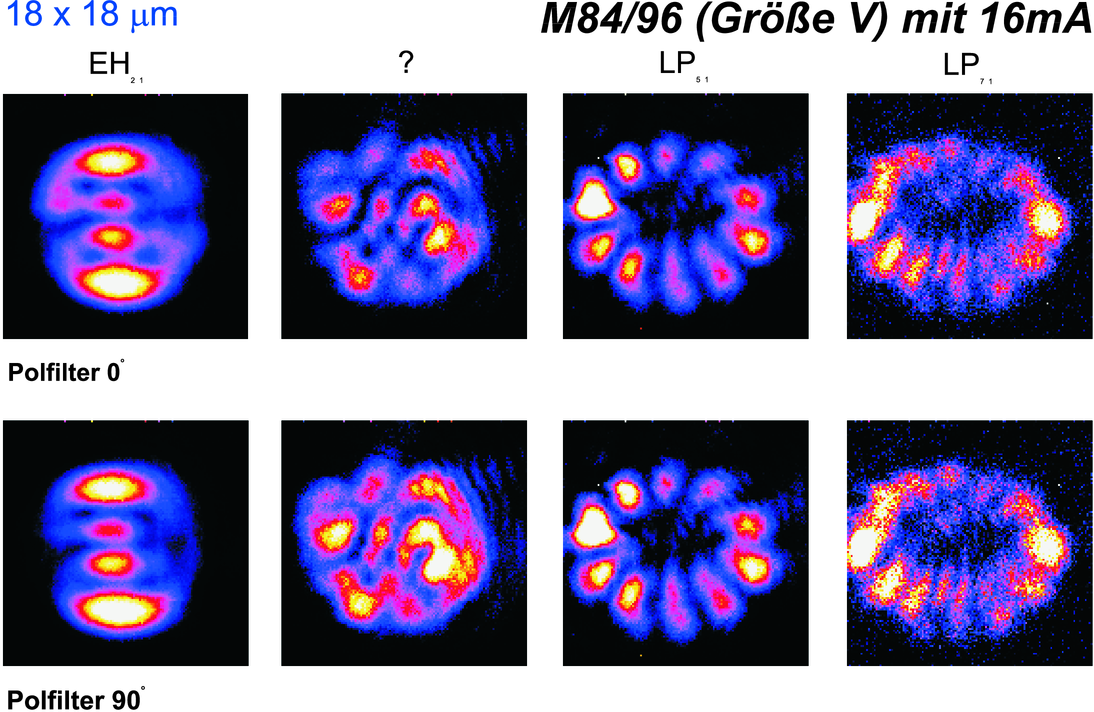
Dieser Laserresonator hat den grösseren Durchmesser als der vorherige. Da auch der Injektionsstrom grösser ist, schwingen hier sehr viele Moden an, die zum Teil auch nicht mehr identifiziert werden können. (Daten gemessen von Markus Fischer[Fis97]).
_____________________________________________________________________
_____________________________________________________________________
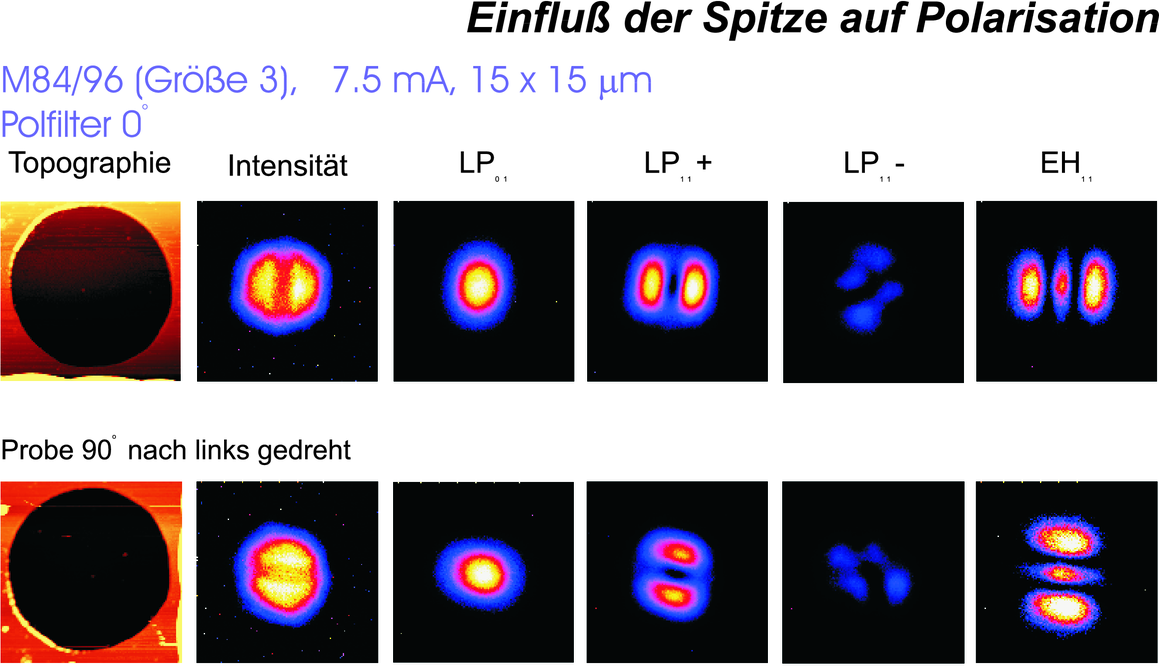
Hier wird gezeigt, dass die Sonde, hier ”Spitze” genannt, keinen Einfluss auf die Messung hat. (Daten gemessen von Markus Fischer[Fis97]).
_____________________________________________________________________
_____________________________________________________________________

Wie bei allen Messmethoden gibt es auch hier Artefakte. So führen hier Rückwirkungen auf den Laser zu einer optisch sonst nicht erklärbaren Streifenbildung. (Daten gemessen von Markus Fischer[Fis97]).
_____________________________________________________________________
Nach Yariv[Yar75, 118] genügen die Moden in rechteckförmigen Wellenleiter
![( ) ( )
E = E -ω0-H √2---x-- H √2---y---
ℓ,m 0 ω(z) ℓ ω (z) m ω(z)
[ 2 2 ]
× exp − ik x-+--y--− ikz + i(m + n + 1)η
2q(z)
ω ( √ -- x ) ( √ -- y )
= E0 --0-H ℓ 2----- Hm 2 -----
ω(z) ω (z) ω(z)
[ x2 + y2 x2 + y2 ]
× exp − --2-----− ik--------− ikz + i(m + n + 1 )η
ω (z) 2R (z )
(7.47)](op-2016-2017934x.png)
wobei Hℓ das Hermitsche Polynom ℓ-ten Grades ist und die anderen Grössen wie bei den Gaussschen Strahlen definiert sind.
 Lizenzinformationen
Lizenzinformationen