
Soweit bekannt ist, war der polnische Naturphilosoph Witelo aus Liegnitz bei Breslau/Schlesien (geboren um 1230, gestorben zwischen 1275 und 1314) der erste Forscher, der bemerkte, dass Lichtstrahlen nicht unendlich dünn werden können (Bemerkung im Buch von John Freely [Fre12, Fre15]). Diese experimentelle Beobachtung ist der erste bekannte experimentelle Hinweis auf die Wellennatur des Lichtes [Thu72, Wik26].
Dieses Kapitel beruht auf den in der Elektrizitätslehre abgeleiteten Wellengleichungen (2.1) oder (2.2)
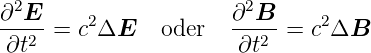 |
In diesem Abschnitt sollen die Eigenschaften von Licht, die auf der Wellennatur, also auf (2.1) oder (2.2), beruhen, diskutiert werden. Alle Lösungen hängen von einem skalaren parameter ab, der in den Gleichungen (2.6) und (2.7) eingeführten Phase.
Wir setzen also
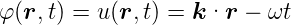 | (3.1) |
Dabei ist in kartesischen Koordinaten 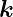 =
= 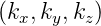 T der
Wellenvektor und
T der
Wellenvektor und 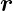 =
= 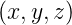 T der Beobachtungsort. Der
Wellenvektor ergibt sich aus
T der Beobachtungsort. Der
Wellenvektor ergibt sich aus 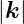 = 2π∕λ aus der Wellenlänge
λ, die Kreisfrequenz ω = 2πν = 2π∕T aus der Frequenz ν oder
aus der Periodendauer T = 1∕ν.
= 2π∕λ aus der Wellenlänge
λ, die Kreisfrequenz ω = 2πν = 2π∕T aus der Frequenz ν oder
aus der Periodendauer T = 1∕ν.
Damit sind zum Beispiel
| Versuch zur Vorlesung: | |
| Wellenmaschine (Versuchskarte SW-077) | |
_______________________________________________

Interferenz zweier Kreiswellen im Riffelsee auf der Riffelalp.
_____________________________________________________________________
Abbildung 3.1 zeigt die Interferenz von Kreiswellen auf der Wasseroberfläche.
__________________________________________________________________________

Detail aus Abbildung 3.1. Die grüne Linie liegt im Bereich, in dem zwei Wellen interferieren.
_____________________________________________________________________
_____________________________________________________________________
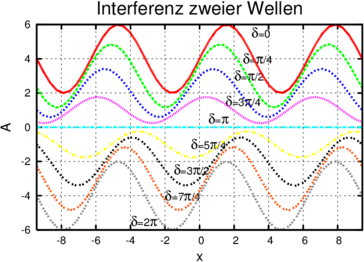
Interferenz zweier Wellen mit der gleichen Amplitude und der gleichen Frequenz und einer Phase, die von 0…2π variiert.
_____________________________________________________________________
Abbildung 3.1 zeigt schematisch, wie solche Wellen entlang der grünen Linie in Abbildung 3.1 interferieren könnten.
Zur Beschreibung diese in der Wellenwanne und im Riffelsee beobachteten Interferenz setzen wir zwei Wellen an, wobei wir hier nur die x-Komponente und skalare Amplituden betrachten
Die Phase der beiden Wellen unterscheidet sich dabei um δ, der Phasendifferenz. Wie immer ist nur der Real- oder der Imaginärteil messbar.
An einem bestimmten Ort zu verschiedenen Zeiten t1 und t2 ist die Differenz der Phasen durch
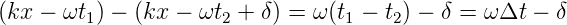 | (3.4) |
gegeben und unabhängig vom Ort. Zu einer bestimmten Zeit und an verschiedenen Orten x1 und x2 ist die Differenz der Phasen durch
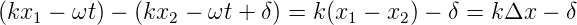 | (3.5) |
gegeben, unabhängig von der Zeit.
Beobachten können wir nur die Summe der beiden Wellen, also
Wir wenden die Additionstheoreme für die Winkelfunktionen an. Wir verwenden
und erhalten
Wenn beide Wellen die gleiche Amplitude haben Aus dieser Gleichung kann bei gleichen Amplituden (ΔA = 0) die folgende Tabelle abgeleitet werden.
___________________________________________________________________________
| Phase | resultierende Amplitude | Interferenz |
| 0 | 2A0 | konstruktiv |
| π∕2 | 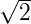 A0 A0 | |
| π | 0 | destruktiv |
| 3π∕2 | 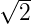 A0 A0 | |
| 2π | 2A0 | konstruktiv |
_____________________________________________________________________
Wenn ΔA > 0 ist, fehlt der Fall der kompletten destruktiven Interferenz.
 Lizenzinformationen
Lizenzinformationen